从概念到成品：用AssetStudio制作手游角色的全流程

原创于 2025-12-01 11:44:04 发布 · 501 阅读

CC 4.0 BY-SA版权

输入框内输入如下内容：

开发一个角色创建教程项目，逐步演示：1) 使用基础几何体构建角色轮廓 2) 添加细节雕刻 3) 创建UV贴图 4) 绘制基础材质 5) 设置骨骼和简单动画。要求包含分步指导、常见问题解决方案和优化技巧。输出为可交互的教程应用，支持用户跟随操作。

示例图片

最近尝试用AssetStudio完整制作了一个手游角色资产，从零开始到最终导出，整个过程既有趣又充满挑战。下面分享我的实战经验和踩坑总结，希望能帮到同样想学习游戏美术制作的朋友们。

角色制作的第一步是搭建基础模型。这里推荐从简单的几何体开始，比如用立方体构建躯干、圆柱体做四肢。关键要注意比例关系，手游角色通常采用Q版或卡通风格，头部比例可以适当放大。

有了基础轮廓后，就要添加让角色生动的细节。AssetStudio的雕刻工具可以很好地处理这个环节：

遇到细节丢失的问题时，记得检查细分层级是否足够。如果模型面数太高，可以先用低模雕刻再细分。

这是很多人容易卡住的环节。我的经验是：

示例图片

手游角色通常使用卡通着色风格。在AssetStudio中：

记得导出时选择手游常用的压缩格式，比如ETC2或ASTC。

要让角色动起来，需要：

最后导出为FBX格式时，记得勾选嵌入媒体选项。

整个流程下来，最大的体会是手游角色制作要特别注意性能优化。面数控制在1-2万，贴图分辨率根据设备适当调整。AssetStudio的工作流非常顺滑，特别是它的实时预览功能，能随时查看最终效果。

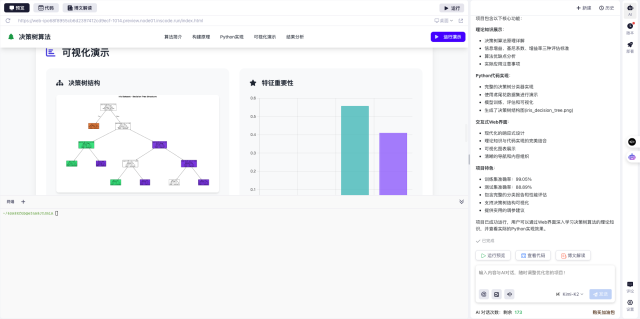
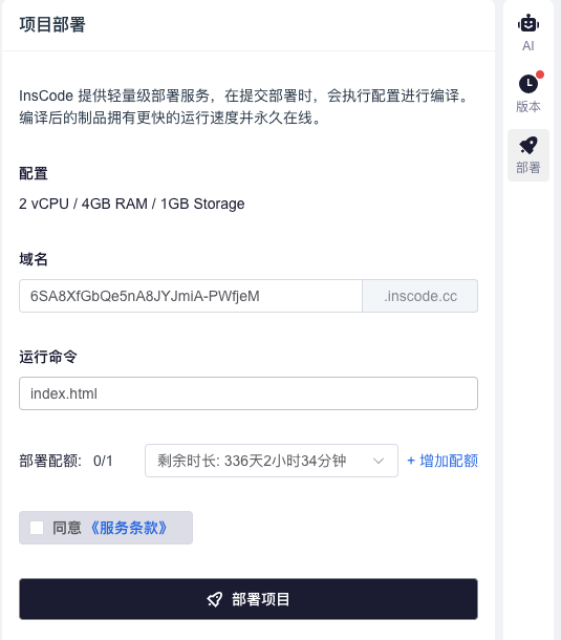
如果你想快速体验游戏开发，推荐试试InsCode(快马)平台。它的在线编辑器可以直接运行和测试游戏项目，还能一键部署查看实际效果。我测试时发现，从建模到部署的整个过程都能在一个平台完成，特别适合想快速验证创意的开发者。

示例图片

下次我准备尝试用这个流程制作一个完整的角色包，到时候再来分享更多细节技巧。

输入框内输入如下内容：

开发一个角色创建教程项目，逐步演示：1) 使用基础几何体构建角色轮廓 2) 添加细节雕刻 3) 创建UV贴图 4) 绘制基础材质 5) 设置骨骼和简单动画。要求包含分步指导、常见问题解决方案和优化技巧。输出为可交互的教程应用，支持用户跟随操作。

创作声明：本文部分内容由AI辅助生成（AIGC），仅供参考