洛谷P4568飞行路线（分层图最短路）

分层图最短路

• 题目 P4568飞行路线

做法1

• 题目说一共有k次免费乘坐机会。
• 我们可以假设每个点都有免费通向下一个点的一条路，建k+1层图。
  
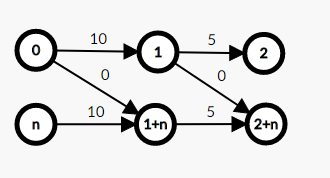
• （当然这里要建双向边）第一行是第一层图，第二行是第二层图（注：因为第一层有n个点，所以第二层要从n+0开始，避免重复）第一层表示不消耗免费次数，第二层表示消耗一次免费次数，以此类推，第 i 层表示消耗 i-1 次免费次数。
• 于是我们就可以通过比较起点0到终点 n , 2n , 3n，. . .，(k+1)*n 的最短路来找到消耗k次免费机会后的最短路，也就是最小花费。
• ans=min(dis[n],dis[2*n],dis[3*n],...,dis[(k+1)*n]);

举个例子

`

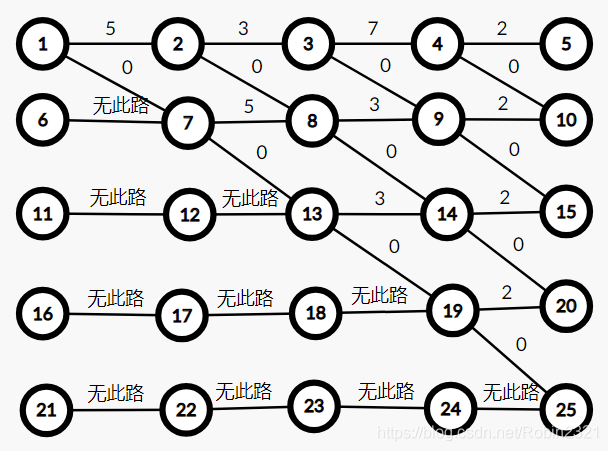
• dis[2]表示1到2的最短路,dis[5]表示1到5的最短路；
• dis[10]表示1到10的最短路，由图可以看出，有且只有经过了1条权值为0的边才能到10这个点，也就是说花费了1次免费机会；
• 同样，dis[15]表示1到15的最短路，由图可以看出，有且只有经过了2条权值为0的边才能到15这个点，也就是说花费了2次免费机会；
• 同理，dis[20]表示1到20的最短路，由图可以看出，有且只有经过了3条权值为0的边才能到20这个点，也就是说花费了3次免费机会；
• 以此类推，dis[25]表示1到25的最短路，由图可以看出，有且只有经过了4条权值为0的边才能到25这个点，也就是说花费了4次免费机会；
• 所以，显然，ans=min(dis[5],dis[10],dis[15],dis[20],dis[25]);（这里要看k是多少，比较k+1个数的大小）。

下面看代码

#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 900005//因为要建n*(k+1)个点 
#define maxm 90000005//因为有好多条边（当然我这里太大了点） 
#define inf 0x7fffffff
#define ri register int
using namespace std;
priority_queue<pair<int,int> >q;//骚操作 
int to[maxm];
int weight[maxm];
int next[maxm];
int head[maxn];
int dis[maxn];
int vis[maxn];
int n,m,K,s,t,cnt;
inline int read()//快读 
{
	ri x=0,f=1;
	char ch=getchar();
	while(ch>'9'||ch<'0') 
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
inline void add_edge(int u,int v,int w)//建边 
{
	to[cnt]=v;
	weight[cnt]=w;
	next[cnt]=head[u];
	head[u]=cnt;
	cnt++;
}
void Dijkstra(int s,int t)//这里和最短路一毛一样 
{
	for(ri i=0;i<=maxn;++i) dis[i]=inf;//每个点都要初始化 
	dis[s]=0;
	q.push(make_pair(-dis[s],s));
	while(q.size())
	{
		ri k=q.top().second;
		q.pop();
		if(vis[k]) continue;
		vis[k]=1;
		for(ri i=head[k];i!=-1;i=next[i])
		{
			ri v=to[i],w=weight[i];
			if(!vis[v]&&dis[k]+w<dis[v])
			{
				dis[v]=dis[k]+w;
				q.push(make_pair(-dis[v],v));
			}
		}
	}
}
int main()
{
	n=read(),m=read(),K=read();
	s=read(),t=read();
	memset(head,-1,sizeof(head));
	for(ri i=1,u,v,w;i<=m;++i)
	{
		u=read(),v=read(),w=read();
		for(ri j=0;j<=K;++j)
		{
			add_edge(u+n*j,v+n*j,w);//建当前层的图 
			add_edge(v+n*j,u+n*j,w);
			if(j!=K)//第K层没有下一层 
			{
				add_edge(u+n*j,v+n*(j+1),0);//建下一层的图 
				add_edge(v+n*j,u+n*(j+1),0);
			}
		}
	}
	Dijkstra(s,t);
	ri min=inf;
	for(ri i=0;i<=K;++i)
		if(dis[t+n*i]<min) min=dis[t+n*i];//找K+1层中最小的值 
	printf("%d",min);
	return 0;
}

• 看不懂我的代码的请看这里。

做法2

• dp思想，数组多开一维。
• dis[i][j]表示到第i个点用了j次免费机会的最短路。
• 同样，vis[i][j]用来判断到第i个点用了j次免费机会的情况是否出现过。
• 不使用免费机会dis[v][c]=min(dis[u][c]+w,dis[v][c]);
• 使用免费机会dis[v][c+1]=min(dis[v][c+1],dis[u][c]);

代码如下

#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 10005
#define maxm 100005
#define inf 0x7fffffff
#define ri register int
using namespace std;
priority_queue<pair< int,pair<int,int> > >q;//pair<int,int>看成一个整体
int to[maxm];
int weight[maxm];
int next[maxm];
int head[maxn];
int dis[maxn][11];//开二维
int vis[maxn][11];
int n,m,k,s,t,cnt;
inline int read()//快读
{
	ri x=0,f=1;
	char ch=getchar();
	while(ch>'9'||ch<'0')
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=x*10+ch-'0';
		ch=getchar();
	}
	return x*f;
}
inline void add_edge(int u,int v,int w)//建边
{
	++cnt;
	to[cnt]=v;
	weight[cnt]=w;
	next[cnt]=head[u];
	head[u]=cnt;
}
inline void Dijkstra(int s)
{
	for(ri i=0;i<maxn;++i)
		for(ri j=0;j<=10;++j)
			dis[i][j]=inf;//每个点都要初始化
	dis[s][0]=0;
	q.push(make_pair(-dis[s][0],make_pair(s,0)));
	//make_pair(s,0)和make_pair(0,s)是一样的
	while(q.size())
	{
		ri u=q.top().second.first;
		ri c=q.top().second.second;//c代表用了几次免费机会
		q.pop();
		if(vis[u][c]) continue;
		vis[u][c]=1;
		for(ri i=head[u];i;i=next[i])
		{
			ri v=to[i],w=weight[i];
			if(!vis[v][c]&&dis[u][c]+w<dis[v][c])
			{
				dis[v][c]=dis[u][c]+w;
				q.push(make_pair(-dis[v][c],make_pair(v,c)));
			}
			if(c<k&&!vis[v][c+1]&&dis[u][c]<dis[v][c+1])
			//c+1<=k，所以c要小于k
			{
				dis[v][c+1]=dis[u][c];
				q.push(make_pair(-dis[v][c+1],make_pair(v,c+1)));
			}
		}
	}
}
int main()
{
	n=read(),m=read(),k=read();
	s=read(),t=read();
	for(ri i=1,u,v,w;i<=m;++i)
	{
		u=read(),v=read(),w=read();
		add_edge(u,v,w);
		add_edge(v,u,w);
	}
	Dijkstra(s);
	ri min=inf;
	for(ri i=0;i<=k;++i)
		if(dis[t][i]<min) min=dis[t][i];
	printf("%d",min);
	return 0;
}

• 看不懂我的代码的请看这里。