第二周实习总结（7.22-7.26）

第二周实习总结

 Advance Office Password Breaker破解简单口令与复杂口令

1.简单口令

Range:0-65535

Average speed:4619095

Estimated time:2d 17h 26min

2.复杂口令

Range：0-65535

Average speed：4622574

Estimated time：2d 16h 5min

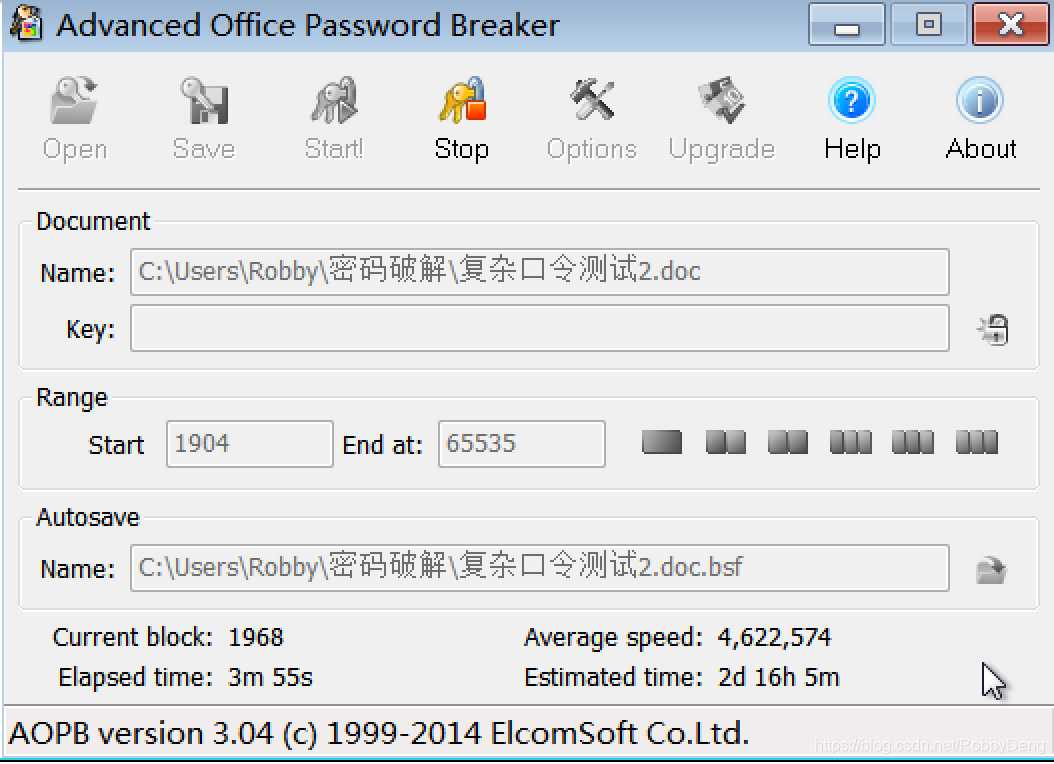
•   关于range的解释

The whole key range (1,099,511,627,776 as defined above) is divided into 65,536 blocks, with 16,777,216 keys in every block.

也就是说所有的key被划分成65536（2^16）个block，每个block中包含了16,777,216个key。可以选择range，比如全部、前一半、后一半、前三分之一等等。

 

• 在AOPB的instruction中我找到这样一段话：

Instead of testing all possible passwords, AOPB test all possible encryption keys. And once the key is found, it decrypts the document, so the password is no longer required to open it. Decryption is still not instant, but recovery time is very reasonable (usually, a few days). Moreover, this method provides 100% success rate regardless the password length. For example, if the speed is one million passwords per second even on old Pentium 4, the program will work about 305 hours or about 13 days – and this is maximum.

AOPB不是测试所有可能的密码，而是测试所有可能的加密密钥。一旦找到密钥，它就会解密文档，因此不再需要密码来打开它。解密仍然不是即时的，但恢复时间非常合理（通常是几天）。而且，无论密码长度如何，该方法都提供100％的成功率。例如，如果速度是每秒一百万个密码，即使在旧的奔腾4上也是如此，该程序将工作大约305小时或大约13天- 这是最大的。

所以AOPB破解密码与密码的长度与复杂程度无关，且时间较短。

Advance Office Password Recovery破解简单口令

使用AOPR破解简单口令速度不是很理想。以下为密码长度为8-12位，字符集位数字和小写字母的估计时间，供大家参考。

字符集	长度	速度（个/秒）	所需时间
数字+小写字母	8	523679	62.4d
	9	510806	6year 111d
	10	514027	225.5 year
	11	513447	8129 year
	12	524796	286308 year

使用彩虹表破解复杂口令

在我的机器上没有运行，但是之后会运行，时间大概是无论什么口令，20分钟内可以出结果。

使用Hashcat破解口令

这是一个不断尝试，不断失败的过程。

首先，我在win7系统的虚拟机下安装了hashcat，安装没有什么问题，我的建议是下载binaries版本的，直接有编译好的hashcat64.exe。

但是在运行的时候，会报下面的错误。

询问老师后，发现是不能再虚拟机上运行，然后我就换在我的本机上运行，但是mac上安装的hashcat的最高版本只有4.1.2。运行之后，又出现了下面的问题。

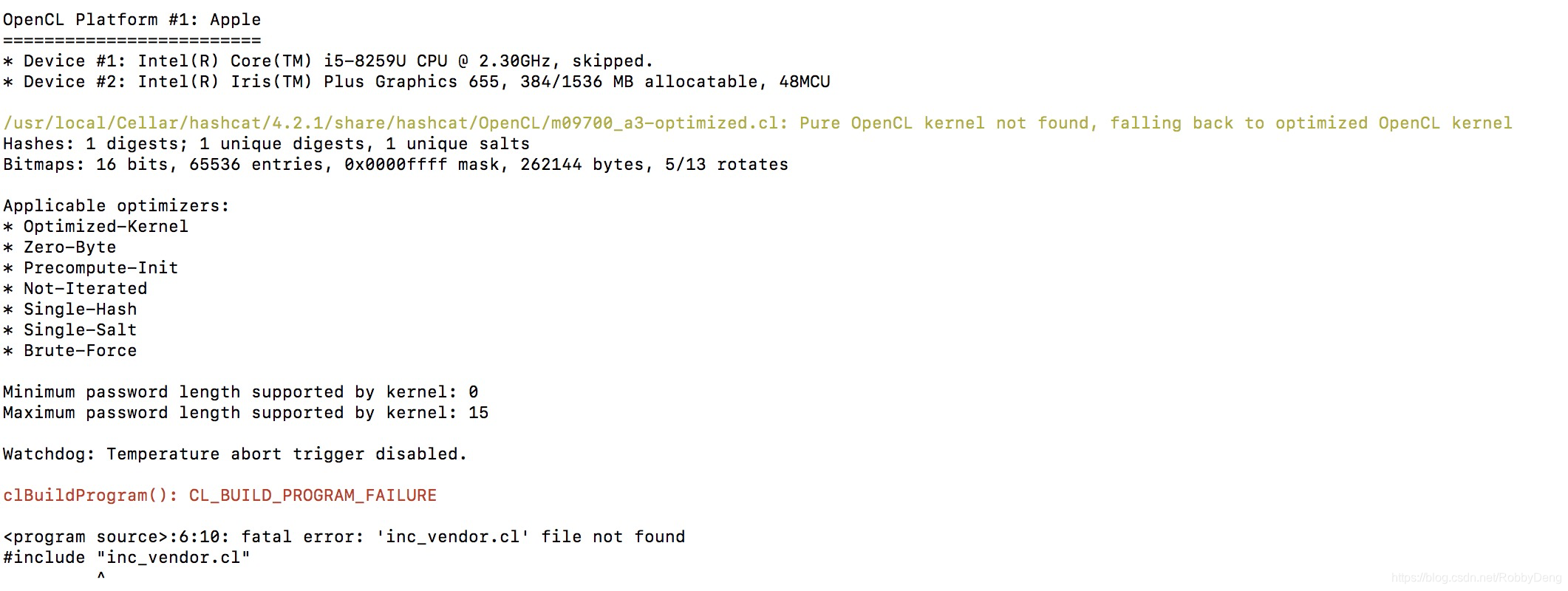
原因在于我的电脑没有CPU，于是采取了只使用CPU的方法，就是在命名后面加上--force。不幸的是，这样还是会失败。

网上关于mac的hashcat使用教程较少，只有一篇博客解决类似问题，但是它的电脑配置有GPU。

最终，我选择使用另一台win10系统的电脑，重新进行这个实验。

步骤如下：

1.为了简化命令行输入，我把简单口令测试文档重命名为1.doc，复杂口令测试文档重新命名为2.doc。

2.为了计算文档的hash值，我下载了john-1.8.0-jumbo-1.tar.gz，从中获取了office2john.py,并且将它放在待破解文档所在的文件夹下

3.运行office2john.py

office2john.py 1.doc>hash

4.处理hash文件，将无关的头尾删掉。(此处仅为示例)

5.破解Office加密Office版本对应的哈希类型

 

·  Office97-03(MD5+RC4,oldoffice$0,oldoffice$1)：-m 9700  

·  Office97-03($0/$1, MD5 + RC4, collider #1)：-m 9710 

·  Office97-03($0/$1, MD5 + RC4, collider #2)：-m 9720 

·  Office97-03($3/$4, SHA1 + RC4)：-m 9800 

·  Office97-03($3, SHA1 + RC4, collider #1)：-m9810 

·  Office97-03($3, SHA1 + RC4, collider #2)：-m9820 

·  Office2007：-m 9400  66  

·  Office2010：-m 9500 

·  Office2013：-m 9600

6.Hashcat中自定义破解含义值

• ?l = abcdefghijklmnopqrstuvwxyz，代表小写字母。
• ?u = ABCDEFGHIJKLMNOPQRSTUVWXYZ，代表大写字母。
• ?d = 0123456789，代表数字。
• ?s = !"#$%&'()*+,-./:;<=>?@[\]^_`{|}~，代表特殊字符。
• ?a = ?l?u?d?s，大小写数字及特殊字符的组合。
• ?b = 0x00 - 0xff

7.使用hashcat进行破解

//自定义破解密码长度为8，全部为数字的情况
hashcat64.exe -m 9700 hash -a 3 ?d?d?d?d?d?d?d?d -w 3 -O

 

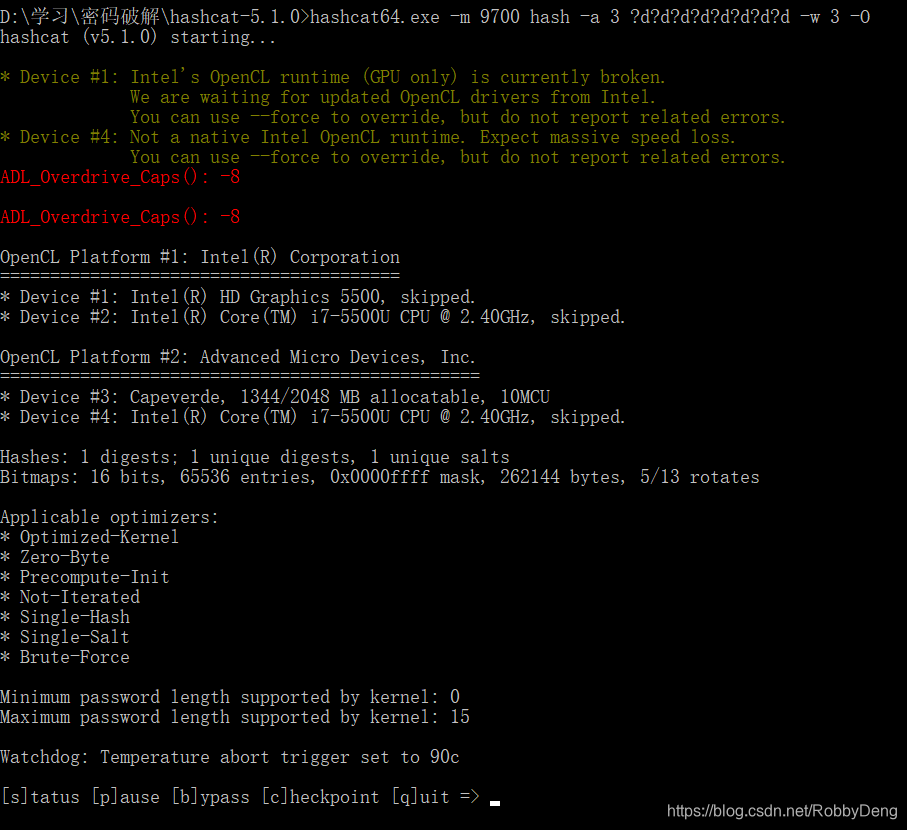
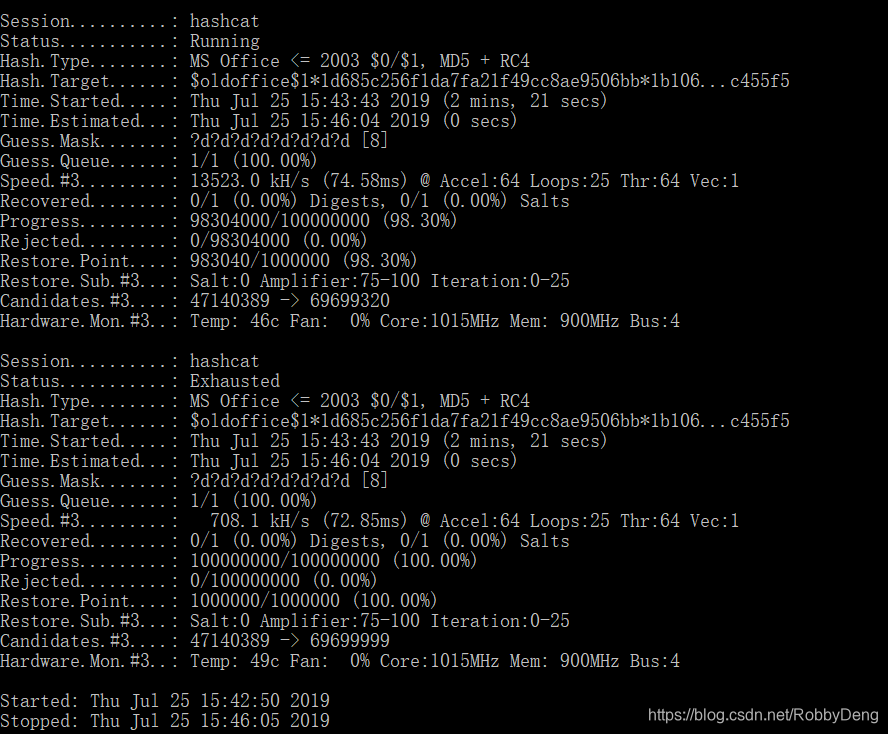
至此，虽然没有破解出密码，但是hashcat总算可以成功使用了。

接下来，开始进行复杂口令的破解，提示是中国人名+3位数字。我的想法是先制作出符合要求的字典，然后使用hashcat结合字典进行破解。那么接下来，就是字典是如何生成的。

我在网上找到两款字典生成器，分别进行实验，目前还没有在中国人名后加入数字。我还希望找到一款字典生成器，可以在字典后追加数字。

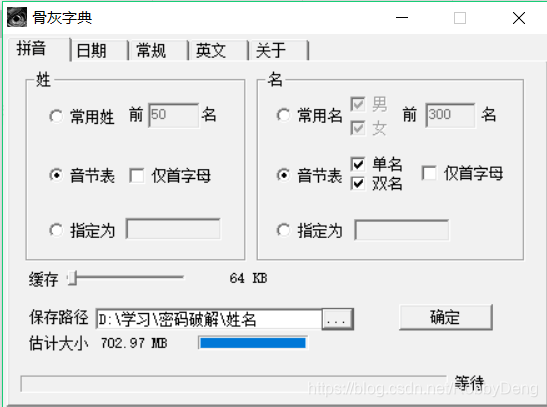
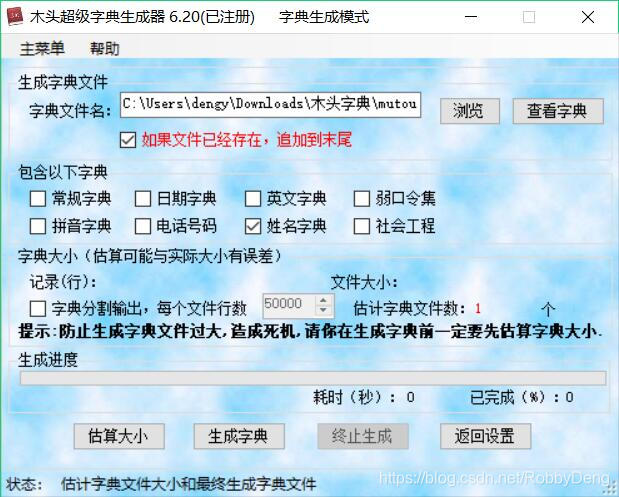
以上就是我本周的实习进度，我发现目前的问题总是出在不能很好的使用软件，时间大部分都花在解决一个软件能不能很好的运行在自己的机器上面了，之后的实习过程，我会多和老师沟通，希望可以少花些时间在这些问题上，但是踩进坑里也不是什么坏事，希望我的教训可以为其他人节约时间。