剑指offer #10- I 斐波那契数列

最新推荐文章于 2023-04-13 20:25:04 发布

原创最新推荐文章于 2023-04-13 20:25:04 发布 · 140 阅读

0 ·

CC 4.0 BY-SA版权

剑指offer刷题记录专栏收录该内容

9 篇文章

订阅专栏

本文探讨了计算斐波那契数列的多种方法，包括递归和动态规划，并详细解释了如何避免重复计算，提高算法效率。文章最后提供了一种优化后的动态规划解决方案，能够有效处理大数值的计算。

题目描述

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

题解

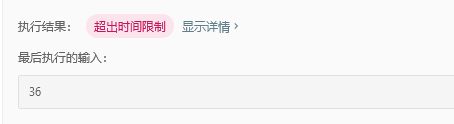
首先考虑递归，但因为存在大量重复计算，时间超出限制。

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return 1
        return self.fib(n-1) + self.fib(n-2) % 1000000007

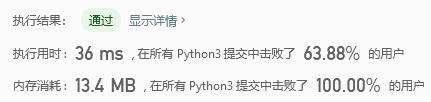
在这里插入图片描述
动态规划方法

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:    # 处理特殊输入
            return 0
        if n == 1:
            return 1
      
        # r = [0] * (n+1)         
        # r[1] = 1
        # for i in range(2,n+1):
        #     r[i] = r[i-1] + r[i-2]
        # return r[n] % 1000000007
		# 最初是创建一个列表来存储前面计算的值，但事实上计算n时只有n-1和n-2两个值需要保留，有如下代码
      
        r_0 = 0
        r_1 = 1
        for i in range(2,n+1):
            r_i = r_1 + r_0
            r_0 = r_1
            r_1 = r_i
        return r_i % 1000000007