P8692 [蓝桥杯 2019 国 C] 数正方形 O(n)优化到O(1) 题解及自出拓展题分享

前言

本人在教学过程中出过一道和本题类似，但是要比本题难度略高的一道同类题目，放在末尾，有需要的小伙伴可以自行挑战一下。

P8692 [蓝桥杯 2019 国 C] 数正方形

题目传送门

题目描述

在一个 $N\times N$ 的点阵上，取其中 $4$ 个点恰好组成一个正方形的 $4$ 个顶点，一共有多少种不同的取法？

由于结果可能非常大，你只需要输出模 $10^9+7$ 的余数。

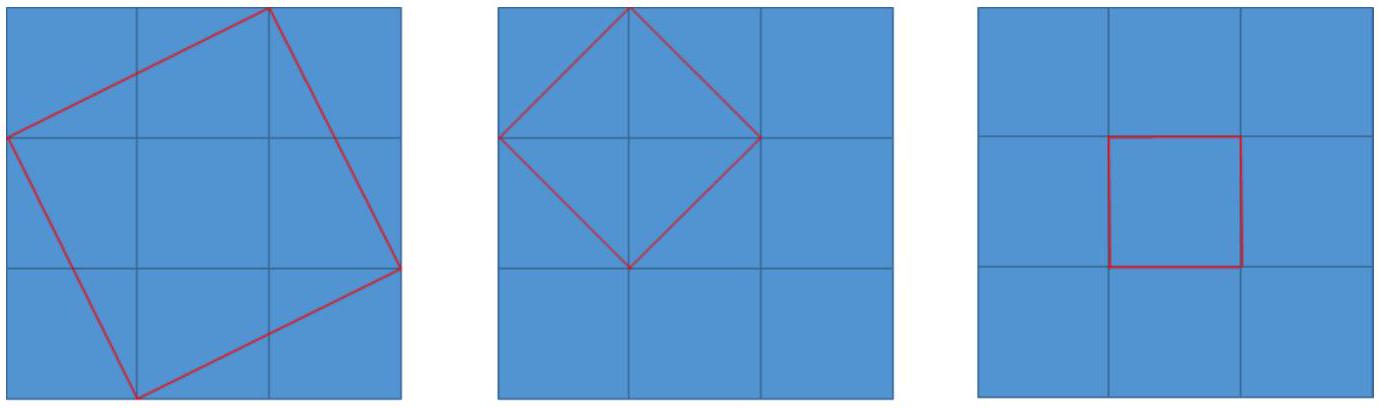
如上图所示的正方形都是合法的。

输入格式

输入包含一个整数 $N$。

输出格式

输出一个整数代表答案。

输入输出样例 #1

输入 #1

4

输出 #1

20

说明/提示

对于所有评测用例，$2\le N\le 10^6$。

思路分析

对于一个 $n\times n$ 的点阵，其实可以看做为一个边长为 $(n-1)\times (n-1)$ 的矩阵，所以最大的正方形边长为 $n-1$。

正方形的形态共两种，正正方形，斜正方形
斜正方形暂且考虑四个顶点全部坐落在最大正方形边长上的情况，虽然存在斜正方形坐落在大正方形的内部，但是我们可以将其转化为边长更小的正方形坐落在最大边长的子情况讨论。

设 $f(5)$ 表示边长为 $5$ 的正方形个数，所以下图的情况可以转化为求第一个 $f(4)$ 正方形的子情况。该正方形的四个顶点都是坐落于 $f(4)$ 正方形的最外围边长上的。

下图中标黄色的部分的三角形不难证明是均是互相全等的三角形。

所以我们在考虑坐落于最大边的斜正方形时，直接考虑距离四角的位置即可，下图的红框正方形既可以理解为距离四角位置为 $1$，也可以理解为距离四角位置为 $3$，不难发现，斜正方形有对称性。

若斜正方形的顶点坐落在最大边上距离四角的距离为 $0$，就转化成了正正方形，如下图所示：

所以我们可以将正正方形，和斜正方形统一讨论，即 距离最大边四个角的距离。

所以设最大边边长为 $k$， $k\in [1,n-1]$，设在最大边边长上，选取点距四个角的距离为 $d$，那么有$0\le d\le k-1$，共有 $k-1-0+1=k$ 种情况可选，即边长为 $k$ 的正方形，顶点坐落于最大边的正方形共 $k$ 个。

设边长为 $i,i\in [1,n)$ 在最大为 $n\times n$ 的正方形内共有 $(n-i)\times (n-i)$ 个边长为 $i$ 的正方形，每个正方形内根据上述推导共有 $i-1-0+1=i$ 种四个顶点坐落在 $i$ 边长上的正方形，所以根据乘法原理，我们可以推出：
$$f(n)=\sum _{i=1}^{n-1}i\times (n-i{)}^2$$

这样我们就有了本题的 $O(n)$ 复杂度的算法。

代码块

#include <bits/stdc++.h>
using namespace std;
const int p = 1e9 + 7;
long long n, ans;
int main() {
	cin >> n;
	for (long long i = 1; i < n; i++) {
		ans = (ans + i * (n - i) % p * (n - i)) % p;
	}
	cout << ans;
	return 0;
}

优化

观察 $f(n)={\sum }_{i=1}^{n-1}i\times (n-i{)}^2$，可以尝试对该公式进行化简去 ${\sum }_{}^{}$ 符号，转化成 $O(1)$ 的数学公式。

以下是公式变换过程：
$$\begin{array}{rl}f(n)& =\sum _{i=1}^{n-1}i\times (n-i{)}^2\\ & =\sum _{i=1}^{n-1}i\times (n^2-2in+i^2)\\ & =\sum _{i=1}^{n-1}i{n}^2-2i^{2}n+i^3\\ & =\sum _{i=1}^{n-1}i{n}^2-\sum _{i=1}^{n-1}2i^{2}n+\sum _{i=1}^{n-1}{i}^3\\ & =n^2\sum _{i=1}^{n-1}i-2n\sum _{i=1}^{n-1}{i}^2+\sum _{i=1}^{n-1}{i}^3\end{array}$$

不难发现，公式中出现了高斯公式，平方和公式和立方和公式。
已知：
$$\begin{array}{rl}& \sum _{i=1}^{n}i=\frac{n\times (n+1)}{2}\\ & \sum _{i=1}^n{i}^2=\frac{n(n+1)(2n+1)}{6}\\ & \sum _{i=1}^n{i}^3={\left[\frac{n\times (n+1)}{2}\right]}^2\end{array}$$

所以对上式进行化简：
$$\begin{array}{rl}f(n)& =n^2\sum _{i=1}^{n-1}i-2n\sum _{i=1}^{n-1}{i}^2+\sum _{i=1}^{n-1}{i}^3\\ & =n^2\times \frac{(n-1)\times n}{2}-2n\times \frac{(n-1)\times n\times (2n-1)}{6}+{\left[\frac{(n-1)\times n}{2}\right]}^2\\ & =\frac{n^3(n-1)}{2}-\frac{n^2(n-1)(2n-1)}{3}+\frac{n^2(n-1{)}^2}{4}\\ & =\frac{6n^3(n-1)}{12}-\frac{4n^2(n-1)(2n-1)}{12}+\frac{3n^2(n-1{)}^2}{12}\\ & =\frac{6n^4-6n^3}{12}-\frac{(4n^3-4n^2)(2n-1)}{12}+\frac{3n^2(n^2-2n+1)}{12}\\ & =\frac{6n^4-6n^3-8n^4+4n^3+8n^3-4n^2+3n^4-6n^3+3n^2}{12}\\ & =\frac{(6-8+3)n^4+(-6+4+8-6)n^3+(-4+3)n^2}{12}\\ & =\frac{n^4-n^2}{12}=\frac{n^2(n+1)(n-1)}{12}\end{array}$$

因为本题需要计算的是 $f(n)\%1000000007$ 后的结果，所以通过最终推出的 $O(1)$ 公式不难看出，本题存在了除后取模的问题，所以考虑计算 $12^{-1}$，即 $12\times x\equiv 1(\mathrm{mod}1000000007)$，因为 $1e9+7$ 是一个通用质数，考虑费马小定理，即 $12^{-1}\equiv 12^{1000000007-2}(\mathrm{mod}1e9+7)$，通过快速幂代码快速计算可得 $12^{-1}=83333334$。

所以最终得出 $O(1)$ 公式为：
$$f(n)=n^2(n+1)(n-1)\times 83333334\%mod。$$

代码块

#include <bits/stdc++.h>
using namespace std;
const int p = 1e9 + 7;
long long n;
int main() {
	cin >> n;
	cout << n * n % p * (n + 1) % p * (n - 1) % p * 83333334 % p;
	return 0;
}

本题的数据范围是可以继续提高到$10^9$的（误）。

三角形晶格传送门
本题的满分是$O(1)$，$10^9$的数据，需要考虑逆元，推导过程因为是三角形涉及正逆三角形，所以和 $n$ 的奇偶性相关，比本题略难