【新手Java】14.递归Recursion

系列的最后一篇了，最最最基础的Java到此为止
不过，目前所讲的只是Java的冰山一角，到此也只是能简单地用用Java罢了
不过，学习总是永无止境的，对吧

【介绍】
Java的一个方法可以调用它自己，Java和所有编程语言都可以支持这种情况，我们把它叫做递归Recursion
递归方法是一种调用自身的方法

那么使用递归方法是是怎么样的呢，让我们看看下面这段代码

（由于复制粘贴代码还要考虑排版，这里就上图了）
结果是程序会一直在调用这个方法，直到内存不足而停止（无限套娃）

【概念】
方法反复调用自身的概念称为递归
方法会不断调用自身，直到达到某些停止条件为止，有点像循环语句

在没有停止条件的情况下，程序将循环运行，直到计算机（Java虚拟机）内存不足（拒绝分配更多的内存）为止

虽然递归可能显得浪费甚至效率低下，但它在计算机科学和数学中是一个非常重要的概念
递归更像是一种思想，我们需要打破原有的“迭代”的思维定势（for,while）
为了帮助可视化“递归”，我们将使用一个称为堆栈 Stack的通用概念

堆栈基本上像自助餐厅中的托盘容器一样工作。它只有两个操作：
Push:你可以把某个东西压到栈上
Pop:你可以从堆栈的顶部弹出一些东西
First In Last Off
通过下面这张图感受一下

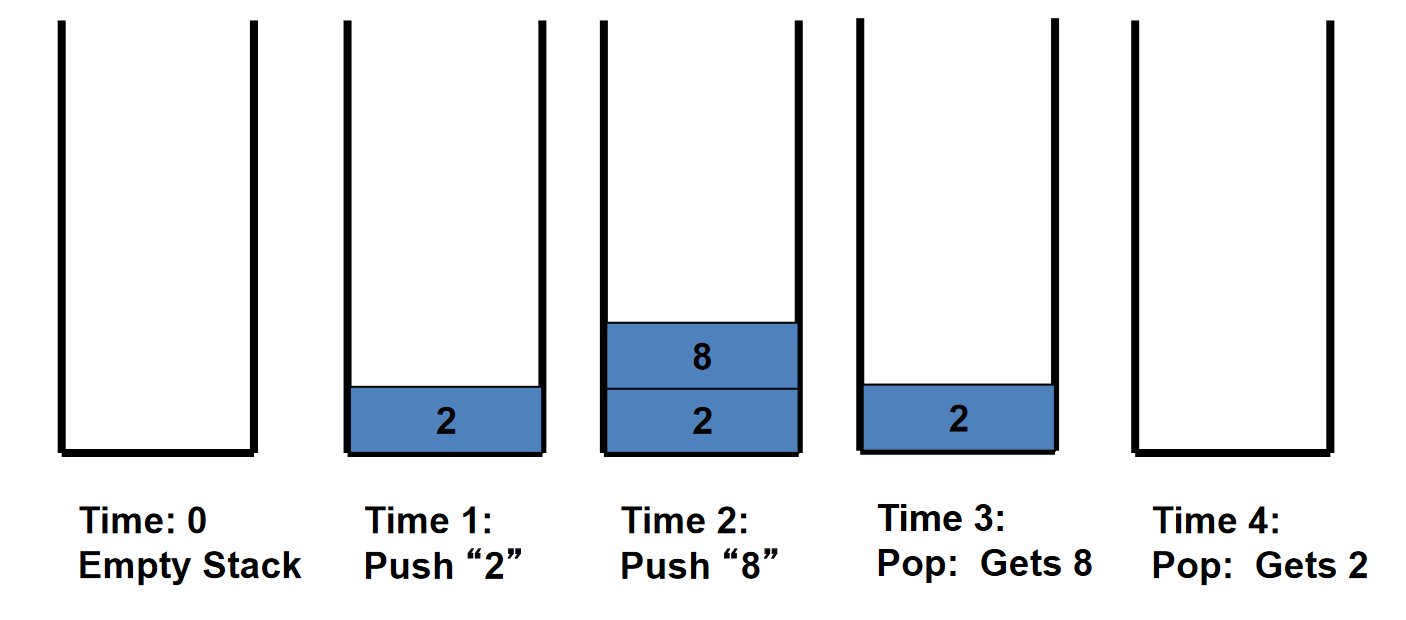
有的人说这就像弹匣一样，拉出来装Push然后从第一发开始射击Pop

【堆栈和方法 Stacks and Methods】
当你运行一个程序时，计算机会为你创建一个堆栈
每次调用方法时，该方法都会放在堆栈的顶部
当方法返回或退出时，该方法将从堆栈中弹出

【堆栈和递归 Stacks and Recursion】
每次调用方法时，都将该方法推入堆栈
每次方法返回或退出时，都将方法弹出堆栈
如果一个方法递归地调用自己，您只需将该方法的另一个副本压入堆栈
对于下面的这个简单程序：

public class Recursion1V0{
public static void main (String args[]) {
      count(0);
      System.out.println();
}
public static void count (int index) {
      System.out.print(index);
      if (index < 2) count(index+1);
}
}

我们将这个过程可视化之后便是这样

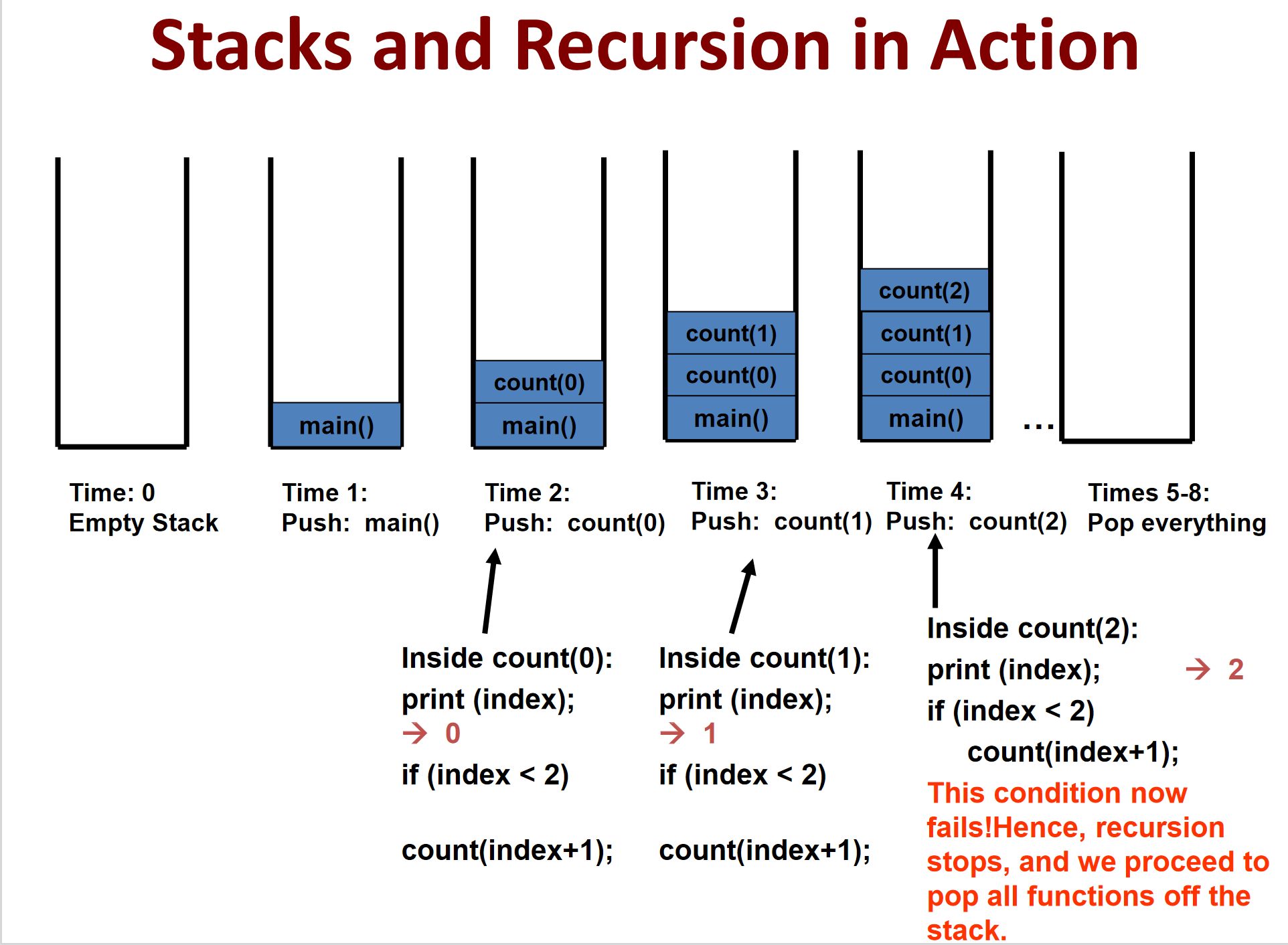
如果我们把代码改成

public class Recursion1V0{
public static void main (String args[]) {
      count(0);
      System.out.println();
}
public static void count (int index) {
      
      if (index < 2) count(index+1);
      System.out.print(index);  //注意这里！
}
}  

此时的输出是2 1 0 为什么呢，我们回忆一下堆栈的Push和Pop，就知道为什么了（FirstIn,LastOff）
我们需要一个方法执行结束（return好了），再执行接下来的操作
count(0)到count(1)到count(2)，结束执行，随后执行System.out.print(index)，分别打印210

【两种类型的递归】
1.直接递归 Direct recursion
方法直接包含对自身的引用或调用
2.间接递归 Indirect Recursion
一个方法调用另一个方法，该方法最终调用原始方法（比如A方法调用B方法，B方法调用A方法）

递归计算通过使用相同问题的解决方案来解决问题，但是具有更简单的值。我们称此为递归步骤 recursive step
为了使递归终止或停止，还必须有最简单值的特殊情况,我们称之为基本情况base case/anchor case/stopping condition
基本情况是为输入参数的一个或多个已知值指定方法值的情况

递归步骤(或归纳步骤)是根据先前定义的值定义对参数的当前值所采取的操作
为了执行递归，我们必须考虑以下两个方面
1.如何解决最简单的问题
2.给定一个更复杂的问题实例，如何使其更像最简单的实例？即如何使它更接近问题的最简单实例（使其像基本情况一样）？

【三步使用递归 Three Steps to Recursive Success 】

动手试试，我们写一个程序来检测字符串是否是回文（比如NAVAN）

1.减少 Reduction ——使问题变小
可以直接检测首尾的字符，如果它们是相同的，那么我们就删除它们（如果一开始就是回文如NAVAN，那么删除后得到的部分也是回文AVA）

2.基本情况 Base Cases ——处理简单的值，关键是找到最简单的情况的解决方案
比如有下面几个情况
1.最后没有字符了——是回文
2.最后剩下一个字符——是回文
3.最后剩下两个字符且二者不是同一个字符——不是回文

3.执行 Implement ——结合基本情况与步骤

【递归：阶乘】
1.寻找基本情况
对于阶乘而言，最基本的情况就是0！和1！，二者的结果都是1
我们不妨现在方法中写下这个情况，帮助我们跳出递归

if(i<=1){
return 1 ;
}

接下来，如果不是1或0，则进行阶乘运算

public static int Factorial (int i){
    if(i<=1){
    return 1 ;
    }else {
     return (i*Factorial(i - 1)) ;   
  }
}

思路很简单，我们从n开始放入，计算n！就需要（n-1）!，计算(n-1)!需要(n-2)!，以此递推到1！
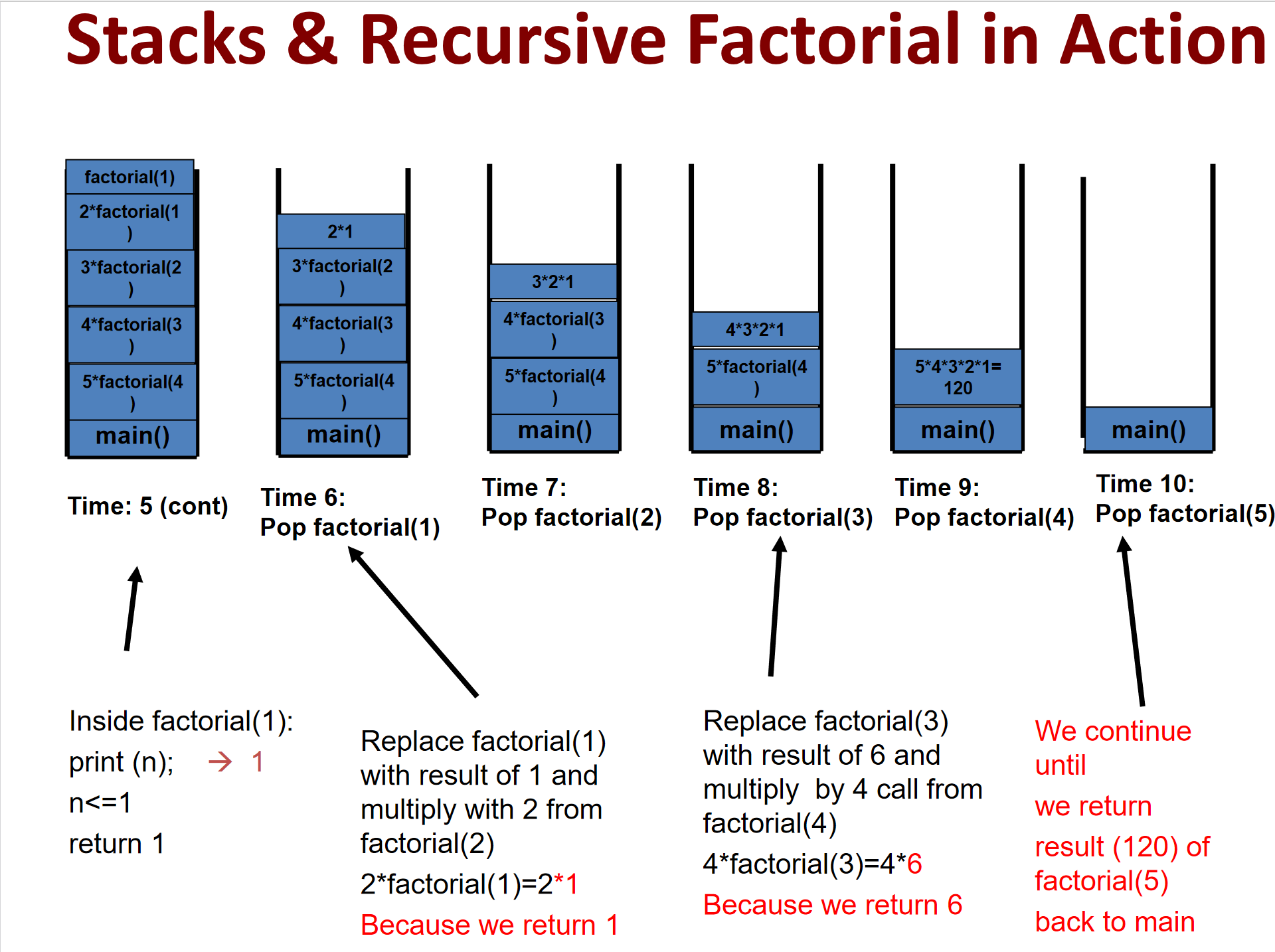
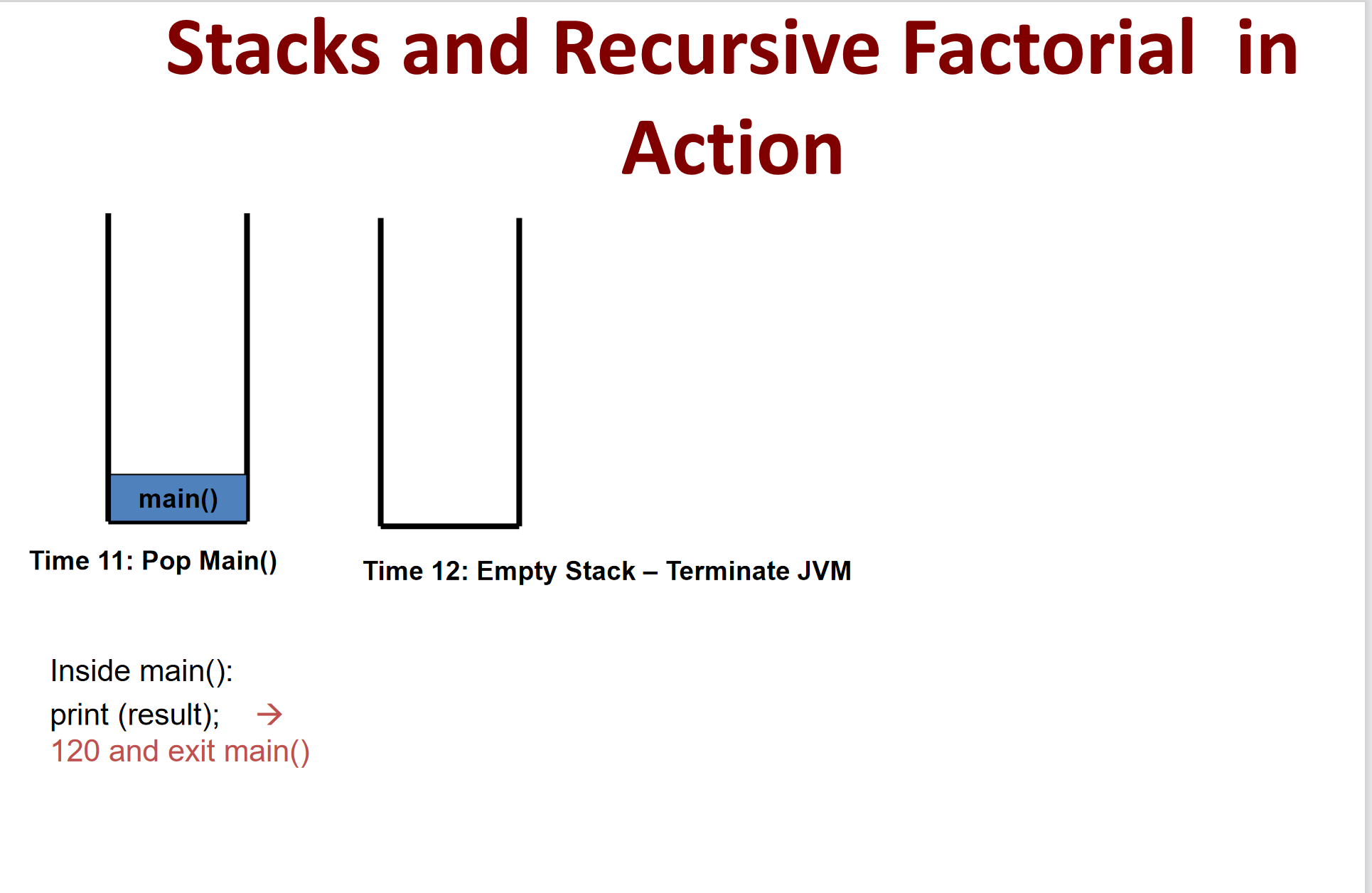
下面是对于这次操作的栈的示意图（以5为例）
建立堆栈（递归的过程）

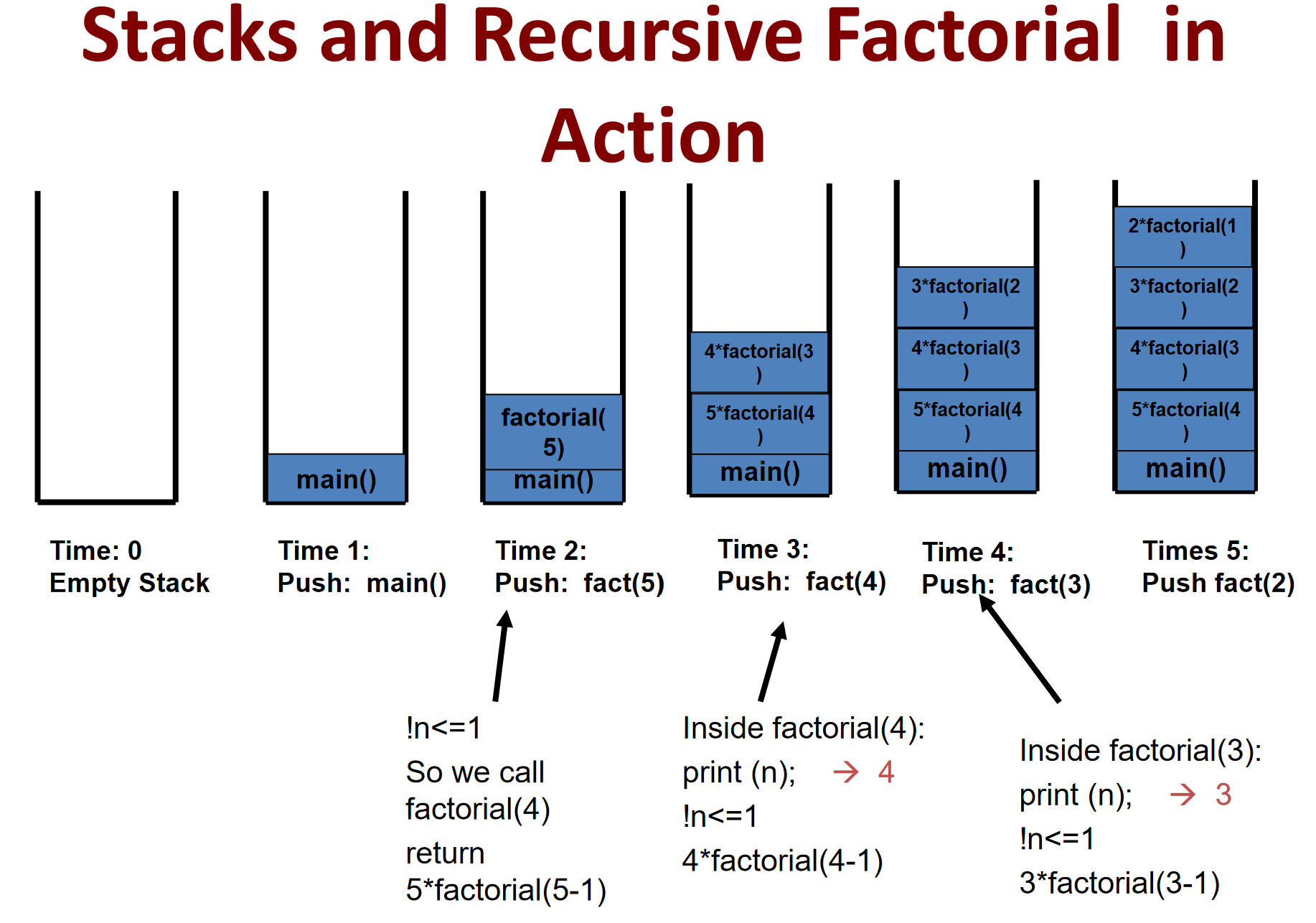
开始执行的时候，是从Factoria(1)逐级返回，最终得到5*4!即返回的过程

【递归：三角数】
三角数就像是加法的“阶乘”,必然1+2+3+4…
首先还是先寻找最初始的情况，显然那就是1了
和阶乘一样，我们也利用“堆栈——返回”的操作来进行三角数的计算
我们观察发现：出现一个模式即 T（n）= T（n –1）+ n 这种模式将有助于对三角数程序的递归进行程序编写。

public static int TrianNum(int i){
    if(i<=1){
    return 1 ;
    }else {
     return (i+TrianNum(i - 1)) ;   
  }
}

【斐波纳契数列 Fibonacci Numbers】
斐波那契数列：前两个数之后的每一个数都是前两个数的和
我们可以通过下面这个方程来描述斐波纳契数列

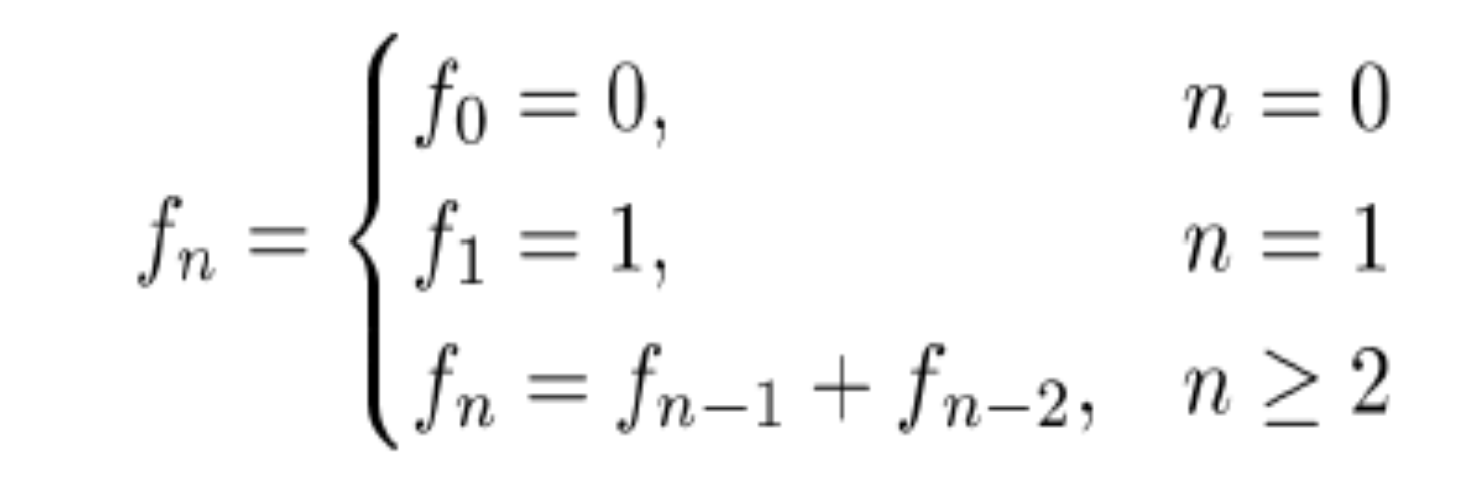
从迭代的角度来看斐波那契数列：
为了计算任何斐波那契数“n”，我们需要知道斐波那契数“n -1”和“n -2”，对于迭代版本，我们从第一个数字（n = 0）开始
随后我们计算1，2两个数字，之后是2,3，然后是3,4…以此不断推进，那么可以按照这个思想得到下面这个算法

public static int FibIter(int n){
  int prevl =0 , prev2 = 1 ; 
  int savePrev1 = 0 ;
  for(int i = 0 ; i <n ; i ++){
    savePrev1 = prev1 ; 
    prev1 = prev2 ; 
    prev2 = savePrev1 + prev2 ; 
  }
    return prev1 ; 
}

从递归的角度来看斐波那契数列：
在之前的方程中，实质上已经包含的基本情况和递归步骤

我们可以得到在递归角度的如下代码：

public static int Fib(int n){
  if(n == 0 ) {
     return 0 ;
  } 
  else if(n == 1 ) {
     return 1 ;
      //注意，这里是else if ，当第一个基本情况不满足时，才去判定第二个。当二者都不符合，再进入递归步骤
  }else{
    return Fib(n-1) + Fib(n-2) ;   //就是这一步，实质上实现了F(n) = F(n-1) + F(n-2) 的操作  
}

迭代和递归两种方法得到的答案是一样的，但是运行的过程和核心是非常不同的
采用递归的思想进行计算时，先不断堆栈达到基本情况（0或1），然后再由基本情况向目标推进

【递归：函数功能定义 Functional Definitions】
我们经常会遇到用递归函数定义的问题——就像我们在斐波那契数列中看到的那样,问题的定义通常用数学的方法(方程)写成
就像这种形式的方程，我们便可以使用递归

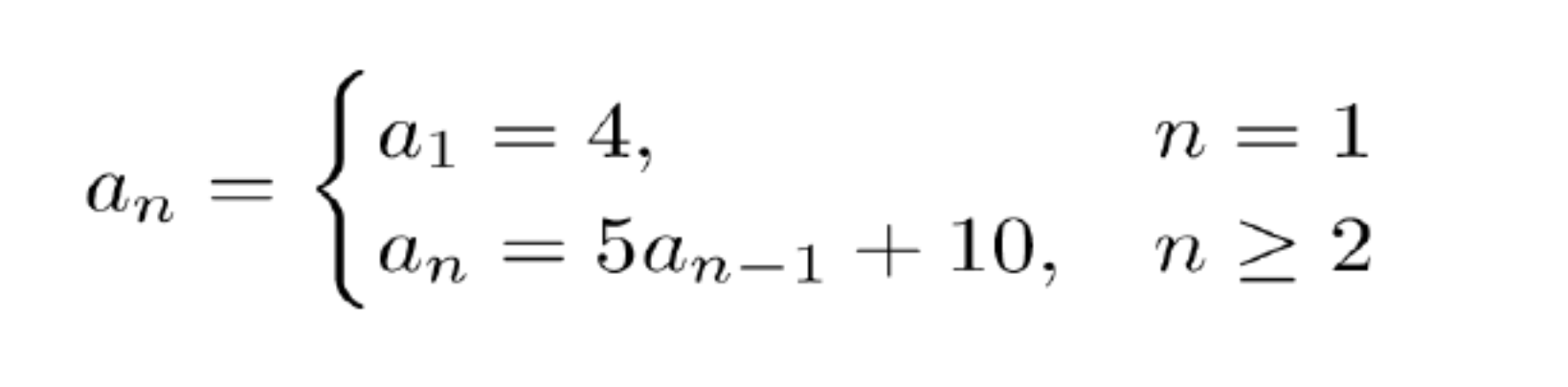
在这种情况下，递归常常会比迭代更加直观

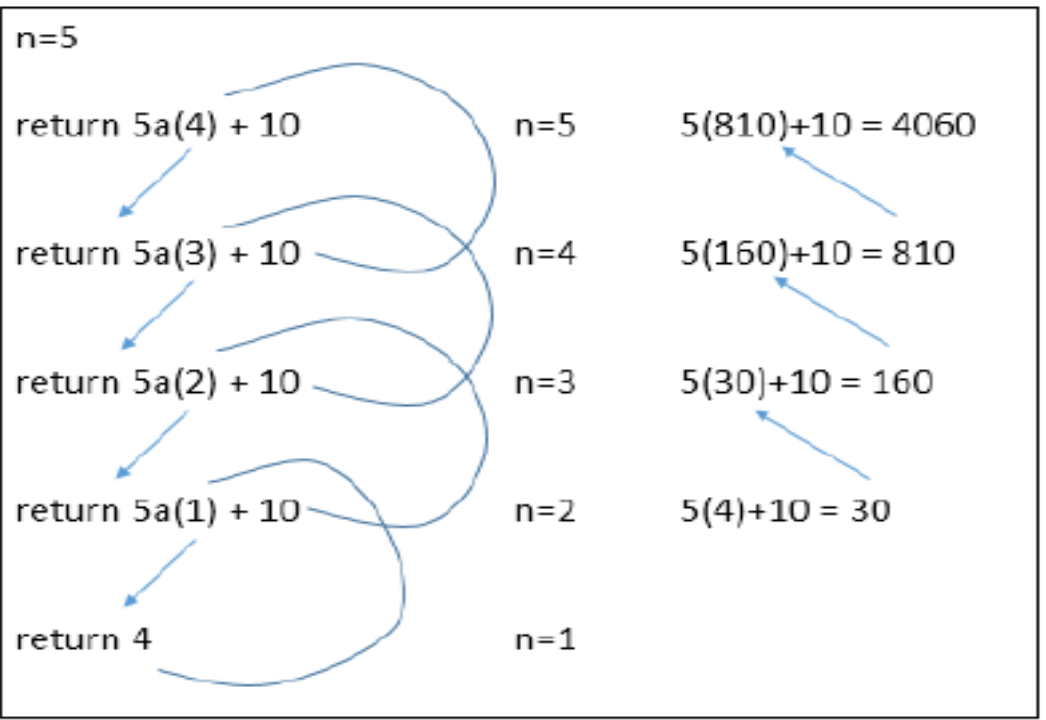
public static int FuncA(int n) {
    if(n == 1 ){
      return 4 ; 
     }else{
      return (5* Func(n-1)+10);
      }
}

【递归与数组 Recursion with Arrays】
递归还可以用于查找存储在数组中的最大值和最小值，让我们尝试一个寻找数组最大值的例子：
首先是找到基本情况，我们将假定将从当前元素开始遍历整个数组。基本情况是，当我们查看数组中的最后一个元素的时候————这时候我们已经知道了我们遍历了数组中的所有元素，所以我们从此跳出递归
那么递归步骤呢，这个其实很简单：我们将每个元素与当前存储的最大元素进行比较，如果当前正在查看的元素大于当前最大存储元素，则将该值更新为新的最大值

附：Math.max ： Math.max(int a, int b)，会返回a、b中的较大者，需要import java.lang.* ; 后使用

public static int maxArray(int [] array , int start){
    if(start == array.lengrh - 1){
          return array[start] ;  //一个基本情况：在start=数组长度时，我们就遍历了所有的数组
      }else{
          return (Math.max(array[start],maxArray(array,start + 1)));
        }
}

可能光看代码比较抽象，来看看这张示意图：

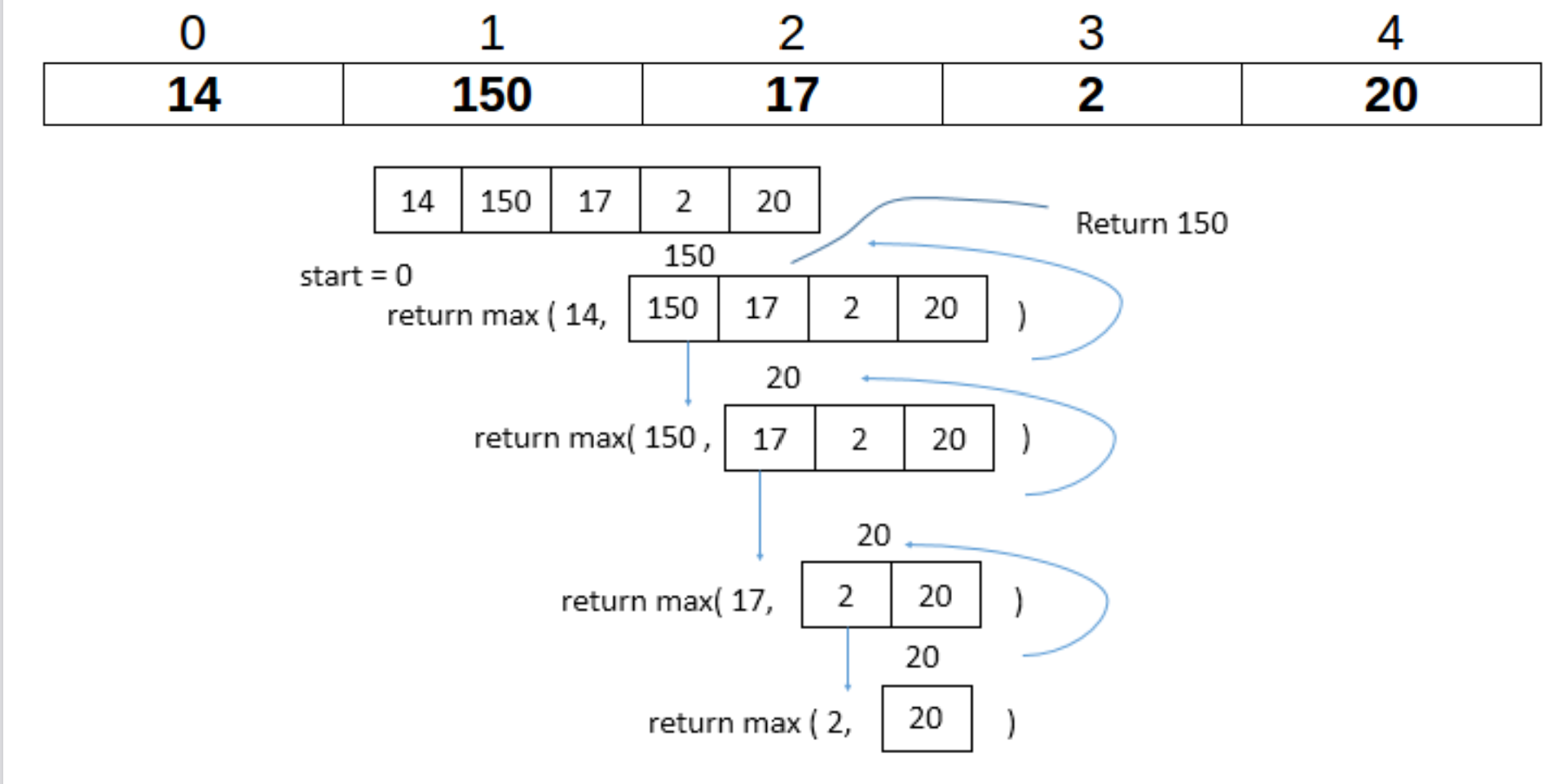
实际上，这种递归就像是一种计数器一样的递归：递归一次，做完操作我就+1。当操作计数达到了要求，就结束递归
【小结：递归的优缺点】
缺点：
•递归反复调用该方法，该方法在内存和处理时间方面会产生成本
•每次递归调用都会创建该方法的另一个副本(及其所有变量)
•这种方法的复制会消耗大量的内存空间
优点：
•如果我们对原始问题做一些细微的改变，就会更容易找到递归的解决方案
•有时，递归解决方案的运行速度会比迭代解决方案慢，不过，在大多数情况下，它只是稍微慢一些
•在许多情况下，递归解决方案比迭代解决方案更容易理解和编写代码