本文探讨了表示空间(R)和抽象空间(A)的概念，以及它们之间的映射关系。表示空间包含实际实体值，而抽象空间涉及抽象类型的值。映射是一个满射，但不是单射或双射。抽象函数描述了从表示到抽象的转换。表示不变量用于验证表示值是否符合特定条件。这些概念在理解计算机科学中的类型系统和数据表示方面至关重要。
我们先来介绍两种类型空间的值：
一、 Space of representation values （表示空间） R
表示空间由事实上实现的实体值构成。换句话说，由不同的、对抽象类型的实现的对象相应表示（Representation）的值组成。
二、 Space of abstract values (抽象空间） A
抽象空间由抽象类型设计支持的类型组成。直观来说，就是抽象类型中设计的域或者说是支持变量。它们不是实际存在的实体，但是我们透过它们来理解抽象类型的元素。
一个例子：
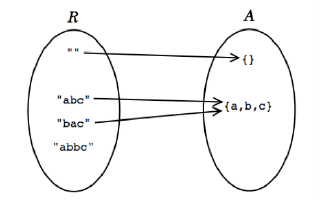
我们在这个例子里我们使用字符串来表示字母的集合。
R和A之间的映射：
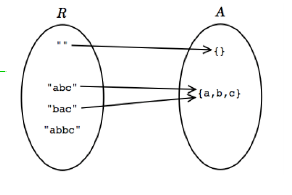
1. 每一个抽象空间的值都被映射到，是一个满射（surjective）
2. 一些抽象类型的值被不止一个表示变量值映射，所以不是一个单射（not injective）
3. 不是所有表示变量值都在映射当中，不是一个双射（not bijective）
抽象函数（Abstract Function）
抽象函数是表示从表示空间到抽象空间映射的函数
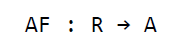
表示不变量（Rep Invariant）
表示不变量将表示变量值映射成一个布尔值。
可以将RI理解成一个表示值的子集，如果一个RI的值在到AF的映射当中，那么这个RI也就在这个子集当中，相应地，布尔值为真。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
