【BIT矩阵分析】第5章 范数 幂级数

文章汇总可见上面的专栏 或者 共享文档链接，可在下面的在线文档 或者 本文里评论指错，谢谢大家的共同努力：BIT研究生矩阵分析速成指南

文章有目录，标题里有⭐❗的重点看看，一定要懂哈！

本专栏内容基本涵盖考点，适用于 北京理工大学 研究生 矩阵分析课程，标⭐❗的看会基本能做计算题，足够及格，证明题主要分布在第3章和第5章。

第五章 矩阵范数 向量范数 幂级数，必考矩阵范数填空题，算列和范数、行和范数、F-范数、谱范数。大题大概率考证明。大题几乎必考幂级数收敛证明+求收敛和。

⭐考点速览

除了这些，一定要看看后面的证明题！！！

填空题

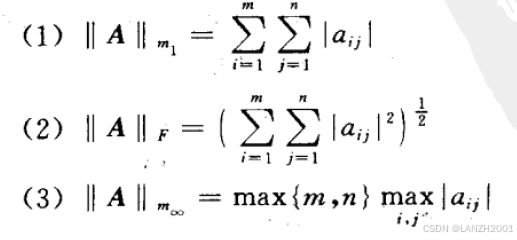
重点：Frobenius/F-范数

即：每个元素的平方和后开平方

注意谱范数求的是AHA的λ，还要开根号

可以看作是最大的奇异值。

注意列和/行和范数求和的是模（没有复数那就是绝对值）

 

证明题

证明是矩阵范数

记住四个定义条件，只需要证明这四个条件即可：非负，齐次，三角不等，乘法相容

（如果证明向量范数，不需要证乘法相容，只需证 非负，齐次，三角不等）

证明收敛

必考：证明收敛+求收敛和。

证明收敛很简单，求收敛半径，对比矩阵的最大特征值。

求收敛和比较麻烦，记公式吧。

向量范数

⭐定义条件

证明题会用到

非负+齐次+三角不等

p-范数计算

 

矩阵范数

⭐定义条件

证明题会用到

非负+齐次+三角不等+相容性

⭐Frobenious范数 _F

所有元素平方之和的开方

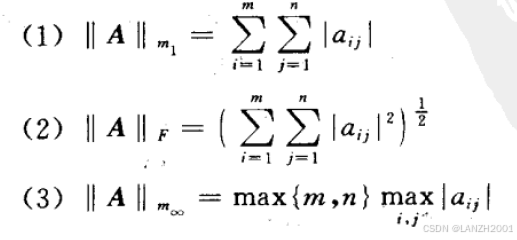
重点：Frobenius/F-范数

即：每个元素的平方和后开平方

诱导范数

⭐列和范数 谱范数 行和范数

1. 列和范数：列元素的绝对值之和的最大值

2. 谱范数：AHA的最大的特征值的开方

3. 行和范数：行元素的绝对值之和的最大值

注意谱范数求的是AHA的λ，还要开根号

可以看作是最大的奇异值

注意列和/行和范数求和的是模（如果是实数，那就是绝对值）

⭐例题

⭐矩阵范数证明题

只需证明四个条件：

⭐❗矩阵幂级数收敛证明题

⭐向量范数证明题

2024年下半年考到了5-6

感谢：

Bilibili（必看）：翟男不宅的个人空间-翟男不宅个人主页-哔哩哔哩视频

Bilibili（校友总结）：学疯蔚然的个人空间-学疯蔚然个人主页-哔哩哔哩视频

Bilibili（校友总结）：这是谁啊好难猜的个人空间-这是谁啊好难猜个人主页-哔哩哔哩视频

Github（必看）：GitHub - DarkIceField/BIT_Matrix_Analysis

Bilibili：翰林苑长的个人空间-翰林苑长个人主页-哔哩哔哩视频

Bilibili：热爱读研的铛铛的个人空间-热爱读研的铛铛个人主页-哔哩哔哩视频

如有侵权，请联系删除