《Python深度学习》读书笔记（一）

1.1 人工智能、机器学习与深度学习

对于一个如下的分类的问题，我们使用一个非常简单的线性函数就可以将这两个类别分开：

但如果是对于如下一个分类问题，我们无法使用线性分类器就将这个划分开来，但是我们可以使用两层的线性分类就可以将其分开，具体怎么做呢：

具体做法如下：比如我们都学习过AND逻辑，我们通过写出它的逻辑表以及图形，可以看出AND逻辑它可以被线性分类：

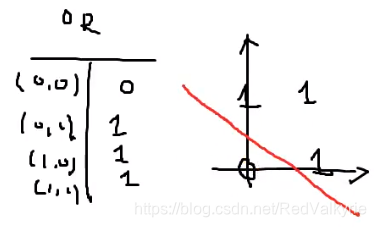
同时我们也学习过OR逻辑，同样写出它的逻辑关系与图形，我们一样可以用一个直线将其进行分类：

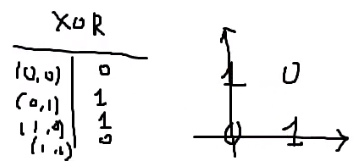
假如现在有一个XOR的逻辑，两数相同得0，两数不同得1，我们将它表示在坐标平面上，此时它是无法通过一条直线就将其线性分类的：

在这里我们想要知道的是通过神经网络，我们可以通过两层的线性分类器就将一个非线性的东西分开，具体做法如下：

1. 先构建一个NOTAND逻辑和一个OR逻辑
2. 对两个逻辑的结果取AND逻辑
   
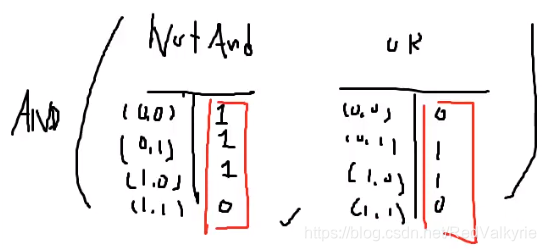
   最终得到的逻辑如下：
   
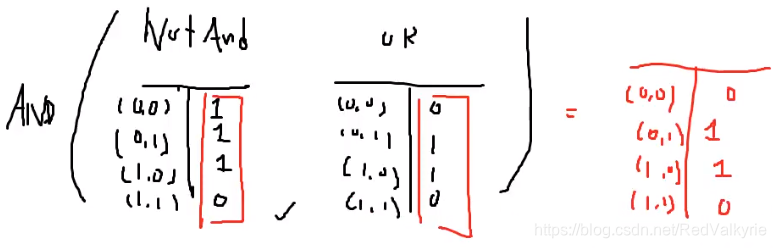
   此时我们发现它得到的结果就是XOR逻辑，结果表示我们可以通过很多层的线性分类结果得到一个可以对不好线性分类的问题做非线性分割。这也是我们为什么在深度学习每一层的最后要通过非线性激活函数，因为经过非线性转换后，就可能将一个本来不可线性分类的问题进行分类。

所以引出深度学习的一个技术性定义：学习数据表示的多级方法

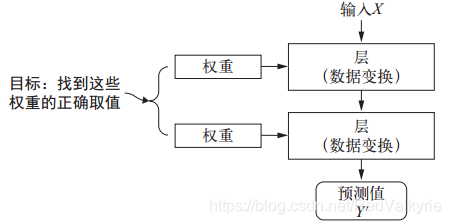
下面通过三张图对深度学习概念进行描述：

• 神经网络是由其权重来参数化
  
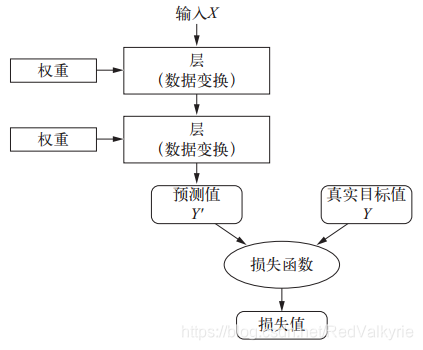
• 损失函数用来衡量网络输出结果的质量
  
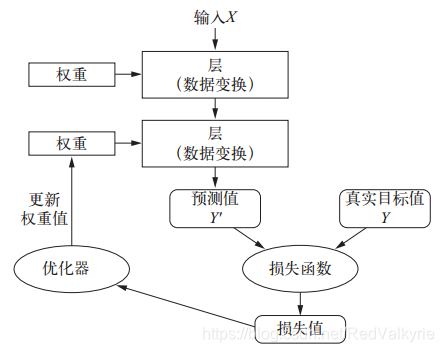
• 将损失值作为反馈信号来调节权重
  

1.2 机器学习简史

1.2.1 概率建模

• Q1：朴素贝叶斯为什么是个分类器？
• Q2：朴素贝叶斯假设输入数据的特征都是独立的，这个假设用在什么地方？

解释：
此时，假设给定类别C1（发信用卡），和C2（不发信用卡）的两个类别里，受收入和年龄两个变量约束的情况下，抽样人的分布如下：

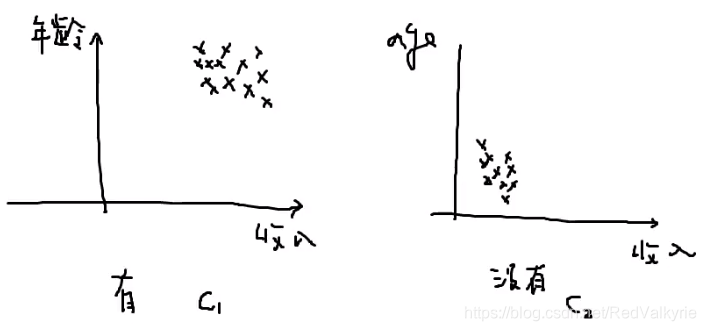
此时的x受两个特征约束，所以x是一个二维向量：

假如现在进行抽样，请问这个人被发信用卡的概率，公式如下：

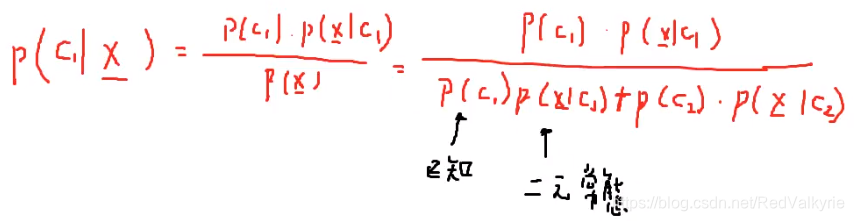
其中的 $P(C1)$ 和 $P(C2)$ 是已知的，而 $P(x|C1)$ 和 $P(x|C2)$是符合某个概率分布的，需要我们自己去估计。在这种受两个特征约束的情况下，只要我们把这个概率的参数估计出来，那我们就能算出这个概率 $P(C1|x)$，现在输入一个x，就能预估他被发信用卡的概率。

以上问题仅仅只有两个解释变束，相对还是能算出来的，现在随着解释变束的增多，你需要估计的参数是越来越多的。比如现在有三个解释变束的情况下公式为：

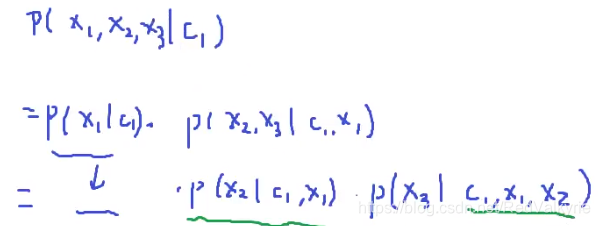
此时可以看到由贝叶斯公式展开的时候，绿色波浪线标注的概率分布需要估算的参数使很麻烦的，随着解释变束的增多这个过程也会越来越复杂，所以为了简化，需要引入朴素贝叶斯的假设，就是各个解释变束之间是相互独立的。此时在给定 $x1$ 的条件下去求 $x2$ 发生的概率和不给定 $x1$ 时，单独给定 $C1$ 去求 $x2$ 的概率是相同的。所以以上公式可以进行替换，结果如下：

此时，我们只是用一元常态就能估计这个问题。问题就得到了简化，这时候就算是解释变束有100个我们通过假设每个解释变束之间是独立的就可以解决掉这个分类问题。早期的机器学习也就是通过类似这些概率的方法来进行建模的。

1.2.3 核方法

• Q：为什么SVM要将数据映射到一个新的高维表示

比如对于如下训练数据的分布，我们其实是无法对其线性可分的：

但是我们可以对原始的数据进行一些非线性的转换，对于这里我们可以把这张图想象成一张纸，然后沿着 $x1$ 这条轴对折一下，然后再沿着 $x2$ 这条轴对折，最后得到如下的结果：

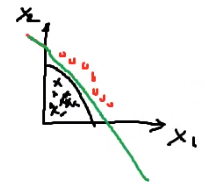
此时我们发现它就可以被一条线性函数分开。这个过程就是将数据映射到一个更高维的平面，比如现在它最开始是一个平面，现在被对折几次经过变换就到了一个更高的维度。

这是本人第一篇博客，欢迎大家一起学习交流，谢谢点赞转发，同时安利一个自己的微信公众号，一起加油：