算法的时间复杂度
度量一个程序(算法)执行时间的两种方法:
- 事后统计的方法:这种方法可行, 但是有两个问题:
- 一是要想对设计的算法的运行性能进行评测,需要实际运行该程序;
- 二是所得时间的统计量依赖于计算机的硬件、软件等环境因素, 这种方式,要在同一台计算机的相同状态下运行,才能比较那个算法速度更快。
- 事前估算的方法:通过分析某个算法的时间复杂度来判断哪个算法更优.
时间频度T(n)T(n)T(n)
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)T(n)T(n)。
例子:计算1-100所有数字之和
时间频度:T(n)=n+1T(n)=n+1T(n)=n+1
int total = 0;
int end = 100;
//使用for循环计算
for(int i=1;i<=end;i++){
total=+i;
}
时间频度:T(n)=1T(n)=1T(n)=1
total = (1+end)*end/2;
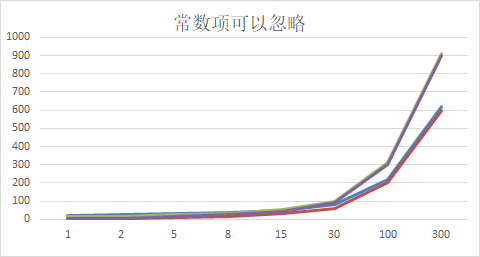
忽略常数项
- 2n+20 和 2n 随着n 变大,执行曲线无限接近, 20可以忽略
- 3n+10 和 3n 随着n 变大,执行曲线无限接近, 10可以忽略
| T(n)=2n+20T(n)=2n+20T(n)=2n+20 | T(n)=2∗nT(n)=2*nT(n)=2∗n | T(3n+10)T(3n+10)T(3n+10) | T(3n)T(3n)T(3n) | |
|---|---|---|---|---|
| 1 | 22 | 2 | 13 | 3 |
| 2 | 24 | 4 | 16 | 6 |
| 5 | 30 | 10 | 25 | 15 |
| 8 | 36 | 16 | 34 | 24 |
| 15 | 50 | 30 | 55 | 45 |
| 30 | 80 | 60 | 100 | 90 |
| 100 | 220 | 200 | 310 | 300 |
| 300 | 620 | 600 | 910 | 900 |
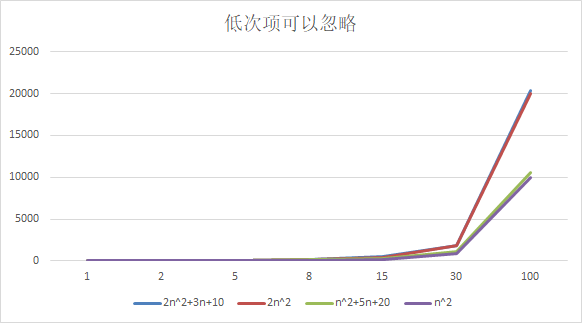
忽略低次项
- 2n2+3n+102n^2+3n+102n2+3n+10 和 2n22n^22n2 随着n 变大, 执行曲线无限接近, 可以忽略 3n+10
- n2+5n+20n^2+5n+20n2+5n+20 和 n2n^2n2 随着n 变大,执行曲线无限接近, 可以忽略 5n+20
| T(n)=2n2+3n+10T(n)=2n^2+3n+10T(n)=2n2+3n+10 | T(2n2)T(2n^2)T(2n2) | T(n2+5n+20)T(n^2+5n+20)T(n2+5n+20) | T(n2)T(n^2)T(n2) | |
|---|---|---|---|---|
| 1 | 15 | 2 | 26 | 1 |
| 2 | 24 | 8 | 34 | 4 |
| 5 | 75 | 50 | 70 | 25 |
| 8 | 162 | 128 | 124 | 64 |
| 15 | 505 | 450 | 320 | 225 |
| 30 | 1900 | 1800 | 1070 | 900 |
| 100 | 20310 | 20000 | 10520 | 10000 |
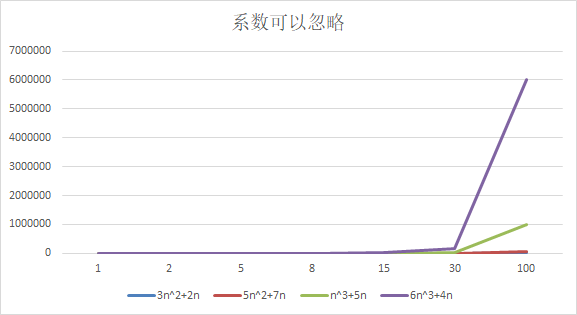
忽略系数
- 随着n值变大,5n2+7n5n^2+7n5n2+7n 和 3n2+2n3n^2 + 2n3n2+2n ,执行曲线重合, 说明 这种情况下, 5和3可以忽略。
- 而n3+5nn^3+5nn3+5n 和 6n3+4n6n^3+4n6n3+4n ,执行曲线分离,说明多少次方式关键
| T(3n2+2n)T(3n^2+2n)T(3n2+2n) | T(5n2+7n)T(5n^2+7n)T(5n2+7n) | T(n3+5n)T(n^3+5n)T(n3+5n) | T(6n3+4n)T(6n^3+4n)T(6n3+4n) | |
|---|---|---|---|---|
| 1 | 5 | 12 | 6 | 10 |
| 2 | 16 | 34 | 18 | 56 |
| 5 | 85 | 160 | 150 | 770 |
| 8 | 208 | 376 | 552 | 3104 |
| 15 | 705 | 1230 | 3450 | 20310 |
| 30 | 2760 | 4710 | 27150 | 162120 |
| 100 | 30200 | 50700 | 1000500 | 6000400 |
时间复杂度O(f(n))O(f(n))O(f(n))
一般情况下,算法中的基本操作语句的重复执行次数是问题规模n的某个函数,用时间频度T(n)T(n)T(n)表示;若有某个辅助函数f(nf(nf(n),使得当n趋近于无穷大时,limn→∞T(n)f(n)\lim_{n\to \infty}\frac{T(n)}{f(n)}limn→∞f(n)T(n) 的极限值为不等于零的常数,则称f(n)f(n)f(n)是T(n)T(n)T(n)的同数量级函数。记作 $T(n)=O(f(n)) ,称,称,称O(f(n))$ 为算法的渐进时间复杂度,简称时间复杂度。
T(n)T(n)T(n) 不同,但时间复杂度可能相同。 如:T(n)=n²+7n+6T(n)=n²+7n+6T(n)=n²+7n+6 与 T(n)=3n²+2n+2T(n)=3n²+2n+2T(n)=3n²+2n+2 它们的T(n)T(n)T(n) 不同,但时间复杂度相同,都为O(n²)O(n²)O(n²)。
计算时间复杂度的方法
- 用常数1代替运行时间中的所有加法常数 T(n)=n2+7n+6T(n)=n^2+7n+6T(n)=n2+7n+6 => T(n)=n2+7n+1T(n)=n^2+7n+1T(n)=n2+7n+1
- 修改后的运行次数函数中,只保留最高阶项 T(n)=n2+7n+1T(n)=n^2+7n+1T(n)=n2+7n+1 => T(n)=n2T(n) = n^2T(n)=n2
- 去除最高阶项的系数 T(n)=n2T(n) = n^2T(n)=n2 => T(n)=n²T(n) = n²T(n)=n² => O(n²)O(n²)O(n²)
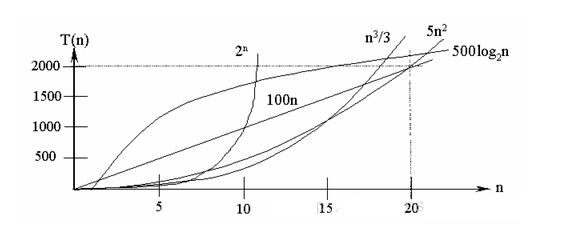
常见的时间复杂度
常见的算法时间复杂度由小到大依次为:O(1)Ο(1)O(1)<O(log2n)Ο(log_2^n)O(log2n)<Ο(n)<O(nlog2n)Ο(nlog_2^n)O(nlog2n)<O(n2)Ο(n^2)O(n2)<O(n3)Ο(n^3)O(n3)< O(nk)Ο(n^k)O(nk) <O(2n)Ο(2^n)O(2n) ,随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低
- 常数阶O(1)O(1)O(1)
- 对数阶O(log2n)O(log_2^n)O(log2n)
- 线性阶O(n)O(n)O(n)
- 线性对数阶O(nlog2n)O(nlog_2^n)O(nlog2n)
- 平方阶O(n2)O(n^2)O(n2)
- 立方阶O(n3)O(n^3)O(n3)
- k次方阶O(nk)O(n^k)O(nk)
- 指数阶O(2n)O(2^n)O(2n)
从图中可见,我们应该尽可能避免使用指数阶的算法
常数阶O(1)O(1)O(1)
无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1)O(1)O(1)
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
上述代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)O(1)O(1)来表示它的时间复杂度。
对数阶O(log2n)O(log_2^n)O(log2n)
对数阶:以2为底nnn的对数,有些书上记做O(logN)O(logN)O(logN)或者O(lgN)O(lgN)O(lgN)
- 一般地,在国内lglglg默认以10为底。
- 如果 N=ax(a>0,a≠1)N=a^x(a>0,a\ne1)N=ax(a>0,a=1) ,即aaa的x次方等于N(a>0,且a≠1)N(a>0,且a≠1)N(a>0,且a=1),那么数xxx叫做以aaa为底NNN的对数(logarithm),记作x=logaNx=log_a^Nx=logaN。其中,a叫做对数的底数,N叫做真数,x叫做以a为底N的对数。
int i = 1;
while(i < n){
i = i * 2;
}
- 在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,即 x=log2nx=log_2^nx=log2n.
- 也就是说当循环 log2nlog_2^nlog2n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(log2n)O(log_2^n)O(log2n) 。O(log2n)O(log_2^n)O(log2n) 的这个2 时间上是根据代码变化的,i = i * 3 ,则是 O(log3n)O(log_3^n)O(log3n)
线性阶O(n)O(n)O(n)
for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)O(n)O(n)来表示它的时间复杂度。
for(i = 1;i <= n; ++i){
j=i;
j++;
}
线性对数阶O(nlog2n)O(nlog_2^n)O(nlog2n)
线性对数阶O(nlog2n)O(nlog_2^n)O(nlog2n)其实非常容易理解,将时间复杂度为O(log2n)O(log_2^n)O(log2n)的代码循环N遍的话,那么它的时间复杂度就是 nO(logN)n O(logN)nO(logN),也就是了O(nlog2n)O(nlog_2^n)O(nlog2n)
for(m=1;m<n;m++){
int i = 1;
while(i < n){
i = i * 2;
}
}
平方阶O(n2)O(n^2)O(n2)
平方阶O(n2)O(n^2)O(n2) 就更容易理解了,如果把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n2)O(n^2)O(n2),这段代码其实就是嵌套了2层n循环,它的时间复杂度就是 O(n×n)O(n\times n)O(n×n),即 O(n2)O(n^2)O(n2) 如果将其中一层循环的n改成m,那它的时间复杂度就变成了 O(n×m)O(n\times m)O(n×m)
for(x = 1;i <= n; x++){
for(i = 1;i <= n; ++i){
j=i;
j++;
}
}
立方阶O(n3)O(n^3)O(n3)
参考上面的O(n2)O(n^2)O(n2)去理解,O(n3)O(n^3)O(n3)相当于三层nnn循环
k次方阶O(nk)O(n^k)O(nk)
参考上面的O(n2)O(n^2)O(n2)去理解,O(nk)O(n^k)O(nk)相当于kkk层nnn循环
指数阶O(2n)O(2^n)O(2n)
平均时间复杂度和最坏时间复杂度
- 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下,该算法的运行时间。
- 最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。 这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限,这就保证了算法的运行时间不会比最坏情况更长。
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡 | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | 稳定 | O(1)O(1)O(1) | n小时较好 |
| 交换 | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | 不稳定 | O(1)O(1)O(1) | n小时较好 |
| 选择 | O(n^3) | O(n2)O(n^2)O(n2) | 不稳定 | O(1)O(1)O(1) | n小时较好 |
| 插入 | O(n2)O(n^2)O(n2) | O(n2)O(n^2)O(n2) | 稳定 | O(1)O(1)O(1) | 大部分己排序时较妇 |
| 基数 | O(logRB)O(log_R^B)O(logRB) | O(logRB)O(log_R^B)O(logRB) | 稳定 | O(n)O(n)O(n) | B是真数(0-9) R是基数(个十百) |
| Shell | O(nlogn)O(nlogn)O(nlogn) | O(ns)O(n^s)O(ns) 1<s<2 | 不稳定 | O(1)O(1)O(1) | s是所选分组 |
| 快速 | O(nlogn)O(nlogn)O(nlogn) | O(n2)O(n^2)O(n2) | 不稳定 | O(nlogn)O(nlogn)O(nlogn) | n大时较好 |
| 归并 | O(nlogn)O(nlogn)O(nlogn) | O(nlogn)O(nlogn)O(nlogn) | 稳定 | O(1)O(1)O(1) | n大时较好 |
| 堆 | O(nlogn)O(nlogn)O(nlogn) | O(nlogn)O(nlogn)O(nlogn) | 不稳定 | O(1)O(1)O(1) | n大时较好 |





 本文深入探讨了算法的时间复杂度,包括事后统计和事前估算方法,解释了时间频度的概念,展示了如何通过忽略常数项、低次项和系数来简化时间复杂度的表达,并列举了常见的复杂度类型及其效率对比。
本文深入探讨了算法的时间复杂度,包括事后统计和事前估算方法,解释了时间频度的概念,展示了如何通过忽略常数项、低次项和系数来简化时间复杂度的表达,并列举了常见的复杂度类型及其效率对比。
















 1014
1014

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








