字串差值 dp

最新推荐文章于 2025-12-11 20:57:05 发布

原创最新推荐文章于 2025-12-11 20:57:05 发布 · 145 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #图论

码题集同时被 2 个专栏收录

12 篇文章

订阅专栏

4 篇文章

订阅专栏

该博客介绍了一种使用动态规划求解字符串编辑距离的方法。通过输入两个字符串和一个步长，代码计算出将一个字符串转换为另一个所需的最少操作数。思路是每一步都选取最小操作，递推填充dp矩阵，最终得到最小编辑距离。

题面：
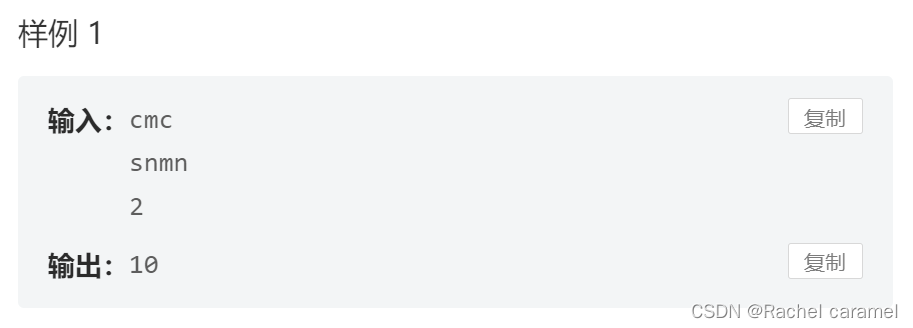
在这里插入图片描述

输入：
cmc
snmn
2

思路：
每一步都取最小值，最后的值一定是最小的
利用dp递推
代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn=2111;
char a[maxn],b[maxn];
int k,n,m,f[maxn][maxn];
int main() 
{
	cin>>(a+1)>>(b+1)>>k;
	n=strlen(a+1),m=strlen(b+1);
	for(int i=1;i<=n;i++) f[i][0]=i*k;
	for(int i=1;i<=m;i++) f[0][i]=i*k;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++) 
		{
			f[i][j]=min(min(f[i-1][j],f[i][j-1])+k,f[i-1][j-1]+abs(a[i]-b[j]));
			//cout<<"i="<<i<<" "<<"j="<<j<<" "<<"f[i][j]="<<f[i][j]<<endl;
		}
	}
	cout<<f[n][m]<<endl;
	return 0;
}