11. Container With Most Water

最新推荐文章于 2022-07-23 19:08:46 发布

原创最新推荐文章于 2022-07-23 19:08:46 发布 · 143 阅读

0 ·

CC 4.0 BY-SA版权

leetcode 专栏收录该内容

58 篇文章

订阅专栏

本文探讨了如何从一组垂直线中找出能构成最大盛水量的两条线的问题。通过对比两种算法，暴力法和优化法，详细解释了优化法如何通过从两端向中间扫描并移动较短边来提高效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.
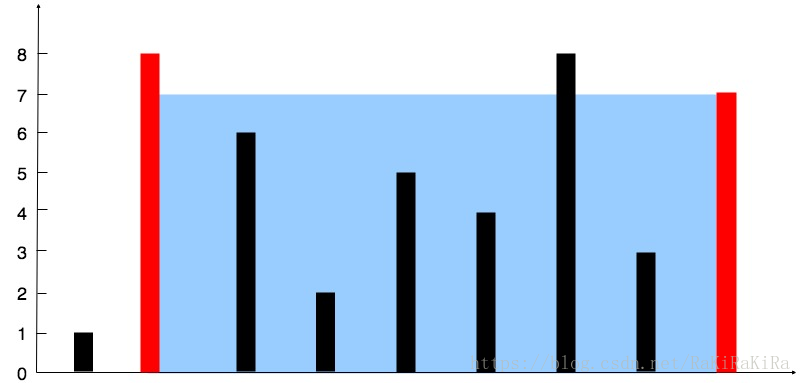
在这里插入图片描述
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example:

Input: [1,8,6,2,5,4,8,3,7]
Output: 49

简单来说就是给一堆高，问取哪两个高围的面积最大

思路1：暴力

没什么好说的直接过一遍

#define MIN(A,B) A<B?A:B
int maxArea1(vector<int>& height) {
	int sz = height.size(), res = 0, temp = 0;
	for(int i=0;i<sz;++i)
		for (int j = i + 1; j < sz; ++j) {
			temp = (j - i)*(MIN(height[i], height[j]));
			if (temp > res) res = temp;
		}
	return res;
}

思路2：优化

在上述暴力方法的基础上，寻找可以优化的地方
假设初始面积是取最左和最右两个高计算得到，从两边向中间扫描
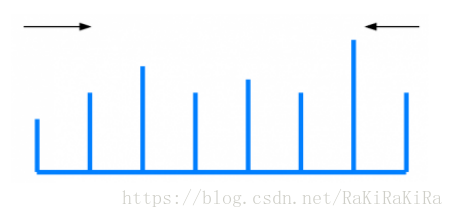
在这里插入图片描述
每次选当前两高中较短的一边向另一边移动，计算面积并与之前值比较。
这样操作时因为，边移动时会使两边距离变小，而计算面积时是根据较短边的高度计算的，移动较长边不会得到任何收益（移动到更长边还是使用另一边高，移动到更短边会使面积再次减少）。

    #define MIN(A,B) A<B?A:B
	int maxArea(vector<int>& height) {
		int j = height.size()-1, res = 0, temp = 0;
		int i = 0;
		while(i<j){
			temp = (j - i)*(MIN(height[i], height[j]));
			if (temp > res) res = temp;
			height[i] > height[j] ? --j : ++i;
		}
		return res;
	}