Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d
distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
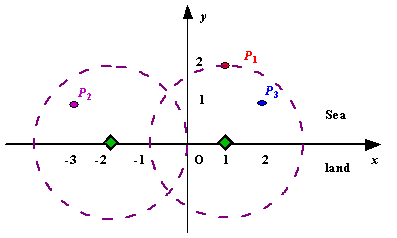
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is
followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
本来是想从海岸上找雷达,再去看能够覆盖到那几个,不知道为啥不对。后来看到别人的代码是以海岛为圆心,距离d为半径做圆,看在海岸上的区间覆盖,然后找点、
先贴上错的那个代码,就是第一种思路的
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<math.h>
struct node
{
double x, y;
} ls[1010],ll;
int main()
{
int n, d;
int kk = 0;
while(~scanf("%d%d",&n,&d))
{
kk++;
int flag = 1;
if(n == 0 && d == 0)
break;
int i, j, k;
for(i = 0; i < n; i++)
{
scanf("%lf%lf",&ls[i].x,&ls[i].y);
if(ls[i].y > d)
flag = 0;
}
if(!flag)
{
printf("Case %d: -1\n",kk);
continue;
}
for(i = 0; i < n; i++)
{
k = i;
for(j = i; j < n; j++)
{
if(ls[j].x < ls[k].x)
k = j;
}
if(k != i)
{
ll = ls[k];
ls[k] = ls[i];
ls[i] = ll;
}
}
int c = 0;
double x0;
x0 = ls[0].x + sqrt(d*d - ls[0].y*ls[0].y);
c = 1;
for(i = 1; i < n; i++)
{
if(pow(ls[i].x - x0,2) - pow(ls[i].y,2) <= pow(d,2))
{
continue;
}
else
{
x0 = ls[i].x + sqrt(d*d - ls[i].y*ls[i].y);
c++;
}
}
printf("Case %d: %d\n",kk,c);
}
return 0;
}再贴上第二种思路的代码
#include <iostream>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<cmath>
#include<cstdio>
using namespace std;
struct node
{
double x1, x2;
} ls[1010];
bool cmp(node x,node y)
{
return x.x1 < y.x1;
}
int main()
{
int n, d, k = 0;
while(~scanf("%d%d",&n,&d)&&(n+d))
{
k++;
int i;
bool flag = true;
for(i = 0; i < n; i++)
{
double x, y;
scanf("%lf %lf",&x,&y);
if(y > d)
{
flag = false;
continue;
}
ls[i].x1 = x - sqrt(pow(d,2)- pow(y,2));
ls[i].x2 = x + sqrt(pow(d,2)- pow(y,2));
}
if(!flag)
{
printf("Case %d: -1\n",k);
continue;
}
sort(ls,ls+n,cmp);
double r = ls[0].x2;
int c = 1;
for(i = 1; i < n; i++)
{
if(ls[i].x2 < r)
{
r = ls[i].x2;
}
else if(ls[i].x1 > r)
{
c++;
r = ls[i].x2;
}
}
printf("Case %d: %d\n",k,c);
}
return 0;
}







 本文探讨了在海岸线上合理布置雷达安装以覆盖海上岛屿的最优化问题,通过使用直角坐标系来定位岛屿和雷达,计算所需雷达数量以确保所有岛屿被覆盖。文章详细解释了解决该问题的方法,并提供了实例输入输出进行验证。
本文探讨了在海岸线上合理布置雷达安装以覆盖海上岛屿的最优化问题,通过使用直角坐标系来定位岛屿和雷达,计算所需雷达数量以确保所有岛屿被覆盖。文章详细解释了解决该问题的方法,并提供了实例输入输出进行验证。
















 2676
2676

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








