法1: 旋转数组的特点:
1,旋转之后的数组可以分为两个排序的子数组,且前面的子数组的元素都大于或等于后面子数组的元素。
2,最小或者最大元素位于两个子数组的分界
解题思路:在排序数组中,可以使用二分查找法进行查找
利用左右两个指针和中间指针元素大小关系判断中间元素是位于前面的子数组还是后面的子数组,缩小查找范围
需要考虑的特例:
1,排序数组本身仍是该数组的一个旋转
2,如果数组内有重复元素,那么有可能出现左右两指针元素与中间元素相同,无法判断中间元素属于前面子数组还是后面子数组,此时用顺序查找/ * 如果把排序数组前面的0个元素搬到最后面,即排序数组本身,这仍然是数组的一个旋转。
* 此时,数组中的第一个数字就是最小的数字,可以直接返回,这就是 把indexMid初始化为index1的原因
*
* 第一个指针最终将指向前面子数组的最后一个元素,而第二个指针会指向后面子数组的第一个元素。也就是他们最终会指向*两个相邻的元素,而第二个指针指向的更好是最小的元素。这就是循环结束的条件。
*/
法2:感觉这个更好
采用二分法解答这个问题,
mid = low + (high - low)/2
需要考虑三种情况:
(1)array[mid] > array[high]:
出现这种情况的array类似[3,4,5,6,0,1,2],此时最小数字一定在mid的右边。
low = mid + 1
(2)array[mid] == array[high]:
出现这种情况的array类似 [1,0,1,1,1] 或者[1,1,1,0,1],此时最小数字不好判断在mid左边
还是右边,这时只好一个一个试 ,
high = high - 1
(3)array[mid] < array[high]:
出现这种情况的array类似[2,2,3,4,5,6,6],此时最小数字一定就是array[mid]或者在mid的左
边。因为右边必然都是递增的。
high = mid
注意这里有个坑:如果待查询的范围最后只剩两个数,那么mid 一定会指向下标靠前的数字
比如 array = [4,6]
array[low] = 4 ;array[mid] = 4 ; array[high] = 6 ;
如果high = mid - 1,就会产生错误, 因此high = mid
但情形(1)中low = mid + 1就不会错误
代码:
public class Offer08 {
public int minOfRotateArrays(int [] arrays) {
if(arrays == null || arrays.length <= 0)
//throw new RuntimeException("Invalid arrays");
return 0;
int index1 = 0;
int index2 = arrays.length -1;
int indexMid = index1;
while(arrays[index1] >= arrays[index2]){
if(index2 - index1 == 1){
indexMid = index2;
break;
}
indexMid = (index1 + index2)/2;
//如果下标为index1、 index2和indexMin指向的三个数字相等,则只能顺序查找
if(arrays[index1] == arrays[index2] && arrays[index1] == arrays[indexMid])
return minInOrder(arrays, index1, index2);
//旋转数组部分有序,可以使用二分查找
if(arrays[indexMid] >= arrays[index1])
index1 = indexMid;
else if(arrays[indexMid] <= arrays[index2])
index2 = indexMid;
}
return arrays[indexMid];
}
public int minInOrder(int [] arrays, int index1, int index2){//顺序查找
int result = arrays[index1];
for(int i = index1+1; i<=index2;i++){
if(result > arrays[i])
result = arrays[i];
}
return result;
}
//method 2
public int minNumberInRotateArray(int [] array) {
if(array == null || array.length==0)
return 0;
int left = 0;
int right = array.length-1;
while(left<right){
int mid = left+(right-left)/2;
if(array[mid]>array[right]){
left = mid+1;
}else if(array[mid] == array[right]){
right = right -1;
}else{
right = mid;
}
}
return array[left];
}
public static void main(String[] args) {
Offer08 of8 = new Offer08();
//测试用例
//1,功能测试(输入的数组是升序排序数组的一个旋转,数组中有重复的数组或者没有重复的数字)
int [] array1 = {3,4,5,1,2};
System.out.println("升序排序数组的一个旋转数组,无重复数字:"+ of8.minOfRotateArrays(array1));
int [] array2 = {3,4,5,1,1,2};
int [] array3 = {1,0,1,1,1};//这个例子一般想不到,特别重要,这种情况二分法没用,只能用顺序查找
int [] array4 = {1,1,1,0,1};//这个例子一般想不到,特别重要,这种情况二分法没用,只能用顺序查找
System.out.println("升序排序数组的一个旋转数组,有重复数字:"+ of8.minOfRotateArrays(array2));
System.out.println("升序排序数组的一个旋转数组,有重复数字:"+ of8.minOfRotateArrays(array3));
System.out.println("升序排序数组的一个旋转数组,有重复数字:"+ of8.minOfRotateArrays(array4));
//2,边界值测试,(输入的数组是一个升序排序的数组、只包含一个数字的数组)
int [] array5 = {1,2,3,4,5};
System.out.println("输入数组是一个升序排序数组:"+ of8.minOfRotateArrays(array5));
int [] array6 = {1};
System.out.println("输入数组是只包含一个数字的数组:"+ of8.minOfRotateArrays(array6));
//3,特殊输入测试(输入NULL指针)
int [] array7 = null;
System.out.println("输入NULL指针:"+ of8.minOfRotateArrays(array7));
}
}
运行结果:
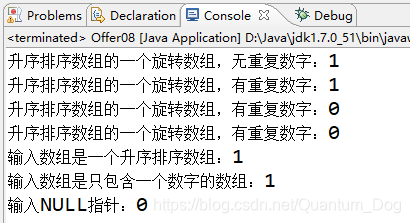





 本文介绍了一种在旋转排序数组中查找最小值的高效算法,通过二分查找法结合特殊情况处理,实现快速定位最小元素。文章详细解释了两种方法的实现细节,并提供了代码示例,同时测试了各种边界条件。
本文介绍了一种在旋转排序数组中查找最小值的高效算法,通过二分查找法结合特殊情况处理,实现快速定位最小元素。文章详细解释了两种方法的实现细节,并提供了代码示例,同时测试了各种边界条件。
















 4491
4491

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








