#include "queue.h"
BTNode* BuyBTNode(BTDataType x)
{
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->_data = x;
root->_left = NULL;
root->_right = NULL;
return root;
}
// 创建二叉树
BTNode* CreateBTree(BTDataType* a, size_t* pIndex, BTDataType invalid)
{
BTNode* root = NULL;
while (a[*pIndex] != invalid)//invalid是'#'
{
root = BuyBTNode(a[*pIndex]);
(*pIndex)++;
root->_left = CreateBTree(a, pIndex, invalid);
(*pIndex)++;
root->_right = CreateBTree(a, pIndex, invalid);
}
return root;
}
void BTreePrevOrder(BTNode* root)
{
if (root == NULL)
return;
printf("%d ", root->_data);
BTreePrevOrder(root->_left);
BTreePrevOrder(root->_right);
}
void BTreeInOrder(BTNode* root)
{
if (root == NULL)
return;
BTreeInOrder(root->_left);
printf("%d ", root->_data);
BTreeInOrder(root->_right);
}
void BTreePostOrder(BTNode* root)
{
if (root == NULL)
return;
BTreePostOrder(root->_left);
BTreePostOrder(root->_right);
printf("%d ", root->_data);
}
//结点大小
size_t BTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return BTreeSize(root->_left) + BTreeSize(root->_right) + 1;
}
//叶子数(叶子指一个结点既无左结点也无右结点)
size_t BTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->_left == NULL&&root->_right == NULL)
return 1;
return BTreeLeafSize(root->_left) + BTreeLeafSize(root->_right);
}
//第k层结点数
size_t BTreeKLevelSize(BTNode* root, size_t k)
{
if (root == NULL)
return 0;
//已经分置到第k层
if (k == 1)
{
return 1;
}
return BTreeKLevelSize(root->_left, k - 1) + BTreeKLevelSize(root->_right,k-1);
}
//最大深度
size_t BTreeDepth(BTNode* root)
{
size_t LeftDepth;
size_t RightDepth;
if (root == NULL)
return 0;
LeftDepth = BTreeDepth(root->_left);
RightDepth = BTreeDepth(root->_right);
if (LeftDepth > RightDepth)
return LeftDepth+1;
else
return RightDepth+1;
}
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
BTNode* Left;
BTNode* Right;
if (root == NULL)
return NULL;
//本节点找到了
if (root->_data == x)
return root;
//接收左节点的查找结果
Left = BTreeFind(root->_left, x);
if (Left != NULL)
return Left;
//接收右节点的查找结果
Right = BTreeFind(root->_right, x);
if (Right != NULL)
return Left;
//子节点和父结点都没有返回空
return NULL;
}
//利用队列先进后出的性质来层序遍历二叉树
//层序遍历
void BTreeLevelOrder(BTNode* root)
{
Queue queue;
BTNode* front;
//先初始化
QueueInit(&queue);
QueuePush(&queue,root);
while (QueueSize(&queue) > 0)
{
front = QueueFront(&queue);
printf("%d ", front->_data);
if (front->_left != NULL)
{
QueuePush(&queue, front->_left);
}
if (front->_right != NULL)
{
QueuePush(&queue, front->_right);
}
QueuePop(&queue);
}
}
// 判断完全二叉树
//类比层序遍历的方法
//如果同一层从左边开始查找,遇到了为空的点,那么此点后面如果全部为空说明该为完全二叉树,反之不是
int IsCompleteBTree(BTNode* root)
{
int flag = 0;
Queue queue;
BTNode* front;
//先初始化
QueueInit(&queue);
QueuePush(&queue, root);
while (QueueSize(&queue) > 0)
{
front = QueueFront(&queue);
if (front->_left != NULL)
{
QueuePush(&queue, front->_left);
}
else // 在前面遇到空就停下来
{
flag=1;
}
if (front->_right != NULL)
{
QueuePush(&queue, front->_right);
}
else//在前面遇到空就停下来
{
flag=1;
}
QueuePop(&queue);
if (flag == 1)
{
break;
}
}
QueuePop(&queue);
//停下来后判断同一层
while (QueueSize(&queue) > 0)
{
front = QueueFront(&queue);
if (front->_left != NULL)
return 0;
if (front->_left != NULL)
return 0;
QueuePop(&queue);
}
return 1;
}







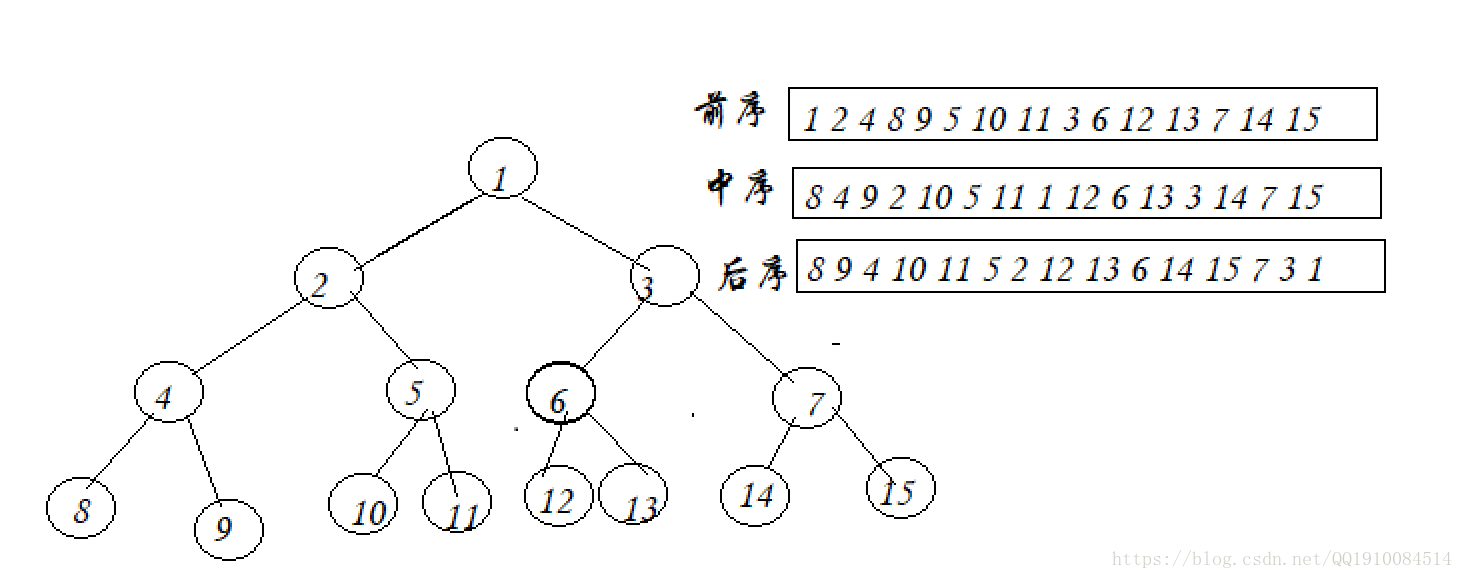
 本文详细介绍了二叉树的各种操作实现方法,包括创建、遍历(先序、中序、后序)、计算结点数量、叶子结点数量、第k层结点数、最大深度等,并提供了基于队列的层序遍历及判断是否为完全二叉树的代码示例。
本文详细介绍了二叉树的各种操作实现方法,包括创建、遍历(先序、中序、后序)、计算结点数量、叶子结点数量、第k层结点数、最大深度等,并提供了基于队列的层序遍历及判断是否为完全二叉树的代码示例。
















 489
489

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








