【蓝桥杯C++】负载均衡

有 n 台计算机，第 i 台计算机的运算能力为 vi。

有一系列的任务被指派到各个计算机上，第 i 个任务在 ai 时刻分配，指定计算机编号为 bi，耗时为 ci 且算力消耗为 di。

如果此任务成功分配，将立刻开始运行，期间持续占用 bi 号计算机 di 的算力，持续 ci 秒。

对于每次任务分配，如果计算机剩余的运算能力不足则输出 −1，并取消这次分配，否则输出分配完这个任务后这台计算机的剩余运算能力。

输入格式
输入的第一行包含两个整数 n,m，分别表示计算机数目和要分配的任务数。

第二行包含 n 个整数 v1,v2,⋅⋅⋅vn，分别表示每个计算机的运算能力。

接下来 m 行每行 4 个整数 ai,bi,ci,di，意义如上所述。数据保证 ai 严格递增，即 ai<ai+1。

输出格式
输出 m 行，每行包含一个数，对应每次任务分配的结果。

数据范围
对于 20% 的评测用例，n,m≤200。
对于 40% 的评测用例，n,m≤2000。
对于所有评测用例，1≤n,m≤200000，1≤ai,ci,di,vi≤109，1≤bi≤n。

输入样例：

2 6
5 5
1 1 5 3
2 2 2 6
3 1 2 3
4 1 6 1
5 1 3 3
6 1 3 4

输出样例：

2
-1
-1
1
-1
0 

 

样例解释
时刻 1，第 1 个任务被分配到第 1 台计算机，耗时为 5，这个任务时刻 6 会结束，占用计算机 1 的算力 3。

时刻 2，第 2 个任务需要的算力不足，所以分配失败了。

时刻 3，第 1 个计算机仍然正在计算第 1 个任务，剩余算力不足 3，所以失败。

时刻 4，第 1 个计算机仍然正在计算第 1 个任务，但剩余算力足够，分配后剩余算力 1。

时刻 5，第 1 个计算机仍然正在计算第 1,4 个任务，剩余算力不足 4，失败。

时刻 6，第 1 个计算机仍然正在计算第 4 个任务，剩余算力足够，且恰好用完。

 1、思路怎么想？

 

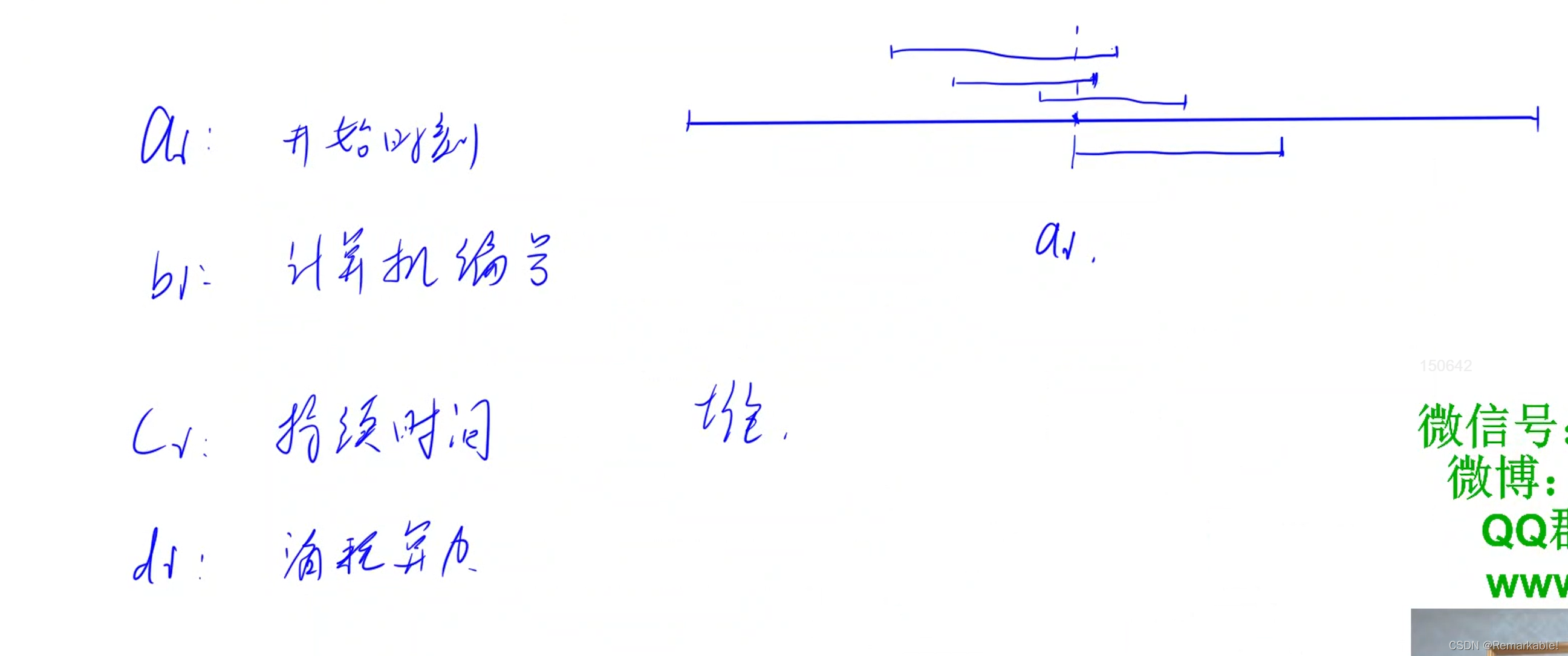
（1）目的是当一个新的任务进来后，每次需要判断当前计算机的剩余算力够不够，

范围是20万，所以时间需要控制到O(nlogn)以内

（2）所以，我们只需维护一下当前ai这个时刻，计算机消耗的资源是多少，剩余的算力是多少，

（3）那么怎么维护？

按顺序枚举每个起点，

我们需要把所有终点在当前起点ai之前的所有区间删掉（随时更新计算机的算力），

（4）那么，怎么删？

用一个堆来维护这个过程，每次找到还没有被删掉的区间里边右端点最小的一个，如果右端点比当前起点ai小的话，就要删去，

所以，实质就是用一个优先队列维护，找最小值的操作，删最小值的操作，

（5）总述，每次来一个任务后，把开始之前的任务全部删掉，之后再把新任务加进来，每次操作只维护计算机当前剩余的算力总值，

2、代码怎么写？

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#define x first 
#define y second  

using namespace std;

const int N = 200010;

typedef pair<int , int> PII;//<任务结束时刻,消耗的算力>

int n , m;
int s[N];//存储计算机的当前算力 
priority_queue<PII , vector<PII> , greater<PII>> q[N];//小根堆

int main()
{
	scanf("%d%d", &n , &m);
	for(int i = 1 ; i <= n ; i++) scanf("%d", &s[i]);
	while(m--)
	{
		int a , b , c , d;
		scanf("%d%d%d%d" , &a ,&b , &c ,&d);
		//维护
		while(q[b].size() && q[b].top().x <= a)//最小的右端点小于a 
		{
			s[b] += q[b].top().y;
			q[b].pop(); 
		} 
		if(s[b] < d) printf("-1\n");
		else
		{
			q[b].push({a + c , d});//将新的任务加入
			s[b] -= d;
			printf("%d\n" , s[b]);	
		} 	
	}
	return 0;
}