深度学习的实用层面

1、训练、验证、测试集的划分

        在配置训练、验证、测试数据集的过程中，通过做出正确的决策可以帮助创建一个高效的神经网络，这些决策包括但不限于：神经网络包含多少层、每层包含多少隐藏单元、学习速率是多少、各层采取哪些激活函数。

        通常在项目开始时，我们会有一个初步的想法，比如构建一个含有特定层数、隐藏单元以及数据集的神经网络，然后进行编码，并根据得出的结果来完善自己的想法，改善策略，或者为了找到更好的神经网络不断迭代更新自己的方案。

        通常情况下，从一个领域或者应用领域积累的直觉经验，比如从图像处理到自然语言处理，通常无法直接转移到其他应用领域，最佳决策取决于所拥有的数据量，输入特征的数量、CPU GPU等诸多因素。对于很多应用系统，即使是经验丰富的专家也不可能一开始就设置出非常合适的超参。因此，应用深度学习是一个典型的迭代过程，需要多次的循环往复才可能找到一个称心的神经网络，因此，循环过程中的效率是决定项目进展的一个重要因素。

        高质量的训练集、验证集和测试集是提高循环效率的一种重要的手段。当样本数量较小时，可以依据6、2、2占比进行划分。对于数据量过百万的应用，训练集可以占比99.5%，验证集和测试集各占0.25%，或者验证集0.4%，测试集0.1%。其中测试集设置的目的是为了做出无偏估计，如果不需要无偏估计的话可以不设置测试集。最好保证验证集和测试集的数据来自同一分布。

2、偏差和方差

        偏差和方差是两个易学难精的概念，理解两者的关键数据是训练集误差和验证集误差。初始模型完成后，首先需要知道算法的偏差高不高，如果偏差较高，试着评估训练集或者训练数据的性能，但如果偏差很高的话，那么需要做的就是尝试训练一个新的神经网络，比如包含更多隐藏层或隐藏单元的网络，或者花费更多的时间来训练网络，或者尝试更多的优化算法。最重要的是需要反复去尝试，这个过程可能有用也可能没用，不过通常情况下采取更大的神经网络都会有所帮助，延长训练时间不一定有用，但也并没有什么坏处。不断在训练算法时尝试这些方法，至少结果能较好的拟合训练集数据，这是最低的标准。

        一旦偏差降低到了一个合适的范围，这时候来看一下方差有没有问题，评估方差需要用到验证集的数据，如果方差过高，最好的方法就是采集更多的数据，当然很多情况下实施起来比较的困难，也可以通过正则化来解决过拟合问题。

       需要注意的是：其一，高偏差和高方差是两种完全不同的情况，故解决方法也可能完全不同，一般通过训练集和验证集来确定算法是否存在高方差或高偏差问题，然后根据结果来尝试部分方法。其二；注意偏差和方差两者之间的权衡，只要正则适中，那么构建一个更大的网络便可以在不影响方差的同时减少偏差，而采用更多的数据可以在不影响偏差的同时降低方差。

3、正则化

       深度学习中存在的过拟合问题，一般有两种解决方法，一种是增加数据量，另一种是更为简便的方法——正则化。为什么正则化可以减少过拟合呢？直观上理解就是如果正则化系数设置的足够大，权重矩阵W会被设置为接近于0的值，即把多个隐藏单元的权重设为0，基本消除了这些隐藏单元的许多影响。该情况下，这个被大大简化了的神经网络就会变成一个很小的网络，小到如同一个逻辑回归单元，但是深度却很大，它会使这个网络从过度拟合的状态更接近高偏差状态。正则化系数从零到足够大之间会存在一个中间值，使得模型处在“刚刚好”的状态。增大lamda的过程就是减小神经网络所有隐藏单元的过程，使得神经网络变得相对更简单了。

常用的正则化有：

• L2正则化：缺点是需要尝试大量的正则化系数的值，计算代价太高；
• dropout正则化（即随机失活，主要应用在计算机视觉领域，其最大的缺点就是代价函数J不再被明确定义，每次迭代，都会随机移除一些节点，如果想检查梯度下降的性能，实际上是很难进行复查的）；
• 数据扩增：对原始图片进行随机翻转、随意放大后剪裁等；
• Early stopping：即在运行梯度下降时，对训练误差进行可视化在合适的地方停止梯度下降，或者只绘制代价函数J的优化过程，缺点是不能够独立的来进行这个过程，因为提早停止了梯度下降也就停止了优化代价函数，优点是只需要进行一次梯度下降就可以找出w较小值、中间值和较大值，效率比较高；

4、归一化

       训练神经网络，其中一个加速训练的方法就是归一化，即零化均值、归一标准差，服从标准正态分布。可以加速梯度下降算法。

5、梯度消失和梯度爆炸

       训练神经网络，尤其是深度神经网络时所面临的一个问题就是梯度消失或者梯度爆炸，即训练神经网络时，导数或坡度有时会变得非常大，或非常小，甚至于指数方式变小，增大训练的难度。

       初始权重设置的比单位矩阵略大或者略小，深度神经网络的激活函数就会呈爆炸式变化，其值就会变得极大或极小，从而导致训练难度上升，尤其是梯度指数很小的时候，梯度下降算法的步长会非常非常小，大大增加训练花费的时间。

       一个解决的方法是针对不同的激活函数设置不同的初始权重，比如Relu函数方差设为2/n就比较好。

6、梯度检验

       梯度检验的目的是为了保证backprop的正确实施，因为实际操作中很难保证backprop每一步都是100%正确的。

在执行梯度检验时，使用双边误差会比较好，因为它比单边误差更为精确，即:

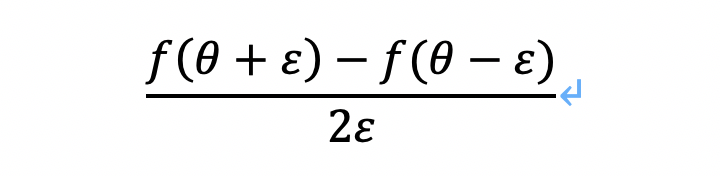
6.1 梯度检验的具体步骤：

• 首先将所有参数w1和b1……wL和bL转换成一个巨大的向量数据，即把矩阵W转换成一个向量之后做连接运算得到一个巨型向量Θ，由于代价函数J是所有w和b的函数，故现在得到一个关于参数Θ的代价函数J(Θ)。
• 接着同样可以把dw1和db1……dwL和dbL初始化成大向量dΘ，它与Θ具有相同的维度。

利用上面的双边误差计算公式计算误差，正常情况下它应该逼近J(Θ)对Θ的偏导数，通过判断这些向量是否彼此接近来进行梯度检验，其中：

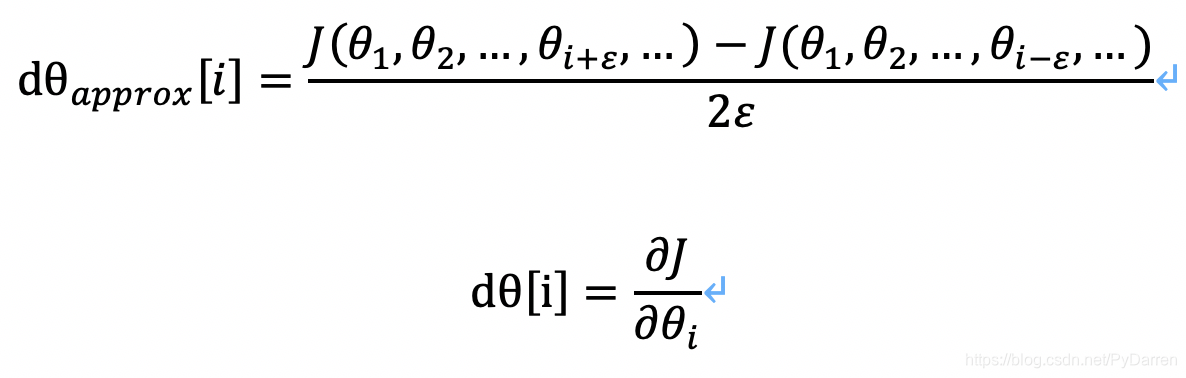
• 通过计算两者的欧式距离（误差的平方和再求平方根），如果最后得到的ε为10-7或者更小，说明导数逼近很有可能是正确的，因为其值很小；如果为10-5，则需要引起注意，也许没有问题，也许有bug；如果为10-3，则需要进一步通过调试来检验。

6.2 梯度检验中的注意事项

• 不要在训练中执行它，仅仅将其应用于调试；
• 如果算法的梯度检验失败，要检查所有项，检查每一项，并试着找出bug，即查找不同的i值，看看是哪一项导致了两者的差距变大的；
• 如果代价函数中包含了正则项，记得一定不能忽略；
• 梯度检验不能与dropout共同使用，因为每次的迭代过程中，dropout会随机消除隐藏层单元的不同子集，难以计算代价函数；
• 最后一点比较微妙，现实中可能并不存在这种情况。在w和b接近0的时候，梯度下降的实施是正确的，但在运行梯度下降时，w和b会变得更大，会变得越来越不准确，一种比较少见的做法是在初始化训练过程中，运行梯度检验，从而解决w和b一段时间后远离0的问题，循环反复这个过程。