一、深度学习与深层神经网络
深度学习的精确定义——一类通过多层非线性变换对高复杂性数据建模算法的合集。深层神经网络实际上有组合特征提取的功能,对于不易提取特征向量的问题(比如图片识别、语音识别等)有很大帮助,故可以解决异或问题,同时这也是深度学习能够在图像、语言等方向取得突破性进展的原因。这里涉及到几个概念:
- 多层和非线性
这是深度学习两个非常重要的特性。线性模型的局限性在于任意线性模型的组合仍然还是线性模型。只通过线性变化,任意层的全连接神经网络和单层神经网络的表达能力没有任何区别,而且它们都是线性模型。
- 复杂问题
所谓复杂问题,至少是无法通过线性可分的,现实世界的绝大多数问题都不是线性可分的。
通过激活函数实现去线性化:
当每一个神经元节点的输出通过一个非线性函数时,那么整个神经网络的模型就不再是线性了。常见的激活函数有ReLU、sigmoid和tanh函数。
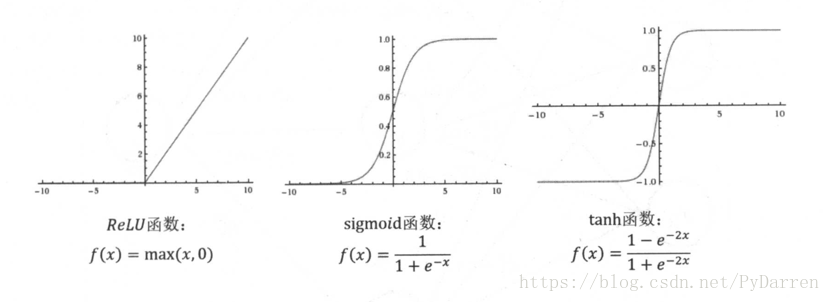
以ReLU为例,TensorFlow中很好的支持了激活函数和偏置项:
1. a= tf.nn .relu (tf.matmul(x, wl) + biasesl)
2. y = tf.nn.relu(tf.matmul(a, w2) + biases2)
二、损失函数
神经网络模型的效果以及优化的目标是通过损失函数来定义的。二分类问题中通常用0.5作为阈值,但是很难直接推广到多分类问题中。多分类问题中通常是设置n(类别个数)个节点,这样每次输出为一个n维数组,数组中的每一个维度对应一个类别。以识别数字1为例,模型输出越接近[0,1,0,0,0,0,0,0,0,0]越好。判断一个输出向量与期望向量之间接近程度通常用交叉熵。交叉熵刻画了两个概率分布之间的距离,它是分类问题中使用比较广的一种损失函数。
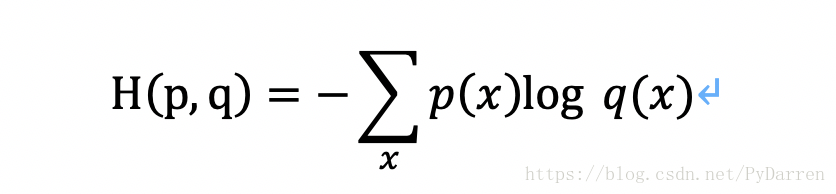





 本文介绍了深度学习的基础,包括深度神经网络的非线性和复杂问题解决,讲解了激活函数如ReLU的作用。讨论了损失函数,特别是交叉熵在多分类问题中的应用,并提到了自定义损失函数的可能性。此外,还阐述了反向传播和梯度下降在神经网络优化中的作用,以及学习率设置的重要性。最后,探讨了解决过拟合问题的正则化技术,如L1和L2正则化。
本文介绍了深度学习的基础,包括深度神经网络的非线性和复杂问题解决,讲解了激活函数如ReLU的作用。讨论了损失函数,特别是交叉熵在多分类问题中的应用,并提到了自定义损失函数的可能性。此外,还阐述了反向传播和梯度下降在神经网络优化中的作用,以及学习率设置的重要性。最后,探讨了解决过拟合问题的正则化技术,如L1和L2正则化。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 654
654

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








