正则化L1，L2

一、正则化的本质：“给模型加约束，避免过拟合”

在机器学习中，模型过拟合的本质是参数过于复杂（比如权重w的值过大或过于 “极端”），导致模型 “记住” 了训练数据的噪声。

正则化的核心是在损失函数中加入 “惩罚项”，限制参数的复杂度，从而平衡 “拟合能力” 和 “泛化能力”。

---

二、L2 正则化（权重衰减，Ridge Regression）

1. 数学形式

在损失函数中加入参数的平方和，

形式如下：

• λ：正则化强度参数（λ越大，惩罚越强）；
• m：样本数量；
• wj​：模型的权重参数（对偏置b一般不做正则化）。

2. 直观理解：“让权重尽可能小，模型更平滑”

L2 正则化会惩罚大的权重值，迫使权重向 0 靠近（但不会完全为 0）。比如线性回归中，L2 正则化会让模型的 “曲线 / 直线” 更 “平滑”，避免因个别样本的噪声而剧烈波动。

举个例子：假设模型是预测房价，特征包括 “面积”“卧室数”“距离地铁站的距离” 等。

L2 正则化会让每个特征的权重都比较小，模型不会过度依赖某一个特征（比如不会因为 “卧室数” 的微小变化就大幅改变房价预测）。

3. 优化角度：“解的稳定性”

从优化理论看，L2 正则化相当于给参数空间加了一个“球面约束”（因为是球面）。在这种约束下，损失函数的最优解会更 “稳定”—— 即使训练数据有小的扰动，参数的变化也不会太大，从而提升泛化能力。

4. 适用场景

• 数据维度高、样本量少，容易过拟合的场景（比如基因数据、文本特征）；
• 希望所有特征都对模型有 “温和” 贡献，不希望某几个特征主导预测的场景；
• 后续需要解释模型（因为权重不会为 0，所有特征都有一定作用，便于分析）。

---

三、L1 正则化（Lasso Regression）

1. 数学形式

在损失函数中加入参数的绝对值和，

形式如下：

（注意：L1 的正则项系数通常是λ​/m，和 L2 的λ​/2m形式略有不同，是为了优化时的数学便利）

2. 直观理解：“让不重要的特征权重直接为 0，实现特征选择”

L1 正则化的独特之处是会把很多不重要的特征的权重压缩到 0。

比如还是预测房价的例子，L1 正则化可能会直接让 “距离地铁站的距离” 这个特征的权重为 0，模型不再考虑它 —— 相当于自动完成了 “特征选择”，只保留最关键的特征。

3. 优化角度：“解的稀疏性”

从优化理论看，L1 正则化相当于给参数空间加了一个“立方体约束”（因为是立方体）。立方体的 “角点”（即某些wj​=0的点）更容易成为最优解，这就是 L1 能产生 “稀疏解”（很多权重为 0）的原因。

4. 适用场景

• 特征维度极高，需要筛选出关键特征的场景（比如文本分类中，词汇表有几万个词，L1 能选出最有区分度的词）；
• 希望模型 “简洁高效”，只保留核心特征的场景；
• 数据中存在大量冗余或无关特征的场景。

---

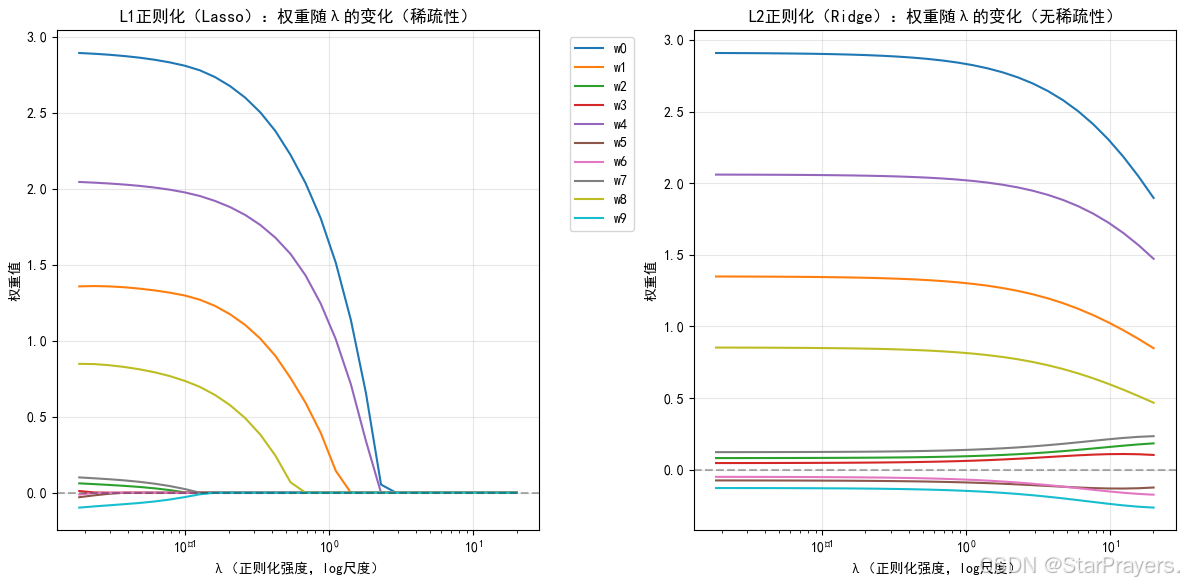
四、L1 vs L2：核心区别对比

维度	L2 正则化（Ridge）	L1 正则化（Lasso）
数学形式	权重的平方和	权重的绝对值和
对权重的影响	权重缩小但不为 0	权重可能被压缩为 0
优化后的解	所有特征都有贡献（无稀疏性）	仅关键特征有贡献（稀疏性）
适用场景	需保留所有特征、防过拟合	需筛选特征、简化模型
计算复杂度	低（优化时可求导，计算稳定）	高（绝对值不可导，需特殊优化方法如坐标轴下降）

---

五、扩展：弹性网络（Elastic Net）——L1+L2 的结合

为了结合 L1 和 L2 的优点，还可以使用弹性网络，

其正则项是 L1 和 L2 的加权组合：

它既能像 L1 一样实现特征选择，又能像 L2 一样保证优化的稳定性，适合对稀疏性和泛化能力都有要求的场景。