Advances in Graph Neural Networks笔记5：Dynamic Graph Neural Networks

最新推荐文章于 2024-03-04 17:16:51 发布
原创 最新推荐文章于 2024-03-04 17:16:51 发布 · 820 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#图神经网络 #GNN #动态图神经网络 #动态图 #图论

本文介绍了动态图GNN的关键技术，包括M2^22DNE、HPGE和DyMGNN等方法。M2^22DNE利用时间点过程来建模动态图中的边的形成；HPGE关注于动态异质图的学习；而DyMGNN则通过动态元路径引导的时间异质图模型来捕获动态语义。

诸神缄默不语-个人优快云博文目录

本书网址：https://link.springer.com/book/10.1007/978-3-031-16174-2
本文是本书第五章的笔记。
懒得看了！反正我也不是做这个的。以后要是真的去做动态图了也不是没资源找，这个我懒得看了，就写一半算了，目测不会更新，如果我改做动态图而且拿到全书资源了可能会更新。

文章目录

1. 动态图GNN概念介绍

捕获动态图时间演变的常用方法：将整图分割为多个snapshots，分别嵌入得到snapshot-based embeddings，用LSTM / GRU等序列模型生成表征。

动态图时间演变常包含两个动态过程：

  1. the microscopic dynamics of edge establishments
  2. macroscopic dynamics of network scales

2. M 2 ^2 2DNE

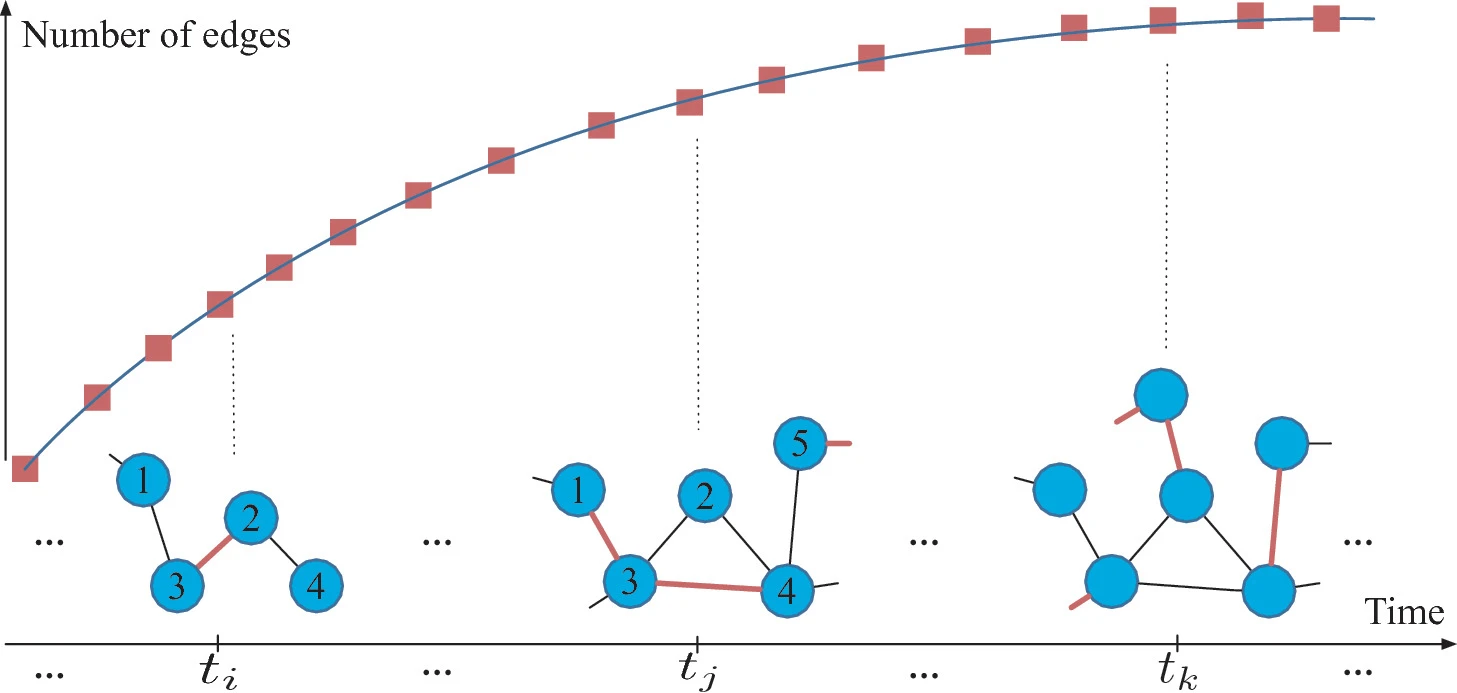
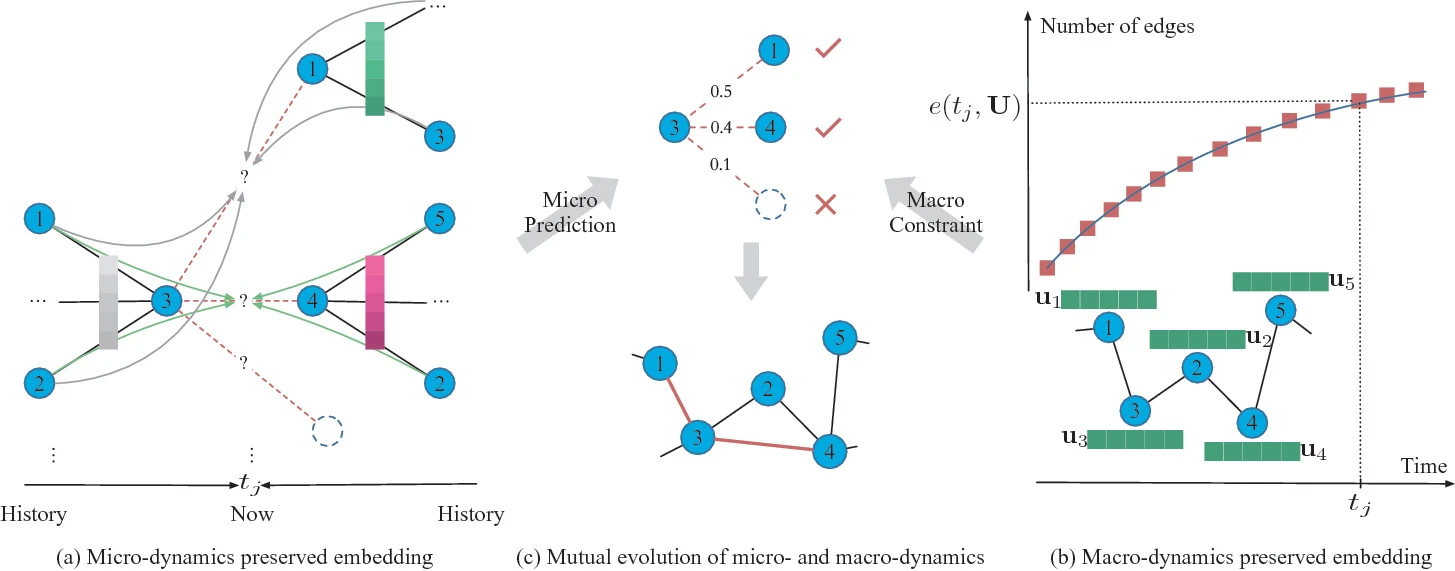
基于temporal point process建模边的宏微观动态。

微观：边渐渐形成。更近的边影响更大
宏观：网络尺寸的演进遵循显著分布，如S-shaped sigmoid curve或power-law-like pattern
在这里插入图片描述

M 2 ^2 2DNE
在这里插入图片描述

3. HPGE：动态异质图

学习所有异质动态事件的形成过程，保留语义和动态
（事件就是指某个时间点，两个节点之间多长一条边）

Heterogeneous Hawkes Process

4. DyMGNN

dynamic meta-path guided temporal heterogeneous graph modeling approach

设计dynamic meta-path and heterogeneous mutual evolution attention mechanisms，有效捕获dynamic semantics，建模mutual evolution of different semantics

[论文解读]All in one：: Multi-Task Prompting for Graph Neural Networks图神经网络的多任务提示
强化学习曾小健
02-26 2179
这个函数可能是对提示图参数进行操作的某种计算，比如根据这些参数生成新的节点表示，或者更新模型的状态以适应新任务。在不同的上下文中，函数 f(θ) 可以有不同的具体含义，它通常会涉及到如何使用这些参数来影响模型的行为或其对数据的处理方式。不过，由于我无法直接查看PDF文件的内容，所以这里的解释是基于常见的机器学习和深度学习术语的一般性解释。提示图是一种用于调整预训练模型以适应特定任务的结构，这些参数可能包括用于构造提示的节点和边的权重，或者其他用于定义提示图结构的属性。与原始图 G 结合后的新表达式。
Graph Neural Networks: A Review of Methods and Applications（图神经网络：方法与应用综述）
weixin_41697507的博客
07-06 5896
Graph Neural Networks: A Review of Methods and Applications Jie Zhou , Ganqu Cui , Zhengyan Zhang , Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, Maosong Sun Abstract—Lots of learning tasks req...
Dynamic Graph Neural Networks for Sequential Recommendation
且视他人之疑目如盏盏鬼火,大胆地去走你的夜路
06-01 3281
一个月前刚出的论文，占领第一片土地！ 基于动态图卷积神经的序列化推荐系统 摘要 从用户的历史序列中建模用户偏好是顺序推荐的核心问题之一。这些领域的现有方法从传统方法到深度学习方法分布广泛。然而，它们大多只在自己的序列中建模用户兴趣，而忽略了不同用户序列之间动态协作信号的细粒度利用，不足以探索用户偏好。我们从动态图神经网络中获得灵感来应对这一挑战，将用户序列建模和用户之间的动态交互信息统一到一个框架中。提出了一种新的动态图神经网络顺序推荐方法(DGSR)，该方法通过动态图结构连接不同用户的顺序，探索具有时.
Dynamic Graph Learning-Neural Network for Multivariate Time Series Modeling
小蚂蚁与大象
06-02 571
Dynamic Graph Learning-Neural Network for Multivariate Time Series Modeling 摘要：多元时间序列预测是一项具有挑战性的任务，因为数据涉及长期和短期模式的混合，变量之间具有动态的时空相关性。现有的图神经网络(GNN)通常用预定义的空间图或学习到的固定邻接图来建模多元关系。它限制了GNN的应用，无法应对上述挑战。在本文中，我们提出了一个新的框架，即静态和动态图学习神经网络(SDGL)。该模型从数据中获取静态和动态图矩阵，分别对长期和短期
【推荐系统-＞论文阅读】Dynamic Graph Neural Networks for Sequential Recommendation（用于序列推荐的动态图神经网络）
小明2766的博客
04-15 3655
Dynamic Graph Neural Networks for Sequential Recommendation（用于序列推荐的动态图神经网络） Mengqi Zhang, Shu Wu,Member, IEEE,Xueli Yu, Qiang Liu,Member, IEEE,Liang Wang,Fellow, IEEE 文章目录Dynamic Graph Neural Networks for Sequential Recommendation（用于序列推荐的动态图神经网络）Abstract（
TodyNet: Temporal Dynamic Graph NeuralNetwork for Multivariate Time Series Classification
qq_46474804的博客
03-04 1793
本文提出了一种新的时间动态图神经网络（TodyNet），可以在没有预定义图结构的情况下提取隐藏的时空依赖关系。它使得信息能够在孤立但隐式相互依赖的变量之间流动，并通过动态图机制捕捉不同时间段之间的关联，进一步提高了模型的分类性能。与此同时，由于图神经网络（GNNs）的限制，无法学习图的分层表示。因此，我们还设计了一个时间图池化层，以获取具有可学习时间参数的全局图级表示，用于图的学习。动态图、图信息传播和时间卷积在一个端到端的框架中共同学习。
GNN动态顺序推荐Dynamic Graph Neural Networks for Sequential Recommendation
记录学习历程
09-13 1196
为了更新每一层的用户节点表示，需要从每个用户节点的邻居中提取两种类型的信息，分别是长期偏好和短期偏好。此时用户兴趣变化不仅受到自身交互商品(一阶交互项)变化的影响，还受到高阶连接的用户和他们交互的商品的变化的影响，随时间变化。考虑到用户序列扩展时，其邻居序列的数量在不断增加，所有用户组成的动态图的规模在逐渐扩大，会增加计算量和噪声，因此提出采样策略。（1）这些模型没有利用不同用户序列之间的协作信息，仅仅侧重于每个用户自己的序列，忽略了不同用户序列之间的高阶连通性。不同层次的用户嵌入强调了用户的不同偏好。
GNNExplainer: Generating Explanations for Graph Neural Networks 个人总结
vincent_x3的博客
04-27 3602
GNNExplainer: Generating Explanations for Graph Neural Networks 个人总结 写在前面：为方便阅读，尽量使用中文总结，对于翻译无把握或专有词汇，在中文后附上原文字段。此外，水平有限，对文章理解有偏差部分恳请大家海涵, 指正。 0. 原作信息 @inproceedings{ying2019gnnexplainer, title={G...
文献阅读（03）Computing Graph Neural Networks: A Survey from Algorithms to Accelerators
m0_60300581的博客
01-07 1656
作者：SERGI ABADAL, AKSHAY JAIN, ROBERT GUIRADO, JORGE LÓPEZ-ALONSO, and EDUARD ALARCÓN 目录 文章脉络： 缩写&&引用： 关于gnns算法及其应用的文献： GNNs的本质、难点简介： 本质： 难点： 目前所作的尝试： 文章脉络： 本文是关于图神经网络的一篇综述。内容主要包括：图神经网络的概念；图神经网络的发展以及演变；关于图神经网络的加速器部分；最后是关于图神经网络在加速器中的架构设..
Graph Neural Networks_ A Review of Methods and Applications----清华大学周杰.pdf
09-03
Gated Graph Neural Networks (GGNNs):** GGNNs utilize gating mechanisms similar to those found in recurrent neural networks (RNNs) to control the flow of information during the message passing phase....
文献阅读（55）arXiv2021-Pre-Training on Dynamic Graph Neural Networks
优快云TianJi的博客
10-11 856
本文是对《Pre-Training on Dynamic Graph Neural Networks》一文的浅显翻译与理解，如有侵权即刻删除。
论文导读 | 动态图上神经网络模型综述
weixin_48167662的博客
12-15 6996
北京大学 李荆 编者按： 原文《Foundations and modelling of dynamic networks using Dynamic Graph Neural Networks: A survey》介绍一篇关于动态图上的神经网络模型的综述，本篇综述的主要结构是根据动态图上进行表示学习过程的几个阶段（动态图表示、模型学习、模型预测）进行分别阐述。包括 1. 系统的探讨不同维度下的动态图分类方法以及各种方法下的数据表示格式 2. 针对不同类别的动态图归纳目前图表示学习的主流算法模型..
动态图神经网络
weixin_44370695的博客
06-21 1588
我们提出的方法可以有效地通过发现和处理动态图中的时空分布变化充分利用不变的时空格局。最后，我们提出了一个不变性正则化项来最小化干预分布中预测的方差，这样我们的模型就可以基于不变模式的预测，具有稳定的预测能力，因此可以处理分布变化。在三个真实世界的数据集上做实验。在本文中，我们建议处理动态图时空分布的发现与利用不变模式，即预测能力稳定的结构和特征这面临着两个关键的挑战:1)如何发现动态图中复杂的变化与不变的时空模式同时涉及时变图结构和节点特征。我们的工作是对时空的首次研究，据我们所知，分布在动态图形中变化。
2023.2.9，周四【图神经网络 学习记录22】动态图算法 之 EvolveGCN：离散型动态GNN网络，将GNN和RNN结合到同一层，结合时间和空间信息进行建模
追光者♂：记录、分享、总结、提升，现象级专栏《Python从入门到人工智能》作者，无惧黑暗，坚信曙光
02-09 788
【图神经网络 学习记录22】动态图算法 之 EvolveGCN：离散型动态GNN网络，将GNN和RNN结合到同一层，结合时间和空间信息进行建模
图神经网络（GNN）
博主关注人工智能、强化学习、嵌入式等||985高校A+学科研究生、猿龄六年||优快云博客专家、2024年博客之星TOP33、华为云享专家、人工智能领域优质创作者。
08-07 1409
图不但包含数据，也包含数据之间的依赖关系，因而图神经网络（GNN）在自然语言处理（NLP）方面的表现有着非常大的潜力。图神经网络（GNN）最擅长处理和建模图结构数据。 GNN的工作原理简单概况就是，聚合节点的邻居节点/边的信息，来更新节点的向量表征。 ​
动态图snapshot构建
菜鸡小陈的博客
03-10 583
让我们构建一个由 5 个人组成的小型社交网络图（见图 1）。这里的节点代表人，边代表两个人之间的友谊。这就是 T = 0 时的情况。当它们相互影响一段时间时，可以形成一些新的关系，也可以打破一些新的关系。另外，请记住，新人可以在任何时间点进入此社交网络，现有成员也可以离开。 在社交网络的演化过程中，我们在 3 个时间点获得了 3 个snapshot。所有这 3 个snapshot构成了动态图。我们目睹了一些新的友谊正在建立，也有一些被打破。我们可能会遇到新的传入节点（加入网...
【GNN】首篇NLP领域图神经网络综述：127页，从图构建到实际应用面面观
AI蜗牛车
07-14 901
作者：Lingfei Wu等编译：机器之心编辑：Panda在 Transformer 推动自然语言处理领域迅猛发展的当下，基于图神经网络的 NLP 研究也不容忽视。在近日的一篇综述论文中，...
面向动态图的极低时延 GNN 在线推理采样服务
graphscope的博客
08-05 590
本文主要介绍 GraphScope 图学习引擎 GraphLearn 最新推出的面向 GNN 在线推理任务的动态图采样服务。
从几篇综述区分Dynamic Graph和Spatial-temporal Graph
羊城迷鹿的博客
02-28 8131
Foundations and modelling of dynamic networks using Dynamic Graph Neural Networks: A survey 本文首先给出了动态网络的定义和分类，然后分别从编码和解码的角度介绍了图神经网络模型如何用于动态图的嵌入表示以及完成链路预测任务 动态网络 定义 动态网络是随时间变化的复杂网络。链接和节点可能出现和消失。 一个 动态网络可以表示为一个图G=(V,E)G=(V, E)G=(V,E)，其中V={(v,ts,te)}V=\{(v
Neural ODEs神经常微分方程神经网络流程图
最新发布
11-13
<think> 我们正在讨论Neural ODEs（神经常微分方程神经网络）。用户要求流程图，但请注意，流程图通常以图形方式呈现，而文本描述可能不够直观。不过，我们可以用文字描述流程图的主要步骤，并尝试用Mermaid语法绘制一个简单的流程图（如果支持的话）。但请注意，当前环境可能不支持渲染Mermaid图表，因此我将提供文字描述和Mermaid代码，用户可以在支持Mermaid的环境中查看。 Neural ODEs的核心思想是将神经网络视为一个连续动态系统，使用常微分方程（ODE）来建模数据的变换。其关键步骤如下： 1. **输入数据**：输入向量（例如，一个图像的特征向量）。 2. **定义ODE**：使用一个神经网络（称为ODE函数）来定义隐藏状态的导数：$dh(t)/dt = f(h(t), t, \theta)$，其中$f$是由神经网络参数化的函数。 3. **数值求解ODE**：使用ODE求解器（如欧拉法、Runge-Kutta等）从初始状态$h(t_0)$（即输入）开始，求解到期望的终点$h(t_1)$，得到输出。 4. **输出结果**：ODE求解器的输出就是神经网络的输出。 训练过程则通过伴随灵敏性方法（adjoint sensitivity method）来高效计算梯度，避免存储中间状态。 下面我们用Mermaid语法描述流程图： ```mermaid graph TD A[输入 h0] --> B[定义ODE: dh/dt = f h t θ] B --> C[使用ODE求解器求解 h1 = ODESolve f, h0, t0, t1] C --> D[输出 h1] D --> E[计算损失函数 L] E --> F[通过伴随方法计算梯度 dL/dθ] F --> G[更新参数 θ] ``` 但是，由于我们无法在此环境中渲染Mermaid图，我将用文字详细描述： 1. 开始：输入初始状态$h_0$（例如，输入数据）。 2. 定义ODE函数：使用一个神经网络$f$来定义状态$h$随时间$t$的变化率：$\frac{dh(t)}{dt} = f(h(t), t, \theta)$，其中$\theta$是神经网络的参数。 3. 求解ODE：使用数值ODE求解器（如dopri5）从初始时间$t_0$到终止时间$t_1$求解状态，得到$h_1$，即输出。 4. 计算损失：将$h_1$与真实标签比较，计算损失$L$。 5. 梯度计算：使用伴随方法（Adjoint Method）计算损失$L$关于参数$\theta$的梯度。伴随方法定义了一个伴随状态$a(t) = \frac{\partial L}{\partial h(t)}$，并反向求解伴随方程。 6. 更新参数：利用梯度下降法更新参数$\theta$。 注意：在反向传播中，传统神经网络存储中间状态，而Neural ODEs通过求解伴随方程（另一个ODE）来反向计算梯度，从而节省内存。 参考文献：原始论文[^1]（Chen, T. Q., Rubanova, Y., Bettencourt, J., & Duvenaud, D. K. (2018). Neural ordinary differential equations. Advances in neural information processing systems, 31.） §§相关问题§§ 1. Neural ODEs与传统神经网络的主要区别是什么？ 2. 为什么Neural ODEs在反向传播时更节省内存？ 3. Neural ODEs中常用的ODE求解器有哪些？ </think> 以下是关于 Neural ODEs（神经常微分方程神经网络）的流程图描述及核心原理说明： ### Neural ODEs 流程图 ```mermaid graph TD A[输入数据 z0] --> B[定义ODE函数 fz] B --> C[ODE求解器] C --> D[输出 zT = z0 + &int;fz dt<br>t0→T] D --> E[计算损失函数 L] E --> F[伴随状态反向传播] F --> G[参数梯度计算] G --> H[更新神经网络参数 θ] ``` ### 分步说明 1. **输入层** 输入数据 $z_0$（如特征向量或图像） 2. **ODE 函数定义** 通过神经网络定义常微分方程： $$ \frac{dz(t)}{dt} = f(z(t), t, \theta) $$ 其中 $f$ 是参数为 $\theta$ 的神经网络[^1] 3. **前向传播** 使用数值 ODE 求解器计算输出： $$ z_T = z_0 + \int_{t_0}^{T} f(z(t), t, \theta) dt $$ 常用求解器：自适应 Runge-Kutta（如 dopri5） 4. **损失计算** 计算预测输出 $z_T$ 与真实标签的损失 $L$ 5. **反向传播** 通过伴随状态法高效计算梯度： $$ a(t) = \frac{\partial L}{\partial z(t)} \quad ; \quad \frac{d a(t)}{dt} = -a(t)^\top \frac{\partial f}{\partial z} $$ 避免存储中间状态，显著降低内存需求 6. **参数更新** 使用梯度下降更新神经网络参数 $\theta$
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

诸神缄默不语

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值