诸神缄默不语-个人优快云博文目录
cs224w(图机器学习)2021冬季课程学习笔记集合
文章目录
YouTube视频观看地址1 视频观看地址2 视频观看地址3
1. 章节前言
- 传统机器学习pipeline:设计并获取所有训练数据上节点/边/图的特征→训练机器学习模型→应用模型
图数据本身就会有特征,但是我们还想获得说明其在网络中的位置、其局部网络结构local network structure之类的特征(这些额外的特征描述了网络的拓扑结构,能使预测更加准确)
所以最终一共有两种特征:数据的structural feature,以及其本身的attributes and properities1
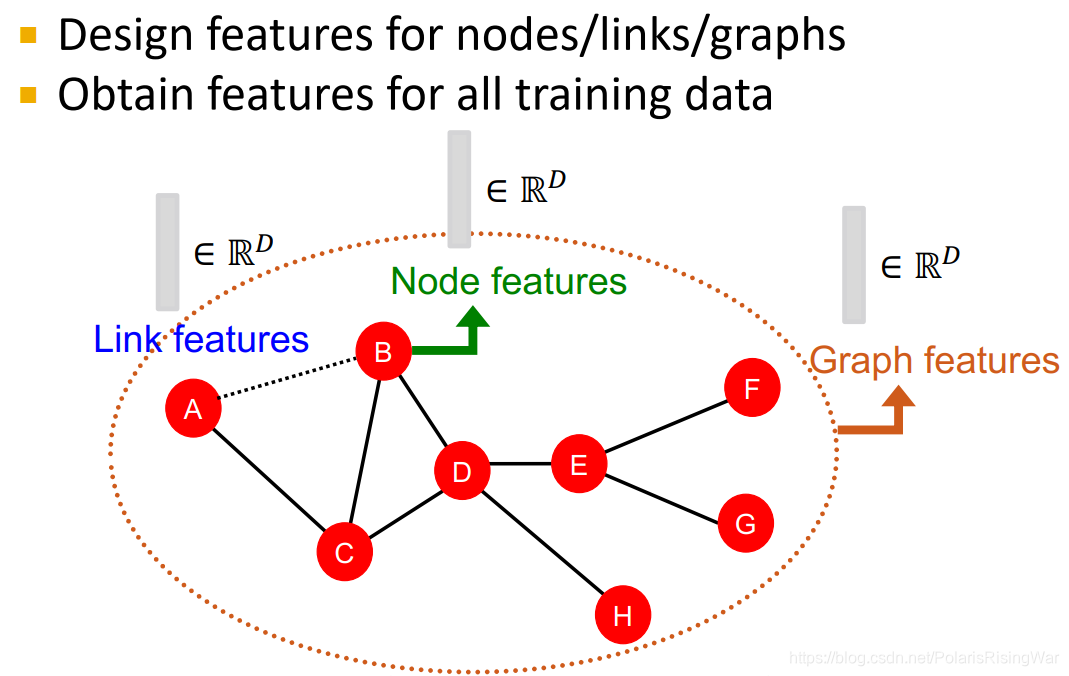
- 本章重点着眼于手工设计无向图三种数据层次上的特征(其relational structure of the network),做预测问题
- 图机器学习的目标:对一系列object做预测
- design choice
- Features: d-dimensional vectors
- Objects: Nodes, edges, sets of nodes, entire graphs
- Objective function: What task are we aiming to solve?
2. Traditional Feature-based Methods: Node
- 半监督学习任务
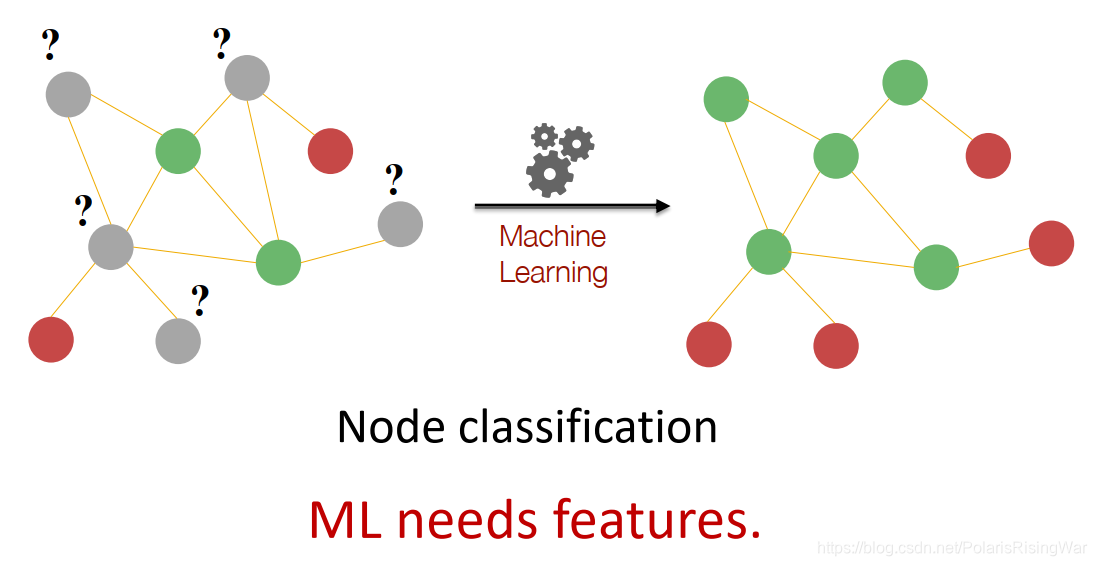 如图所示案例,任务是预测灰点属于红点还是绿点。区分特征是度数(红点度数是1,绿点度数是2)
如图所示案例,任务是预测灰点属于红点还是绿点。区分特征是度数(红点度数是1,绿点度数是2) - 特征抽取目标:找到能够描述节点在网络中结构与位置的特征
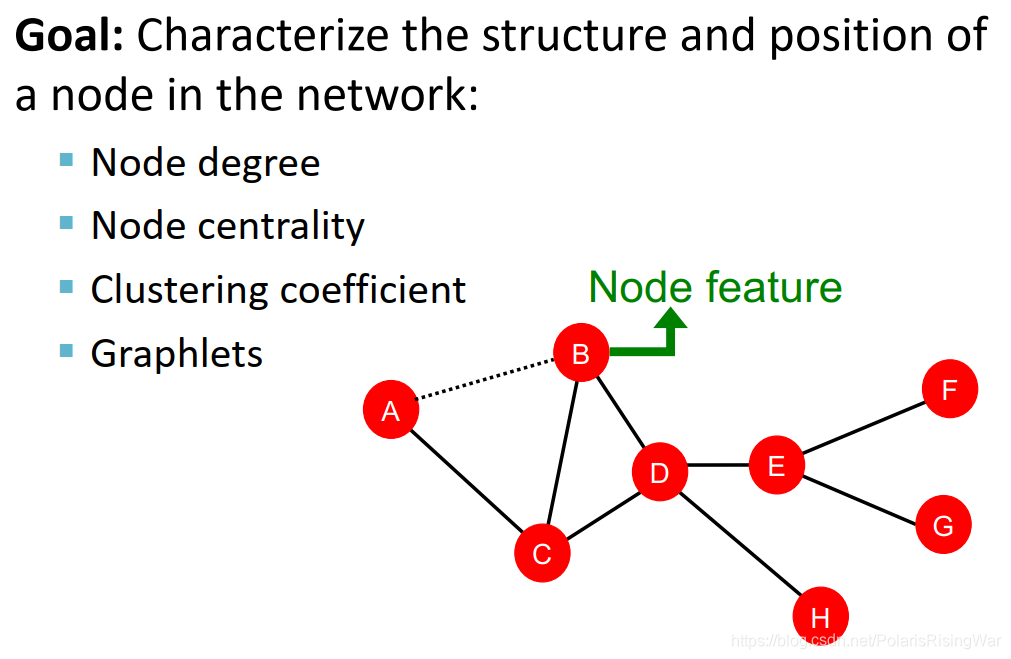
- 度数node degree:缺点在于将节点的所有邻居视为同等重要的
- node centrality
c
v
c_v
cv 考虑了节点的重要性
- eigenvector centrality:认为如果节点邻居重要,那么节点本身也重要
因此节点 v v v 的centrality是邻居centrality的加总: c v = 1 λ ∑ u ∈ N ( v ) c u c_v=\frac{1}{\lambda}\sum\limits_{u\in N(v)}c_u cv=λ1u∈N(v)∑cu ( λ \lambda λ是某个正的常数)
这是个递归式,解法是将其转换为矩阵形式: λ c = A c \lambda \mathbf{c}=\mathbf{Ac} λc=Ac A \mathbf{A} A是邻接矩阵, c \mathbf{c} c是centralty向量。
从而发现centrality就是特征向量。根据Perron-Frobenius Theorem2可知最大的特征值 λ m a x \lambda_{max} λmax 总为正且唯一,对应的leading eigenvector c m a x \mathbf{c}_{max} cmax就是centrality向量 - betweenness centrality:认为如果一个节点处在很多节点对的最短路径上,那么这个节点是重要的。(衡量一个节点作为bridge或transit hub的能力。就对我而言直觉上感觉就像是新加坡的马六甲海峡啊,巴拿马运河啊,埃及的苏伊士运河啊,什么君士坦丁堡,上海,香港……之类的商业要冲的感觉)
c v = ∑ s ≠ v ≠ t # ( s 和 t 之 间 包 含 v 的 最 短 路 径 ) # ( s 和 t 之 间 的 最 短 路 径 ) c_v=\sum\limits_{s\neq v\neq t}\frac{\#(s和t之间包含v的最短路径)}{\#(s和t之间的最短路径)} cv=s=v=t∑#(s和t之间的最短路径)#(s和t之间包含v的最短路径)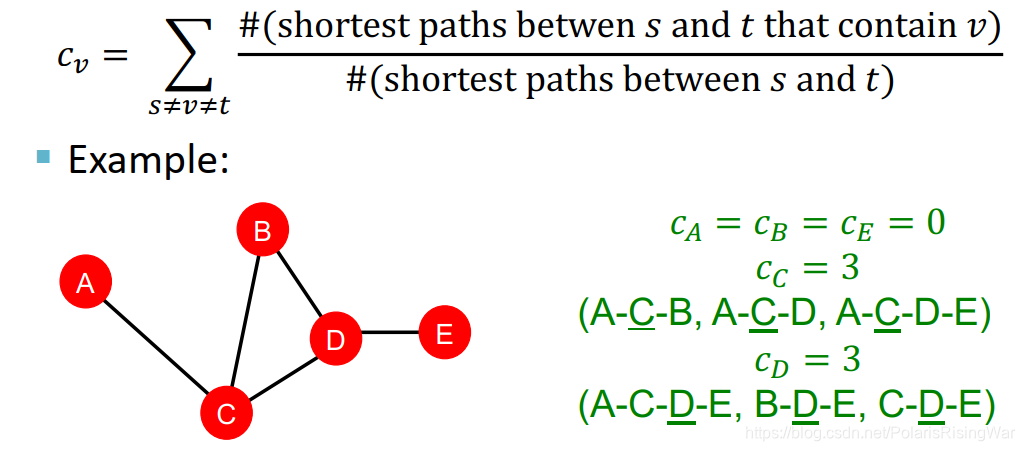 #:the number of…
#:the number of…
图中这个between应该是写错了…… - closeness centrality:认为如果一个节点距其他节点之间距离最短,那么认为这个节点是重要的
c v = 1 ∑ u ≠ v u 和 v 之 间 的 最 短 距 离 c_v=\frac{1}{\sum\limits_{u\neq v}u和v之间的最短距离} cv=u=v∑u和v之间的最短距离1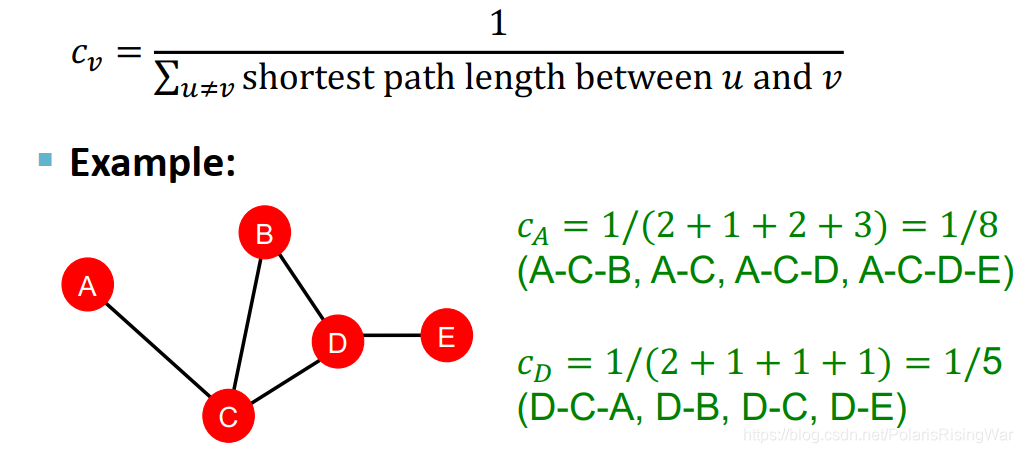
- eigenvector centrality:认为如果节点邻居重要,那么节点本身也重要
- clustering coefficient3:衡量节点邻居的连接程度
描述节点的局部结构信息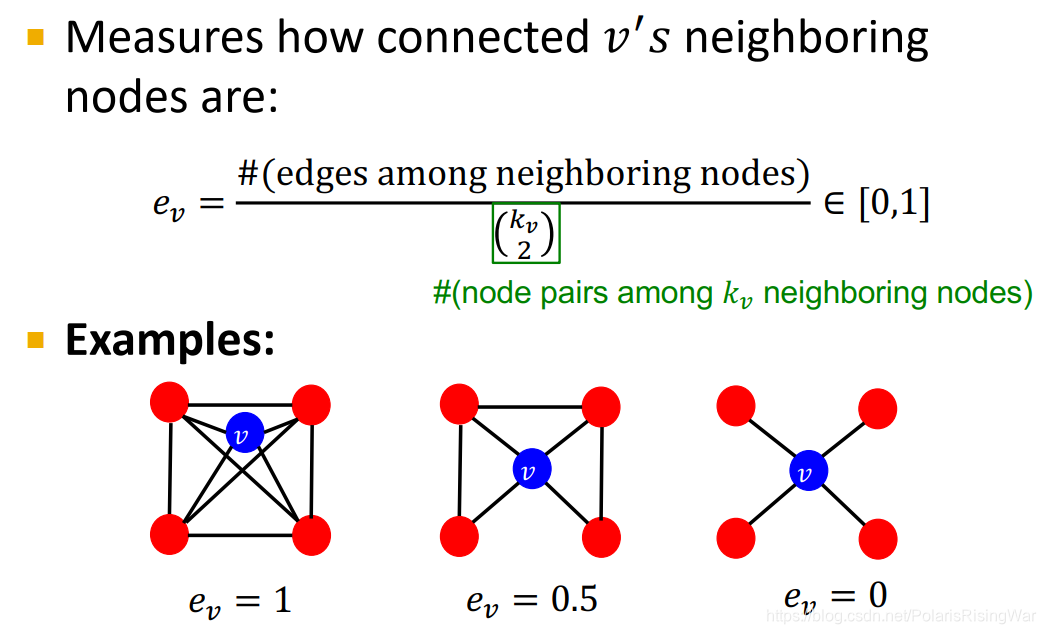 这种
(
k
v
2
)
\begin{pmatrix} k_{v} \\ 2 \end{pmatrix}
(kv2)是组合数的写法,和国内常用的C写法上下是相反的4
这种
(
k
v
2
)
\begin{pmatrix} k_{v} \\ 2 \end{pmatrix}
(kv2)是组合数的写法,和国内常用的C写法上下是相反的4
所以这个式子代表 v v v 邻居所构成的节点对,即潜在的连接数。整个公式衡量节点邻居的连接有多紧密
第1个例子: e v = 6 / 6 e_v=6/6 ev=6/6
第2个例子: e v = 3 / 6 e_v=3/6 ev=3/6
第3个例子: e v = 0 / 6 e_v=0/6 ev=0/6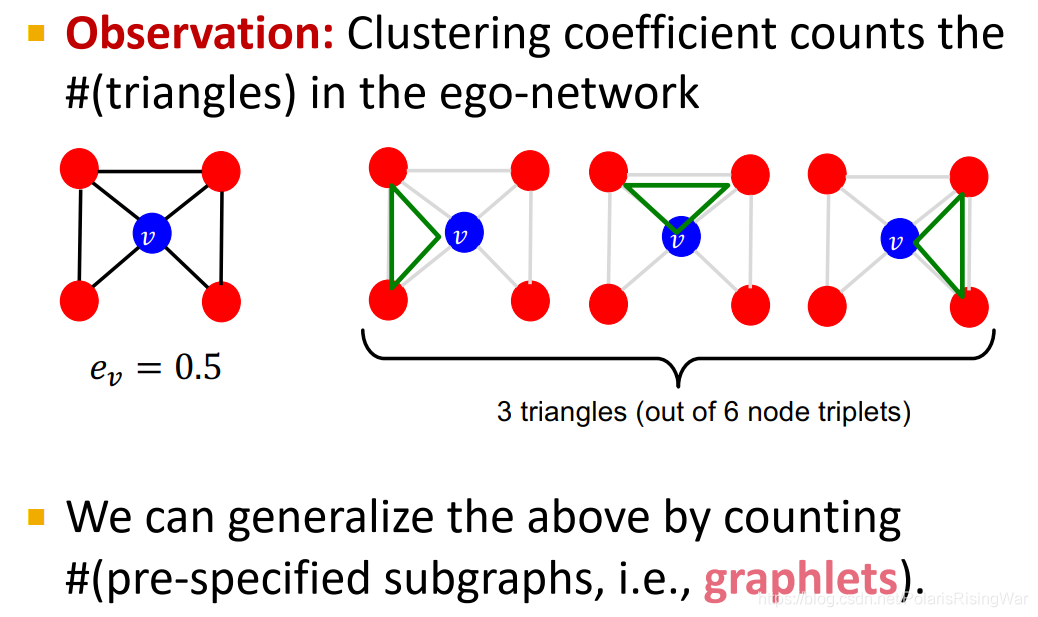 ego-network of a given node is simply a network that is induced by the node itself and its neighbors5. So it’s basically degree 1 neighborhood network around a given node.
ego-network of a given node is simply a network that is induced by the node itself and its neighbors5. So it’s basically degree 1 neighborhood network around a given node.
这种三角形:How manys triples are connected
在社交网络之中会有很多这种三角形,因为可以想象你的朋友可能会经由你的介绍而认识,从而构建出一个这样的三角形/三元组。
这种三角形可以拓展到某些预定义的子图pre-specified subgraph6上,例如如下所示的graphlet: - graphlets有根连通异构子图
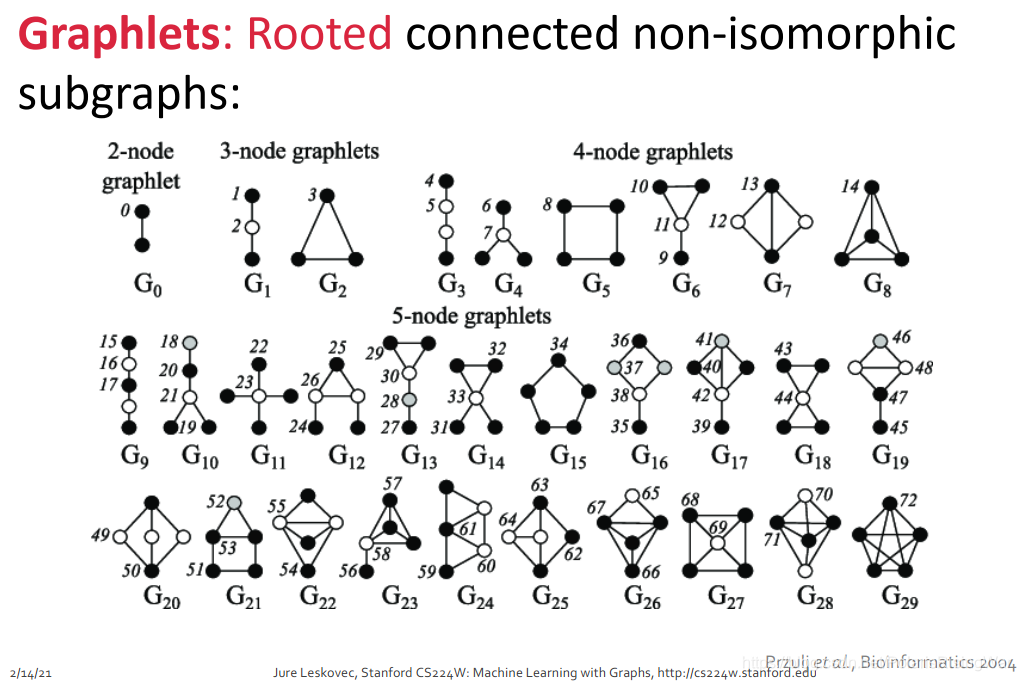
对于某一给定节点数 k k k,会有 n k n_k nk 个连通的异构子图。
就是说,这些图首先是connected的6,其次这些图有k个节点,第三它们异构。
异构,就是说它们形状不一样,就是怎么翻都不一样……就,高中化学应该讲过这个概念,我也不太会解释,反正就是这么一回事:举例来说,3个节点产生的全连接异构子图只有如图所示的2个,4个点就只有6个。如果你再构建出新的子图形状,那么它一定跟其中某个子图是同构的。
图中标的数字代表根节点可选的位置。例如对于 G 0 G_0 G0,两个节点是等价的(对称的嘛。就,高中化学应该考过这种题吧!),所以只有一种graphlet;对于 G 1 G_1 G1,根节点有在中间和在边上两种选择,上下两个边上的点是等价的,所以只有两种graphlet。其他的类似。节点数为2-5情况下一共能产生如图所示73种graphlet。7
这73个graphlet的核心概念就是不同的形状,不同的位置。
注意这里的graphlet概念和后文图的graphlet kernel的概念不太一样。具体的后文再讲- Graphlet Degree Vector (GDV): Graphlet-base features for nodes
GDV与其他两种描述节点结构的特征的区别: - Degree counts #(edges) that a node touches
- Clustering coefficient counts #(triangles) that a node touches.
- GDV counts #(graphlets) that a node touches
- Graphlet Degree Vector (GDV): A count vector of graphslets rooted at a given node.
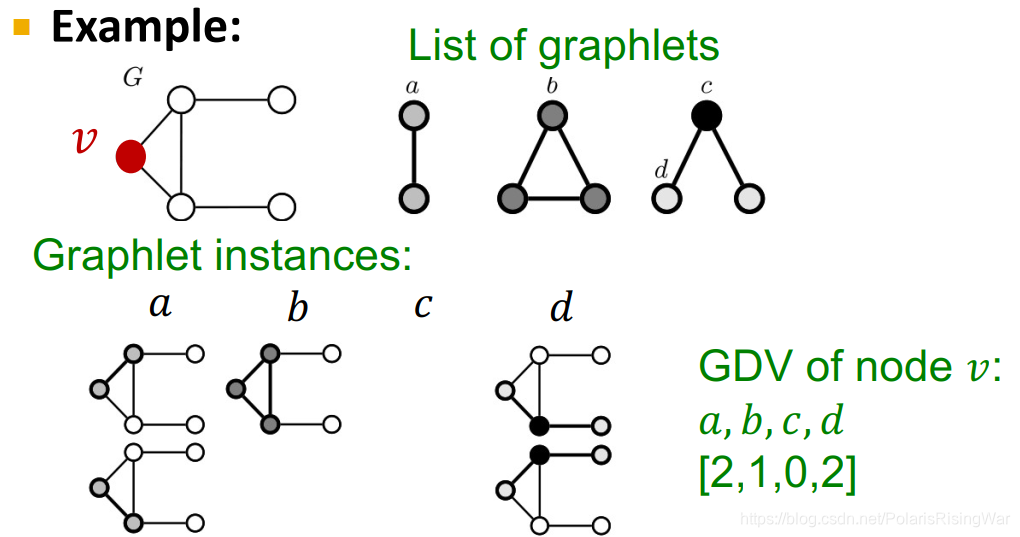 如图所示,对四种graphlet,
v
v
v 的每一种graphlet的数量作为向量的一个元素。
如图所示,对四种graphlet,
v
v
v 的每一种graphlet的数量作为向量的一个元素。
注意:graphlet c的情况不存在,是因为像graphlet b那样中间那条线连上了。这是因为graphlet是induced subgraph5,所以那个边也存在,所以c情况不存在。 - 考虑2-5个节点的graphlets,我们得到一个长度为73个坐标coordinate(就前图所示一共73种graphlet)的向量GDV,描述该点的局部拓扑结构topology of node’s neighborhood,可以捕获距离为4 hops的互联性interconnectivities。
相比节点度数或clustering coefficient,GDV能够描述两个节点之间更详细的节点局部拓扑结构相似性local topological similarity。
- Graphlet Degree Vector (GDV): Graphlet-base features for nodes
- Node Level Feature: Summary
这些特征可以分为两类:- Importance-based features: 捕获节点在图中的重要性

- Structure-based features: 捕获节点附近的拓扑属性
- Importance-based features: 捕获节点在图中的重要性
- Discussion
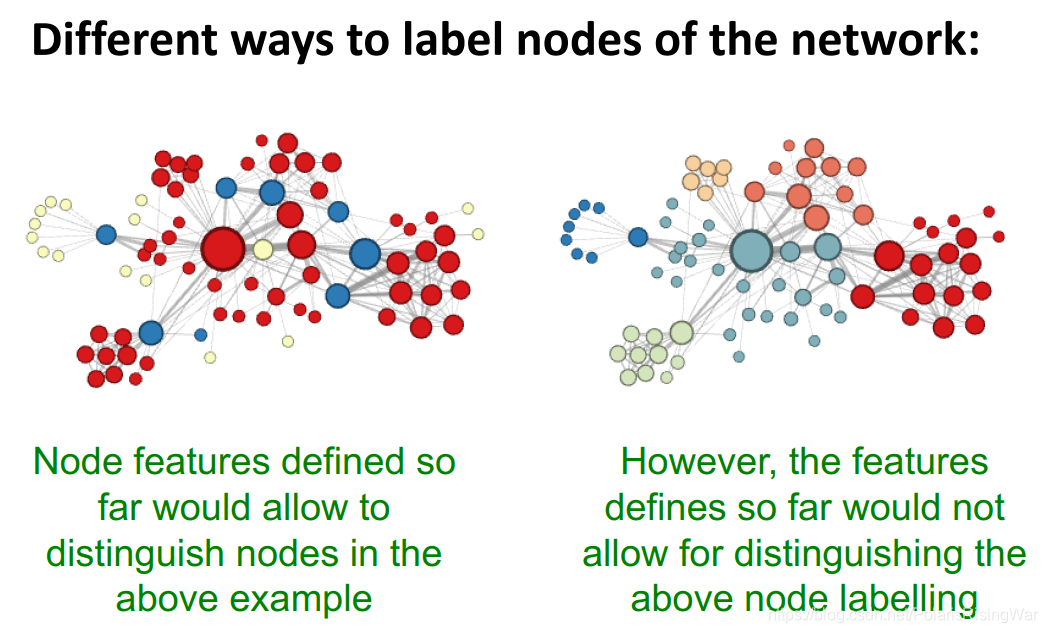 就我的理解,大致来说,传统节点特征只能识别出结构上的相似,不能识别出图上空间、距离上的相似
就我的理解,大致来说,传统节点特征只能识别出结构上的相似,不能识别出图上空间、距离上的相似
3. Traditional Feature-based Methods: Link
- 预测任务是基于已知的边,预测新链接的出现。测试模型时,将每一对无链接的点对进行排序,取存在链接概率最高的K个点对,作为预测结果。
- 特征在点对上
- 有时你也可以直接将两个点的特征合并concatenate起来作为点对的特征,来训练模型。但这样做的缺点就在于失去了点之间关系的信息。
- 链接预测任务的两种类型:随机缺失边;随时间演化边
 图中的 ’ 念prime
图中的 ’ 念prime
第一种假设可以以蛋白质之间的交互作用举例,缺失的是研究者还没有发现的交互作用。(但这个假设其实有问题,因为研究者不是随机发现新链接的,新链接的发现会受到已发现链接的影响。在网络中有些部分被研究得更彻底,有些部分就几乎没有什么了解,不同部分的发现难度不同)
第二种假设可以以社交网络举例,随着时间流转,人们认识更多朋友。 - 基于相似性进行链接预测:计算两点间的相似性得分(如用共同邻居衡量相似性),然后将点对进行排序,得分最高的n组点对就是预测结果,与真实值作比

- distance-based feature:两点间最短路径的长度
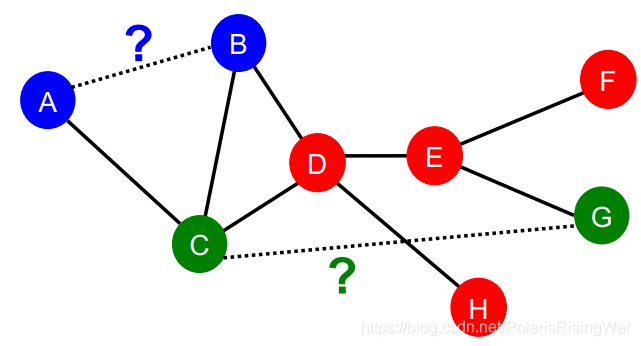
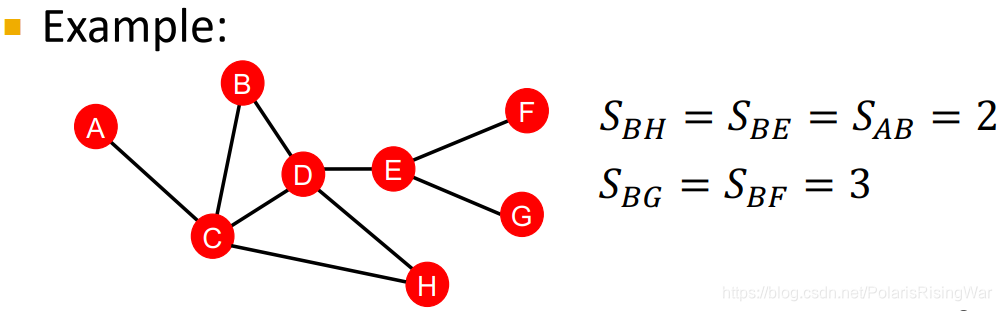 这种方式的问题在于没有考虑两个点邻居的重合度the degree of neighborhood overlap,如B-H有2个共同邻居,B-E和A-B都只有1个共同邻居。
这种方式的问题在于没有考虑两个点邻居的重合度the degree of neighborhood overlap,如B-H有2个共同邻居,B-E和A-B都只有1个共同邻居。 - local neighborhood overlap:捕获节点的共同邻居数
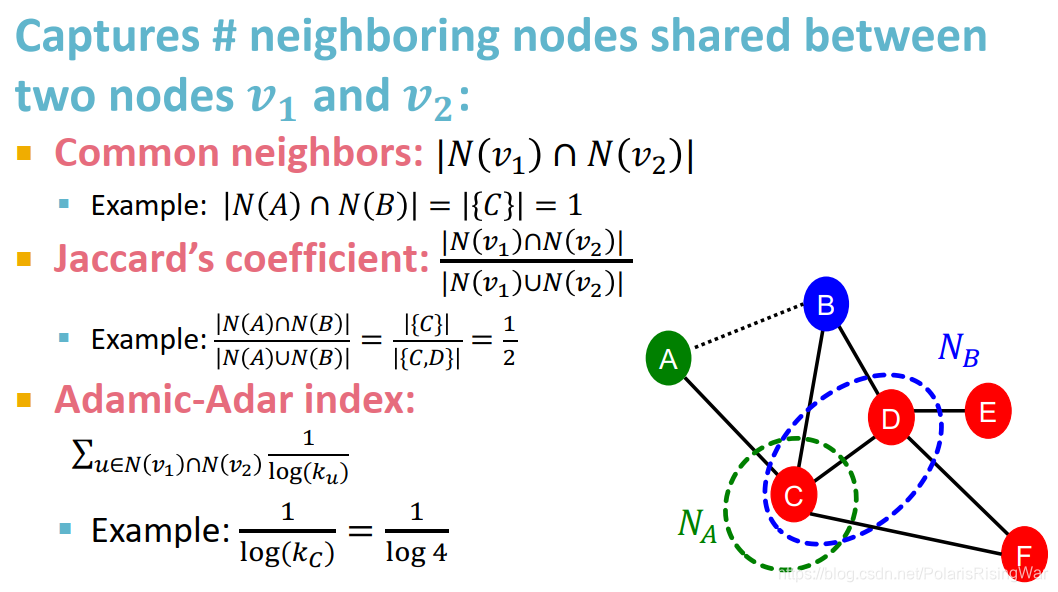 common neighbors的问题在于度数高的点对就会有更高的结果,Jaccard’s coefficient是其归一化后的结果。
common neighbors的问题在于度数高的点对就会有更高的结果,Jaccard’s coefficient是其归一化后的结果。
Adamic-Adar index在实践中表现得好。在社交网络上表现好的原因:有一堆度数低的共同好友比有一堆名人共同好友的得分更高。 - global neighborhood overlap
local neighborhood overlap的限制在于,如果两个点没有共同邻居,值就为0。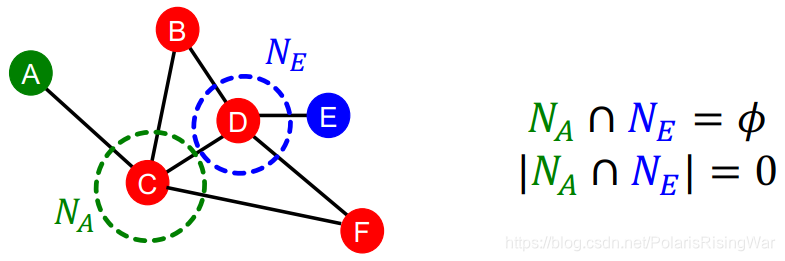
但是这两个点未来仍有可能被连接起来。所以我们使用考虑全图的global neighborhood overlap来解决这一问题。
Katz index:计算点对之间所有长度路径的条数
计算方式:邻接矩阵求幂- 邻接矩阵的k次幂结果,每个元素就是对应点对之间长度为k的路径的条数
- 证明:
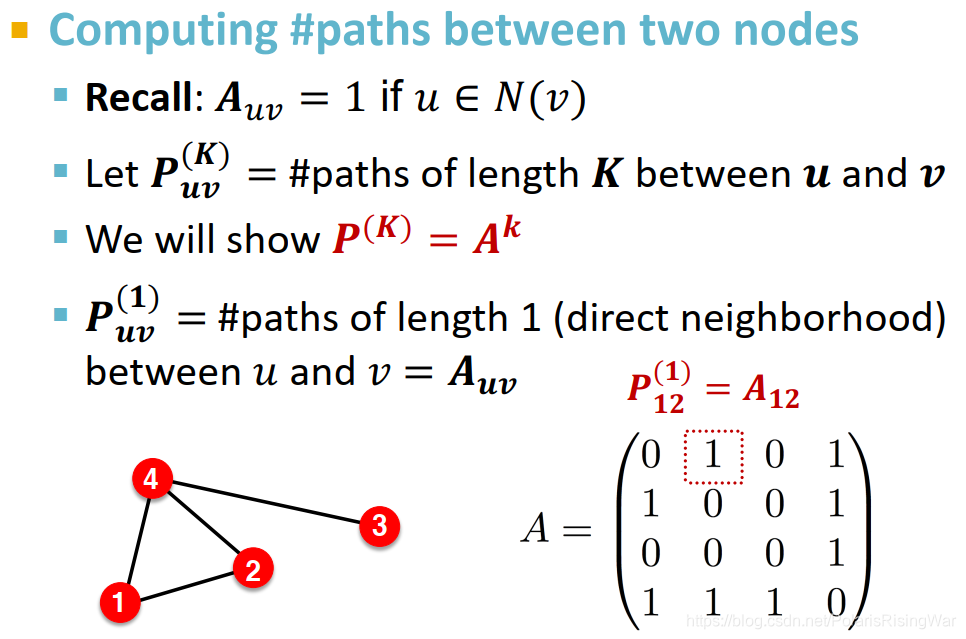 显然
A
u
v
\mathbf{A}_{uv}
Auv代表u和v之间长度为1的路径的数量
显然
A
u
v
\mathbf{A}_{uv}
Auv代表u和v之间长度为1的路径的数量
 计算
u
u
u 和
v
v
v 之间长度为2的路径数量,就是计算每个
u
u
u 的邻居
A
u
i
\mathbf{A}_{ui}
Aui (与
u
u
u 有1条长度为1的路径)与
v
v
v 之间长度为1的路径数量
P
i
v
(
1
)
\mathbf{P}^{(1)}_{iv}
Piv(1) 即
A
i
v
\mathbf{A}_{iv}
Aiv 的总和
∑
i
A
u
i
∗
A
i
v
=
A
u
v
2
\sum_i \mathbf{A}_{ui}*\mathbf{A}_{iv}=\mathbf{A}_{uv}^2
∑iAui∗Aiv=Auv2
计算
u
u
u 和
v
v
v 之间长度为2的路径数量,就是计算每个
u
u
u 的邻居
A
u
i
\mathbf{A}_{ui}
Aui (与
u
u
u 有1条长度为1的路径)与
v
v
v 之间长度为1的路径数量
P
i
v
(
1
)
\mathbf{P}^{(1)}_{iv}
Piv(1) 即
A
i
v
\mathbf{A}_{iv}
Aiv 的总和
∑
i
A
u
i
∗
A
i
v
=
A
u
v
2
\sum_i \mathbf{A}_{ui}*\mathbf{A}_{iv}=\mathbf{A}_{uv}^2
∑iAui∗Aiv=Auv2
同理,更高的幂(更远的距离)就重复过程,继续乘起来 - 从而得到Katz index的计算方式:

 discount factor
β
\beta
β 会给比较长的距离以比较小的权重,exponentially with their length.
discount factor
β
\beta
β 会给比较长的距离以比较小的权重,exponentially with their length.
closed-form闭式解,解析解8
解析解的推导方法我去查了,见尾注9
- Summary
- Distance-based features: Uses the shortest path length between two nodes but does not capture how neighborhood overlaps.
- Local neighborhood overlap:
- Captures how many neighboring nodes are shared by two nodes.
- Becomes zero when no neighbor nodes are shared.
- Global neighborhood overlap:
- Uses global graph structure to score two nodes.
- Katz index counts #paths of all lengths between two nodes.
4. Traditional Feature-based Methods: Graph
- 图级别特征构建目标:找到能够描述全图结构的特征
- Background: Kernel Methods
 就是,核这一部分其实我一直都没搞懂,以前看SVM啥的时候就没好好学都是直接跳的,所以核本来是什么我也不知道……
就是,核这一部分其实我一直都没搞懂,以前看SVM啥的时候就没好好学都是直接跳的,所以核本来是什么我也不知道……
b/w=between
off-the-shelf现成的
不过单纯学习图机器学习的话只要按照图中所说原意来理解应该就行了:两个图的核 K ( G , G ‘ ) K(G,G^`) K(G,G‘) 以标量衡量其相似度,存在特征表示 ϕ ( ⋅ ) \phi (\cdot) ϕ(⋅) 使得 K ( G , G ‘ ) = ϕ ( G ) T ϕ ( G ‘ ) K(G,G^`)=\phi(G)^T\phi(G^`) K(G,G‘)=ϕ(G)Tϕ(G‘)10,定义好核后就可以直接应用核SVM之类的传统机器学习模型。
这个 ϕ \phi ϕ 是个表示向量,可能不需要被显式地计算出来
半正定矩阵特征值非负的证明开我之前写的博文:从0开始的GNN导学课程笔记 - Overview

- graph kernel: key idea
 bag-of-words相当于是把文档表示成一个向量,每个元素代表对应word出现的次数。
bag-of-words相当于是把文档表示成一个向量,每个元素代表对应word出现的次数。
此处讲述的特征抽取方法也将是bag-of-something的形式,将图表示成一个向量,每个元素代表对应something出现的次数(这个something可以是node, degree, graphlet, color)
光用node不够的话,可以设置一个degree kernel,用bag-of-degrees来描述图特征
- graphlet features
- Key idea: Count the number of different graphlets in a graph.
- 注意这里对graphlet的定义跟上文节点层面特征抽取里的graphlet不一样。区别在于:
- Nodes in graphlets here do not need to be connected (allows for isolated nodes)
- The graphlets here are not rooted.
- 对每一种节点数,可选的graphlet:
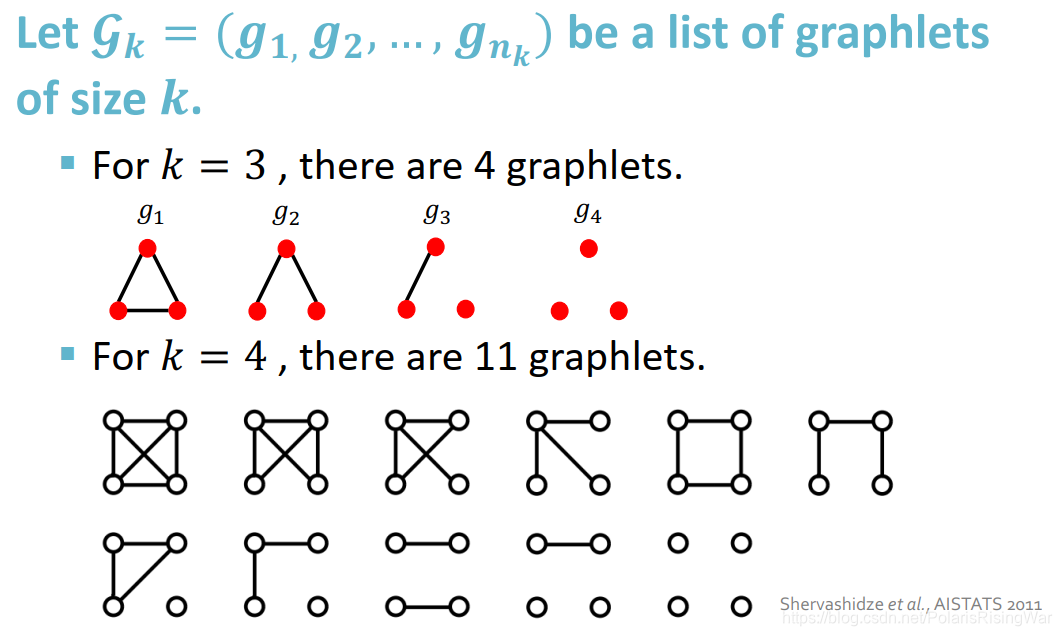
- graphlet count vector:每个元素是图中对应graphlet的数量
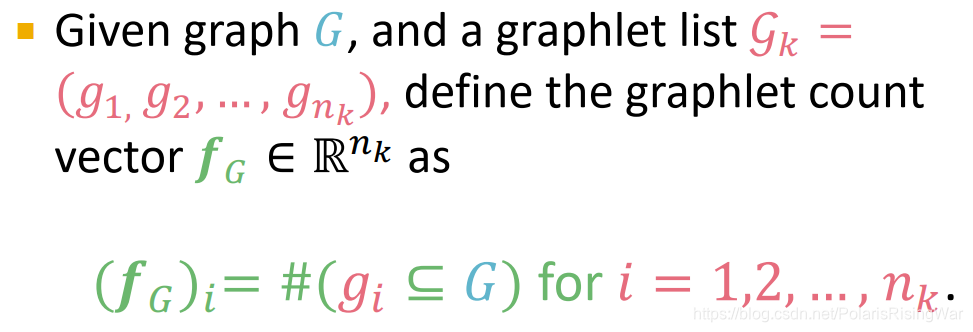
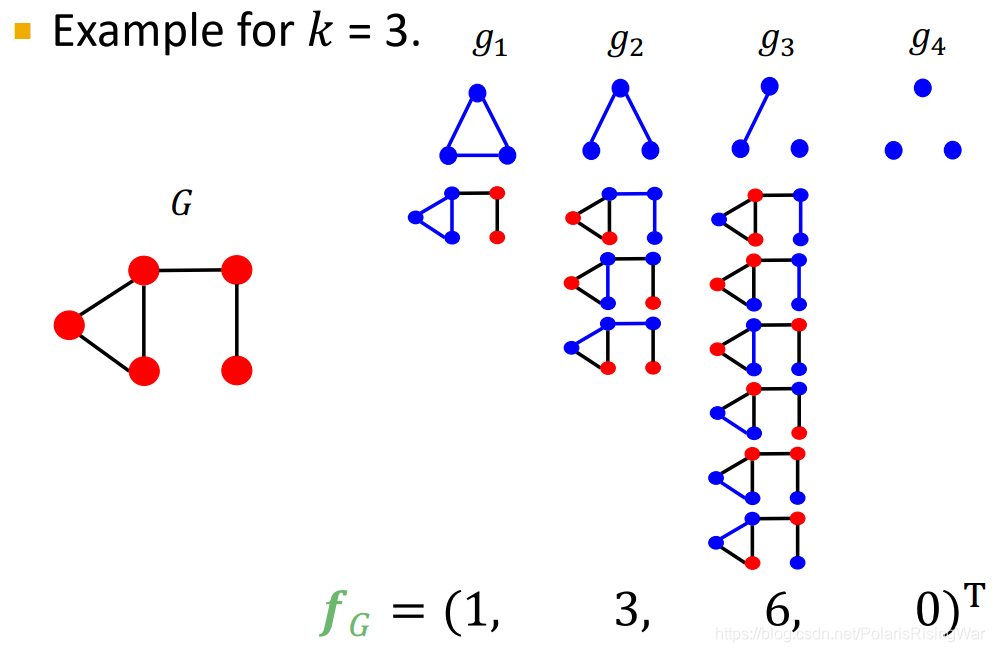
- graphlet kernel就是直接点积两个图的graphlet count vector得到相似性。对于图尺寸相差较大的情况需进行归一化
 skew扭曲
skew扭曲
h捕获了图中我们要的graphlet的frequency或proportion - graphlet kernel的限制:计算昂贵(这一部分的知识对我来说超纲了,我就只知道有这么回事就完了,我来不及学为啥了)

- Weisfeiler-Lehman Kernel:相比graphlet kernel代价较小,效率更高。
用节点邻居结构迭代地来扩充节点信息(vocabulary在此仅作引申义?)

- 实现算法:Weisfeiler-Lehman graph isomorphism test=color refinement11
 c
v
(
k
)
c^{(k)}_v
cv(k) 念成c capital k of v
c
v
(
k
)
c^{(k)}_v
cv(k) 念成c capital k of v - color refinement示例
把邻居颜色聚集起来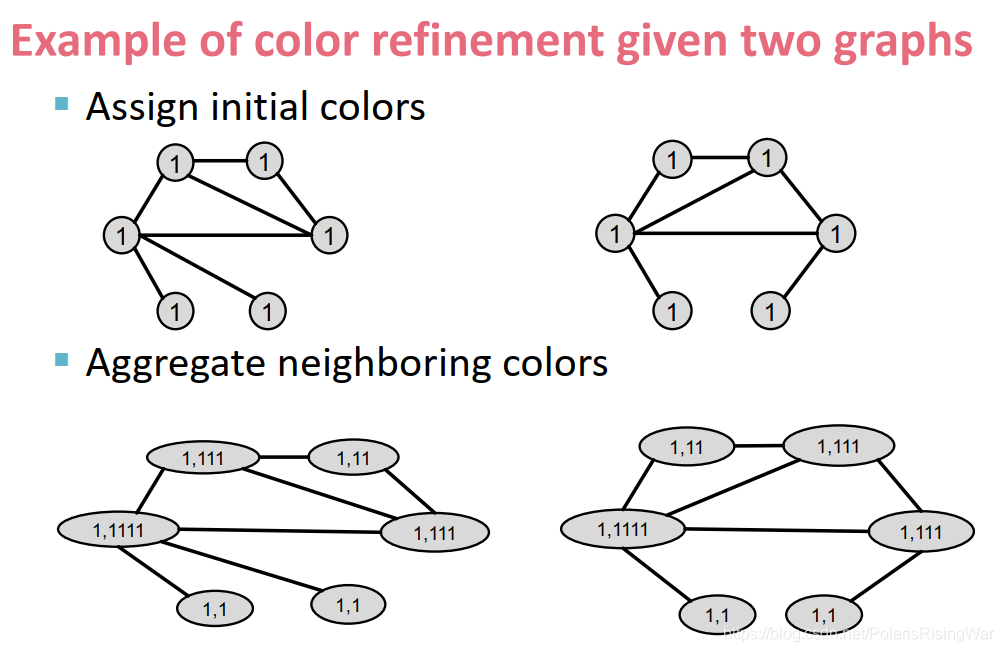
对聚集后颜色取哈希值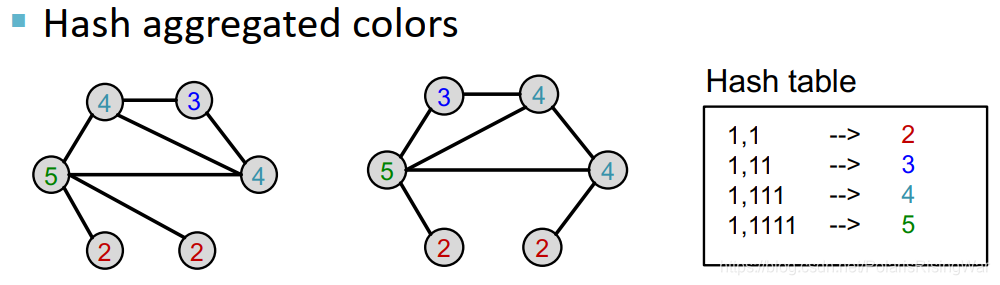
把邻居颜色聚集起来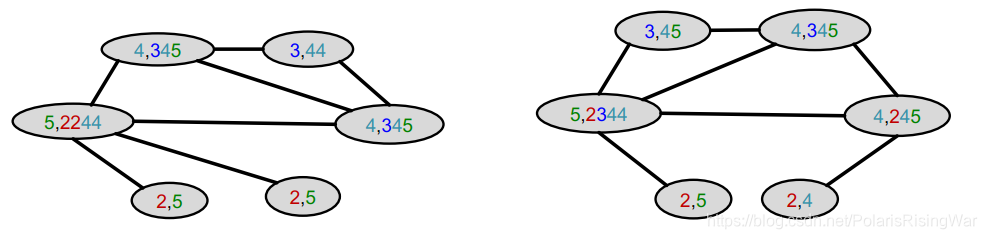
对聚集后颜色取哈希值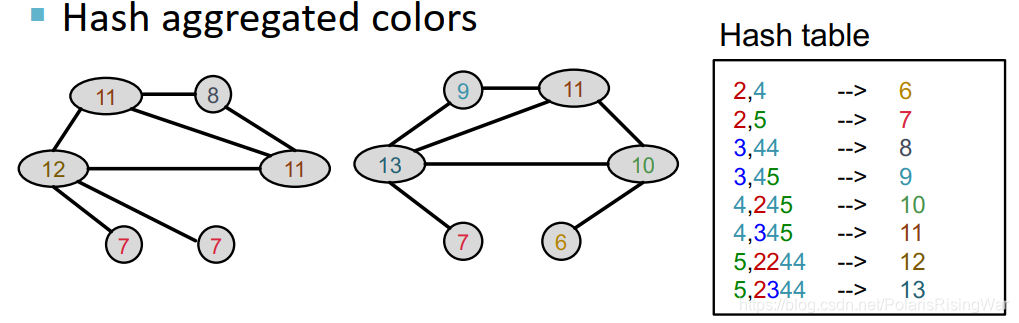
- 进行K次迭代12后,用整个迭代过程中颜色出现的次数作为Weisfeiler-Lehman graph feature
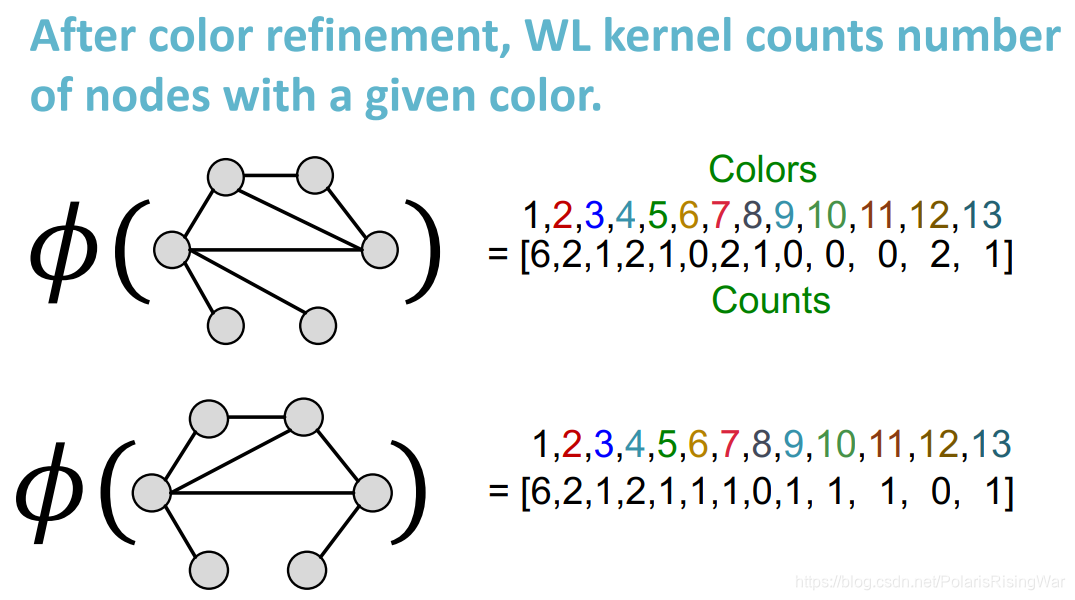 第一个图的特征应该是算错了,最后3个元素应该是2 1 0
第一个图的特征应该是算错了,最后3个元素应该是2 1 0 - 用上图的向量点积计算相似性,得到WL kernel
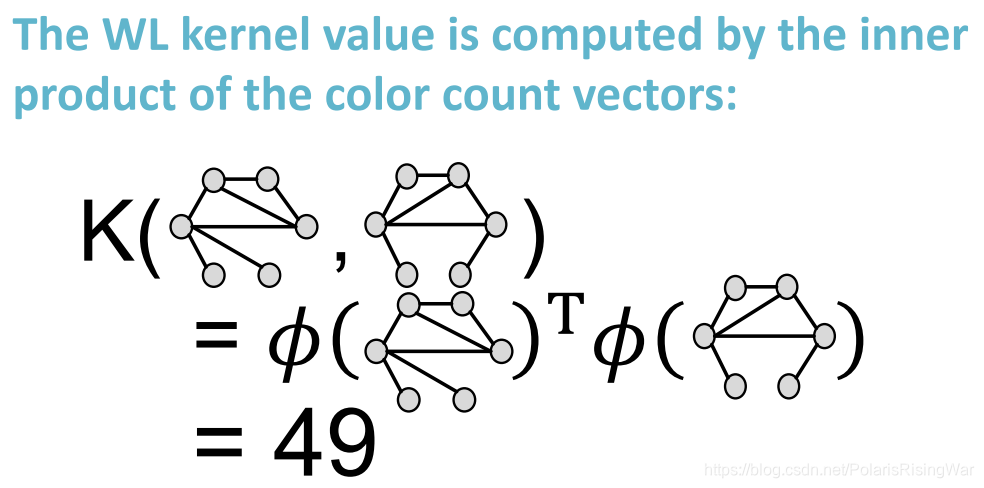
- WL kernel的优势在于计算成本低
 w.r.t: with respect to
w.r.t: with respect to
颜色个数最多是节点的个数:每一次就最多这么多个点上有颜色……
- 实现算法:Weisfeiler-Lehman graph isomorphism test=color refinement11
- Summary
 这个color refinement方法与GNN的相似性我认为有二,一在都聚集了节点邻居信息13,GNN详情见我撰写的后续课程笔记(就后面好几节课都讲了GNN);二在在Lecture 9中会讲的GIN14。
这个color refinement方法与GNN的相似性我认为有二,一在都聚集了节点邻居信息13,GNN详情见我撰写的后续课程笔记(就后面好几节课都讲了GNN);二在在Lecture 9中会讲的GIN14。
5. 本章总结
- Traditional ML Pipeline
- Hand-crafted feature + ML model
- Hand-crafted features for graph data
- Node-level:
- Node degree, centrality, clustering coefficient, graphlets
- Link-level:
- Distance-based feature
- local/global neighborhood overlap
- Graph-level:
- Graphlet kernel, WL kernel
- Node-level:
因为感觉一般attribute和property都翻译成特征,所以有点迷惑他们有什么区别,简单看了一下ResearchGate问题:What are the differences between attribute and properties ?
最高赞回答:区别微妙,attribute是对物体的附加属性,property是体现物体本身特征的属性。一般来说,是同义词。 ↩︎谷歌了一下,发现这个定理挺难的,没看懂。
……数学太难为我了,我放弃了。 ↩︎对聚集系数进行解释的其他参考资料:
聚集系数 - 百度百科
Clustering coefficient(集聚系数)
我还没有仔细学习具体定义。仅供参考。 ↩︎参考资料:
① 知乎问题:很多地方的组合数记法为什么要用两个圆括号包起来而不是用原来的C下标上标?
② 知乎问题: 如何通俗的解释排列公式和组合公式的含义?
③ 百度知道问答:排列组合中A和C怎么算啊 ↩︎subgraph, induced subgraph等概念可参考cs224w课程第12章Frequent Subgraph Mining with GNNs。我以后也会写相应的笔记 ↩︎ ↩︎
对connected的定义可以参考我之前写的cs224w第一章笔记,里面有写:cs224w(图机器学习)2021冬季课程学习笔记1 ↩︎ ↩︎
对这部分的讲解参考了这篇博文:【图神经网络】——“斯坦福CS224W”课程笔记(三)
这篇博文做的是19版课程的笔记,主要讲的是motif和graphlet相关概念。这些概念在21版课程中会放到后面讲(还是在第12章的位置),后面我也会做到相应的笔记。 ↩︎参考知乎问题:什么叫闭型(closed-form)? ↩︎
β \beta β 是权重衰减因子,为了保证数列的收敛性,其取值需小于邻接矩阵A最大特征值的倒数。(具体原因见参考资料⑤)
该方法权重衰减因子的最优值只能通过大量的实验验证获得,因此具有一定的局限性。
解析解推导过程:
矩阵形式的表达式为 S = β A + β 2 A 2 + β 3 A 3 … S=\beta A+\beta ^{2}A^{2}+\beta ^{3}A^{3}\ldots S=βA+β2A2+β3A3…
( I − β A ) ( I + S ) = ( I − β A ) ( I + β A + β 2 A 2 + β 3 A 3 … ) = ( I + β A + β 2 A 2 + β 3 A 3 … ) − ( β A + β 2 A 2 + β 3 A 3 … ) = I \begin{aligned} & (I-\beta A)(I+S) \\ =& (I-\beta A)(I+\beta A+\beta ^{2}A^{2}+\beta ^{3}A^{3}\ldots) \\ =& (I+\beta A+\beta ^{2}A^{2}+\beta ^{3}A^{3}\ldots)-(\beta A+\beta ^{2}A^{2}+\beta ^{3}A^{3}\ldots) \\ =& I \end{aligned} ===(I−βA)(I+S)(I−βA)(I+βA+β2A2+β3A3…)(I+βA+β2A2+β3A3…)−(βA+β2A2+β3A3…)I
所以 I + S = ( I − β A ) − 1 I+S=(I-\beta A)^{-1} I+S=(I−βA)−1
故 S = ( I − β A ) − 1 − I S=(I-\beta A)^{-1}-I S=(I−βA)−1−I
参考资料:
①Katz 指标(The Katz Index,KI)的讲解与详细推导
②刘建国, 任卓明, 郭强,等. 复杂网络中节点重要性排序的研究进展[J]. 物理学报, 2013(17):9-18. 论文下载地址
③维基百科:Katz centrality 就是,这个Katz centrality就是Katz index的一个求和。所以如果需要的话也可以查看Katz centrality的相关资料。但我没看毕竟我不想看
④Katz, L. (1953). A new status index derived from sociometric analysis. Psychometrika, 18(1), 39–43. 论文下载地址 据我观察这个应该是原始论文了。但我没看毕竟我不想看
⑤Junker B H, Schreiber F. Analysis of biological networks[M]. John Wiley & Sons, 2011. 谷歌学术提供的书籍下载地址 据我观察,这本书里应该有讲为什么 β \beta β 需小于邻接矩阵A最大特征值的倒数……但这TM是一本书(358页!)我怎么可能看,我安详地死了。
⑥Martinez V , Berzal F , Cubero J C . A Survey of Link Prediction in Complex Networks[J]. Acm Computing Surveys, 2017, 49(4):69.1-69.33. 论文下载地址 一篇链接预测的综述。但我没看毕竟我不想看 ↩︎说来无用,但是我觉得这个表示形式很像图数据在谱域上的卷积。
……但是这就像洛伦兹力的形式很像万有引力定律的公式,感觉我看到了也没什么用。 ↩︎我一开始疑惑了一下那个 c ( 0 ) ( v ) c^{(0)}(v) c(0)(v) 对每个点的初始赋值是不是一样的,因为在这里没有说,但是在后面的例子中显示是一样的。然后我查了一下,在这篇文档:Color Refinement and its Applications 里看到它的算法第一步直接写成这样:
 虽然这篇文档别的内容我都没看,但是我觉得据此看来初始赋值应该是都一样的。
虽然这篇文档别的内容我都没看,但是我觉得据此看来初始赋值应该是都一样的。
(2021.6.29补:我看了Lecture9的视频,说这个颜色也可以按照节点度数之类的来分配。估计可以随便分,问题不大) ↩︎color refinement的结束条件是设置迭代次数还是达到收敛我有点没搞懂,但是这玩意真的能收敛到稳定状态吗?看起来不行啊! ↩︎
关于这个GNN空间方法为什么是聚集邻居信息啊,我主要看到过两种说法,一种是它反正就是这么干的,这么干本来就很符合直觉嘛(马克思说过,人是社会性的动物,节点受其邻居影响是很直觉的嘛,就像KNN一样);另一种是其做法发源自其他方法,一说是来源于谱方法(但是具体怎么来的我没搞懂,反正就是好像经过一番推导可以从谱方法简化到空间方法),一说是受belief propagation启发,一说是受CNN启发。
真是太复杂了,我搞不懂。 ↩︎可参考我撰写的博文:cs224w(图机器学习)2021冬季课程学习笔记11 Theory of Graph Neural Networks ↩︎





 本文介绍了传统图机器学习中针对节点、链接和图级别的特征设计,包括节点度、中心性、簇密度、图灵子结构(如GDV)以及链接预测的度量方法(如距离、邻接度重叠和Katz指数)。重点讨论了手工艺特征结合机器学习模型的传统流程。
本文介绍了传统图机器学习中针对节点、链接和图级别的特征设计,包括节点度、中心性、簇密度、图灵子结构(如GDV)以及链接预测的度量方法(如距离、邻接度重叠和Katz指数)。重点讨论了手工艺特征结合机器学习模型的传统流程。

















 1361
1361












