【工程应用十二】Bayer图像格式中Hamilton-Adams及Zhang Wu 基于LMMSE算法的Demosaic过程优化。...-优快云博客

　　Demosaic，中文直接发翻译为去马赛克，但是其本质上并不是去除马赛克，这让很多第一次接触这个名词或者概念的人总会想的更多。因此，一般传感器在采集信息时一个位置只采集RGB颜色中的一个通道，这样可以减少采集量，降低成本，由于人的视觉对绿色最为敏感，所以一般情况下，绿色分量会比红色和蓝色分量多一倍的信息，这样，根据RGB不同的位置排布，就产生了RGGB、GBRG、GRBG、BGGR四种常用的模式，比如RGGB模式就如下所示：

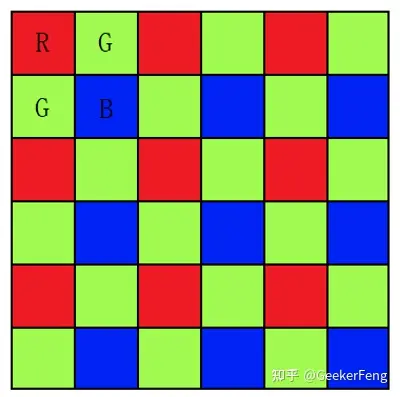
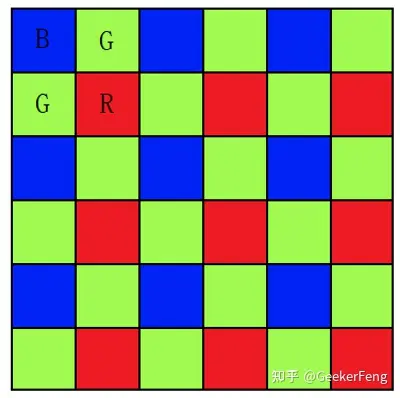
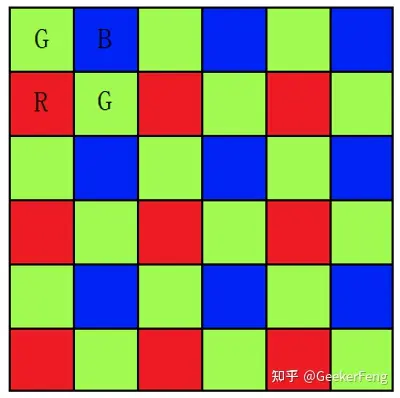
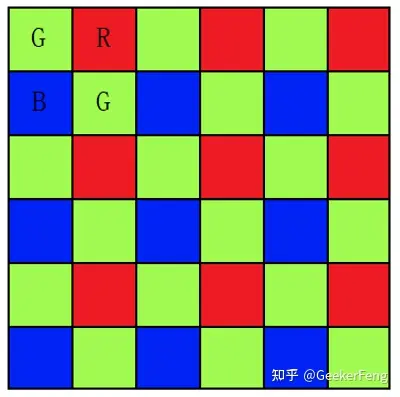
　　　　RGGB　　　　　　　　　　　　BGGR　　　　　　　　　　　　GBRG　　　　　　　　　　　　　GRBG

　　去马赛克的目的就是从这些确实的信息中尽量的完美的复原原始信息，比如上图第一个点，只有红色分量是准确的，那就要想办法通过其他的信息重构出改点的绿色和蓝色分量。

　　目前，关于这方面的资料也是很多的，这里我描述下目前我已经优化和处理的四个算法，并分享部分代码。

　　一、双线性处理

　　一个最为直接和简单的想法就是利用领域的相关信息通过插值来弥补当前缺失的颜色分量，我们以RGGB格式为例，参考上图(坐标都是从0开始，X轴从左向右递增，Y轴从上向下递增)。

　　先不考虑边缘。

　　比如(1,1)坐标这个点，现在已经有了B这个分量，缺少R和G这个分量，但是他四个对角线上都有R分量，因此，可以使用这个4个像素的平均值来计算改点的R分量，而在其上下左右四个方向有恰好有4个点的G分量，同理可以用这个四个的平均值来评估当前点的G值。

　　在考虑(1,2)这个坐标点，他的当前有效值是G分量，缺少R和B分量，而他则没有(1,1)点那么幸运，他周边的有效R和B分量都只有2个，因此，只能利用这两个有效值的平均值来评估该点的R/B分量。

　　其他的点类似处理。

　　在考虑边缘，由于边缘处的像素总有某一个方向或某二个方向缺少像素，因此，可以利用镜像的关系把缺少的那一边取镜像的位置信息来补充。

　　一个简单的高效的C++代码如下所示：

int IM_DecodeBayerRG8ToBGR_Bilinear_PureC(unsigned char* Src, BitmapData Dest)
{
    int Status = IM_STATUS_OK;
    int Width = Dest.Width, Height = Dest.Height, Stride = Dest.Stride;
    if (((Width & 1) == 1) || ((Height & 1) == 1))    return IM_STATUS_INVALIDPARAMETER;
    if ((Width < 8) || (Height < 8))                return IM_STATUS_INVALIDPARAMETER;
    unsigned char* RowCopy = (unsigned char*)malloc((Width + 2) * 3 * sizeof(unsigned char));
    if (RowCopy == NULL)    return IM_STATUS_OUTOFMEMORY;
    unsigned char* First = RowCopy;
    unsigned char* Second = RowCopy + (Width + 2);
    unsigned char* Third = RowCopy + (Width + 2) * 2;
    unsigned char* SrcP = (unsigned char*)Src;
    Second[0] = SrcP[0];
    memcpy(Second + 1, SrcP, Width * sizeof(unsigned char));
    Second[Width + 1] = SrcP[Width - 1];
    memcpy(First, Second, (Width + 2) * sizeof(unsigned char));            //    第一行和第二行一样
    Third[0] = SrcP[Width];
    memcpy(Third + 1, SrcP + Width, Width * sizeof(unsigned char));
    Third[Width + 1] = SrcP[Width + Width - 1];
    for (int Y = 0; Y < Height; Y++)
    {
        unsigned char* LinePD = Dest.Scan0 + Y * Stride;
        if (Y != 0)
        {
            unsigned char* Temp = First; First = Second; Second = Third; Third = Temp;
        }
        if (Y == Height - 1)
        {
            memcpy(Third, Second, (Width + 2) * sizeof(unsigned char));
        }
        else
        {
            Third[0] = SrcP[(Y + 1) * Width];
            memcpy(Third + 1, SrcP + (Y + 1) * Width, Width * sizeof(unsigned char));
            Third[Width + 1] = SrcP[(Y + 1) * Width + Width - 1];
        }
        if ((Y & 1) == 0)        //    偶数列
        {
            for (int X = 0; X < Width; X++, LinePD += 3)
            {
                int P0 = First[X], P1 = First[X + 1], P2 = First[X + 2];
                int P3 = Second[X], P4 = Second[X + 1], P5 = Second[X + 2];
                int P6 = Third[X], P7 = Third[X + 1], P8 = Third[X + 2];
                if ((X & 1) == 0)
                {
                    LinePD[0] = (P0 + P2 + P6 + P8 + 2) >> 2;
                    LinePD[1] = (P1 + P3 + P5 + P7 + 2) >> 2;
                    LinePD[2] = P4;
                }
                else
                {
                    LinePD[0] = (P1 + P7 + 1) >> 1;
                    LinePD[1] = P4;
                    LinePD[2] = (P3 + P5 + 1) >> 1;
                }
            }
        }
        else
        {
            for (int X = 0; X < Width; X++, LinePD += 3)
            {
                int P0 = First[X], P1 = First[X + 1], P2 = First[X + 2];
                int P3 = Second[X], P4 = Second[X + 1], P5 = Second[X + 2];
                int P6 = Third[X], P7 = Third[X + 1], P8 = Third[X + 2];
                if ((X & 1) == 0)
                {
                    LinePD[0] = (P3 + P5 + 1) >> 1;
                    LinePD[1] = P4;
                    LinePD[2] = (P1 + P7 + 1) >> 1;
                }
                else
                {
                    LinePD[0] = P4;
                    LinePD[1] = (P1 + P3 + P5 + P7 + 2) >> 2;
                    LinePD[2] = (P0 + P2 + P6 + P8 + 2) >> 2;
                }
            }
        }
    }
    free(RowCopy);
    return IM_STATUS_OK;
}

　　这个算法是非常高效的，而且极易使用指令集优化，在一台普通的配置的PC上(12th Gen Intel(R) Core(TM) i7-12700F 2.10 GHz)处理1902*1080的图，大概只需要2ms，SSE优化后可以做到0.6ms，但是这个方法忽略边缘结构和通道间的相关性，从而容易导致颜色伪彩和图像模糊，比如下面这个经典的测试图，解码后的结果有点惨不忍睹。　