数据结构-堆（java实现）

原创已于 2023-11-14 08:10:56 修改 · 616 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

于 2019-02-05 05:32:15 首次发布

算法与数据结构专栏收录该内容

5 篇文章

订阅专栏

本文深入讲解了堆数据结构的概念，包括小堆和大堆的定义，堆的性质以及堆的创建和调整的时间复杂度。同时，通过Java代码示例展示了如何使用优先级队列来实现堆。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

概念

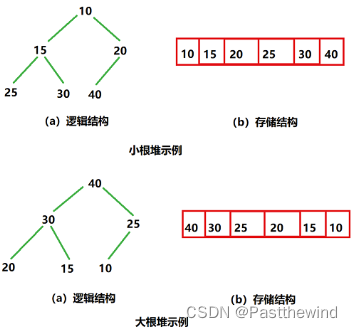
如果有一个关键码的集合 K = {k0 ， k1 ， k2 ， … ， kn-1} ，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足： Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >=K2i+2) i = 0 ， 1 ， 2… ，则称为小堆 ( 或大堆) 。

（即双亲比孩子的数值小(大)——小(大)堆）将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

性质

堆中某个节点的值总是不大于或不小于其父节点的值
堆总是一棵完全二叉树

可以看下可视化操作，对堆数据结构加深理解：二叉堆（优先队列） - VisuAlgo

创建堆：O(N)

调整堆：O(log2N)

实现堆

实现堆可以借助优先级队列，首先看一下Java中优先级队列的API，直接上代码：

public class Heap {
    public static void main(String[] args) {
        // 小根堆
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        // 大根堆
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2-o1;
            }
        });
        System.out.println("大根堆");
        System.out.println("入堆");
        maxHeap.add(3);
        maxHeap.add(1);
        maxHeap.add(2);
        maxHeap.add(4);
        System.out.println("3-1-2-4已入大根堆");
        System.out.println("大根堆-堆顶元素：" + maxHeap.peek()); // 4

    }
}