【典中典】八皇后问题之C语言解法（重制版）

具体历史背景我记不清了，但其核心就是皇后的摆放问题。具体来说，就是在一个4*4的正方形格子棋盘中，（具体参考国际象棋），需要在棋盘中摆放最多的皇后，使她们不能互相攻击即可。（看上去简单吧！从这些信息来看，我们可以很轻松的理解到，在这个正方形的棋盘中，每一行只可以放置一个皇后；同理，每一列也只能放置一个皇后。如果真是这样，问题就会立刻变得非常简单：在n*n的棋盘中，最多、且只能放置n个皇后，皇后的摆放数目就是A(n,n)，即1*2*3*....*n。然而，事情并没有这么简单。）

二、重点难点

1.问题的综合论述与分析

在这个问题中，我认为重难点也可以混为一谈。

皇后不能相互攻击的条件是什么？就是皇后们不能站在彼此的两条斜对角线上！如图

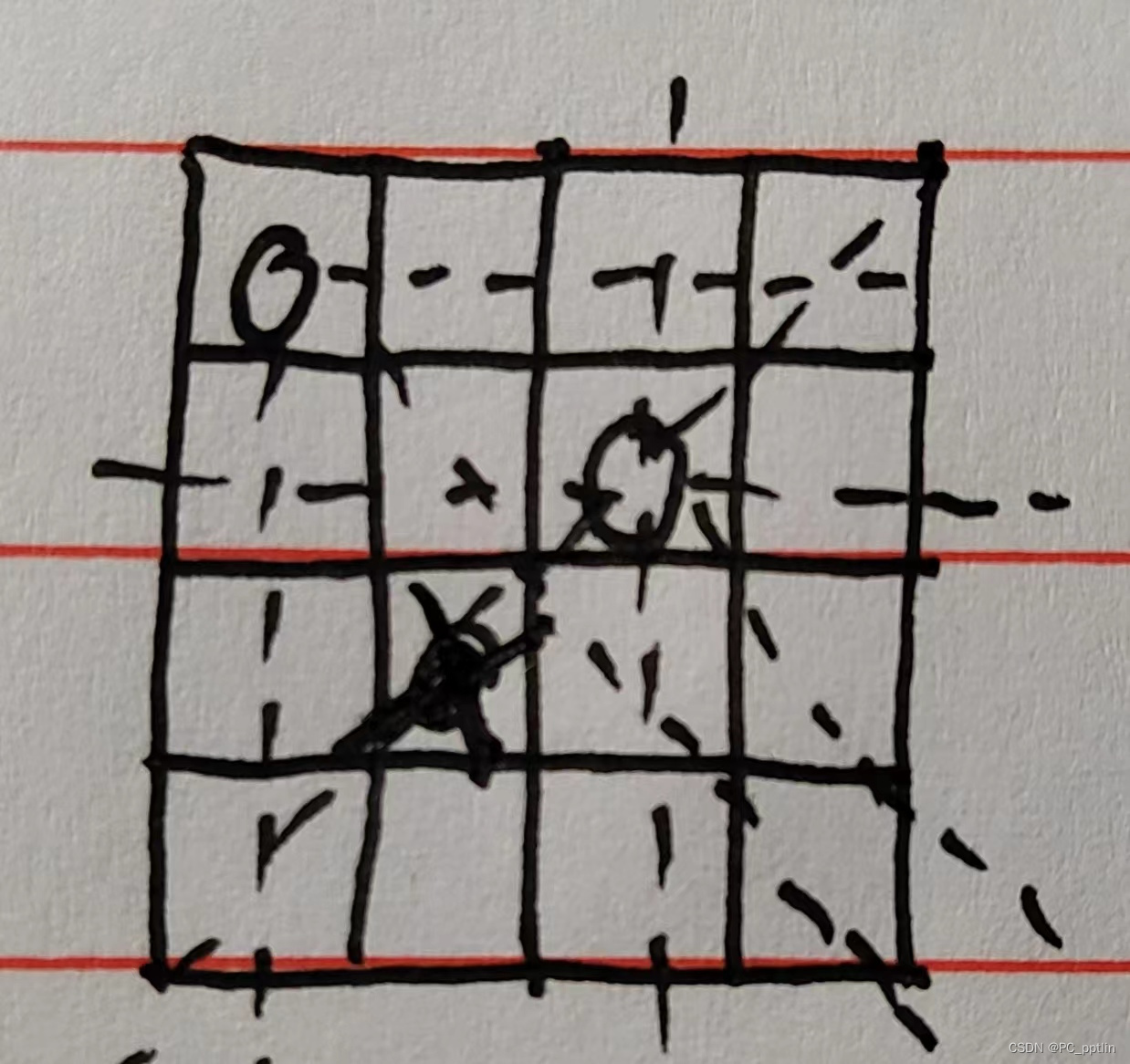
这就需要我们抽象出自己的思维了---->能否设计出来一个函数1，这个函数的主要功能是一步一步的放置皇后，然后再编写一个函数2，这个函数2负责接收函数1所创造出的棋盘的皇后摆放状态，判断这个点（位置）究竟可不可以放置皇后呢？如果这个位置可以放置皇后，则函数2返回ture，告知函数1该位置可以放置，函数1跳转至第二行从第一个位置开始放置；若不可以，则跳过该行的这个位置，把下一个位置和棋盘信息传给函数2进行判断。但是问题又出来了：如果在某一行中所有位置都试过一遍了，就像图片中的第三行一样，这四个位置都不可以放置，难道程序就要停止吗？很显然，档当然不行，因为我们还没有找到一个解法。但是我们发现，在第二行中，貌似还有第四个位置没有得到尝试。于是我们需要回退，然后再从第三行的第一个位置开始找起。那么，难点来了：像这样的带有遍历、回退、并且可以保留之前

不冲突皇后摆法的程序，应该怎么设计呢？幸运的是，这种情况，如果利用递归的话，程序设计的妥当，因该是可以解决八皇后问题的。但是，怎么递归？带有递归的函数应该怎么设计？这些是值得思考的问题。

2.程序设计的具体分析

先看函数2吧，因为函数2比较简单（滑稽）函数1负责将它想要判断的是否可行的位置传给函数2判断，而函数2只需要看看这个位置的米字型放射线路中有没有放置其他皇后即可。判断完毕直接返回status状态值即可。

接下来看看函数1吧。递归的函数，其自身应该也需要带有递归的性质。所谓回退，是否可以看成是当前进程的最后一步（就是最后一次递归的函数）消亡，然后返回上一级函数在进行循环呢？上一级函数的对皇后放置的位置的循环还没有结束，就像之前描述的，还有跟多的位置可以尝试。于是我们得出结论：函数递归调用自身应该在一个循环当中，并且还得是在函数1在对当前的棋盘的摆放位置改变了之后进行调用。这样的话，再每次调用函数的时候，之前的状态便会被更新上去。说白了，每一次皇后问题摆法的解出，都是函数的调用（在不失败，即没有回退的情况下）累计了七次的结果。我们可以在函数中传入row这个变量，每次递归之后就row++，row变成8的时候就说明已经排满了，可以输出第一个皇后问题的解法了。如果这些话语让你觉得有些啰嗦，请见谅，这毕竟是我第一次写博客，也请往后看。总之，我们看出整个问题的求法就是不断地、一行一行的向后找摆法即可。

3.需要具备的C语言基础

这里笔者使用的是C语言中的malloc函数来定义数组指针，本质上是个指针，这样直接在堆中开辟内存内存空间，不过你要是不想用的话应该也不是不行。具体如下，要注意使用函数时对malloc的类型转换要与数组指针的类型吻合。

int (*chess)[n] = (int(*)[n]) malloc(n * n * sizeof(int));

三、代码与解释

1.前奏

好了，说了这么多，咱们直接来看完整的代码：

#include <stdio.h>
#include <stdlib.h>

int notEqual(int row, int j, int n, int (*chess)[n]){//落子判断算法(函数)
	int i, k, flag1=0,flag2=0,flag3=0,flag4=0,flag5=0;
	for(i=0;i<n;i++)
		if (*(*(chess + i) + j) != 0){
			flag1 = 1;
			break;
		}
	for (i=row,k=j;i>=0&&k>=0;i--,k--)
		if (*(*(chess + i) + k) != 0){
			flag2 = 1;
			break;
		}
	for (i=row,k=j;i<n&&k<n;i++,k++)
		if (*(*(chess + i) + k) != 0){
			flag3 = 1;
			break;
		}
	for (i=row,k=j;i>=0&&k<n;i--,k++)
		if (*(*(chess + i) + k) != 0){
			flag4 = 1;
			break;
		}
	for (i=row,k=j;i<n&&k>=0;i++,k--)
		if (*(*(chess + i) + k) != 0){
			flag5 = 1;
			break;
		}
	if (flag1==1 || flag2==1 || flag3==1 || flag4==1 || flag5==1)
		return 0;
	else return 1;
}
void eightQueen(int row, int n, int (*chess)[n], int *count){
	int i, j, k, t;
	int chess2[n][n];
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			chess2[i][j] = *(*(chess+i)+j);
	if(row==n){
		printf("Solution %d:\n",(*count)++);
		for(k=0;k<n;k++){
			for(t=0;t<n;t++)
			    printf("%d ",*(*(chess2+k)+t));
			printf("\n");
		}
		printf("\n");
	}//瞻前顾后
	else{
		for(j=0;j<n;j++){// 0 0 8 原始棋盘
			if(notEqual(row,j,n,chess)){
				for(i=0;i<n;i++)
					*(*(chess2 + row) + i) = 0; 
				*(*(chess2 + row) + j) = 1;
				eightQueen(row+1, n, chess2, count);
			}
		}
	}
}

int main(){
	int n;
	scanf("%d",&n);
	int (*chess)[n]=(int(*)[n])malloc(n * n * sizeof(int));
	if(chess == NULL){
		printf("Memory allocation failed.\n");
		return -1;
	}
	int count = 1;
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			chess[i][j] = 0;
		}
	}
	eightQueen(0, n, chess, &count);
	printf("The number of solutions for %d-queen is %d\n", n, count-1);
	free(chess);
	return 0;
}

很长吧？哈哈，其实也就是看起来很长，主函数main()与与条件判断函数notEqual()函数十分易于理解。主函数只需负责开出n*n二维数组（其实就是数组指针，指向数组的指针，只不过指针指向的东西有了实际的空间），然后赋初始值均为0在调用函数eightQueen()即可；而notEqual()函数其实就是判断当前给它传进去的位置合不合法而已，只是你需要进行五次循环判断---->米字型的两条对角线*2就是4，再加上一竖列即可。

2.重头戏

接下来的eightQueen函数才时难理解并且最关键的函数。我们来纵观一下它：

void eightQueen(int row, int n, int (*chess)[n], int *count){
	int i, j, k, t;
	int chess2[n][n];
	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			chess2[i][j] = *(*(chess+i)+j);
	if(row==n){
		printf("Solution %d:\n",(*count)++);
		for(k=0;k<n;k++){
			for(t=0;t<n;t++)
			    printf("%d ",*(*(chess2+k)+t));
			printf("\n");
		}
		printf("\n");
	}
	else{
		for(j=0;j<n;j++){
			if(notEqual(row,j,n,chess)){
				for(i=0;i<n;i++)
					*(*(chess2 + row) + i) = 0; 
				*(*(chess2 + row) + j) = 1;
				eightQueen(row+1, n, chess2, count);
			}
		}
	}
}

你会发现，这个函数其实也就这几个功能：变量row进行传入，初始化为0，之后每次递归都要加1，达到向下找皇后摆法的目的。当最后一次递归调用后，函数发现row已经变成8，说明皇后已经摆满，如此，就把这种解法打印出来，然后函数消亡，回到上一级函数继续循环递归；这样，即使已经找出来了一种解法，程序也不会停下来，而是会继续寻找。如此，便能把所有的摆法全部找到，而且最多递归n次，因此所需要的空间不会太多。但是缺点是如果n超过了12，程序就会花费很长时间才能得出结果！！这就是这种方法的弊端，但至少也是一种办法。下面来看eightQueen()函数的精华部分：

for(j=0;j<n;j++){
	if(notEqual(row,j,n,chess)){//对一行中的每一个位置进行验证：若是可以放置皇后，那么就对棋盘进行更改；若不行，则继续寻找。
		for(i=0;i<n;i++)
			*(*(chess2 + row) + i) = 0; 
		*(*(chess2 + row) + j) = 1;
		eightQueen(row+1, n, chess2, count);//再次向后递归，这次注意：row变大了，预示着又往后走了一行，然后棋盘布局发生变化，然后函数还是一样的操作。核心就是棋盘的布局变了。
	}
}

总结

懂了吗？