第五章 字符串专题 ---------------- 5.12 字符串匹配之PabinKarp

题目：

假如要判断字符串A"ABA"是不是字符串B"ABABABA"的子串。

解法一：

暴力破解法， 直接枚举所有的长度为3的子串，然后依次与A比较,这样就能得出匹配的位置。 这样的时间复杂度是O(M*N)，M为B的长度，N为A的长度。

解法二：

       Rabin-Karp算法：

　　思想：假设待匹配字符串的长度为N，目标字符串的长度为M（M>N）；首先计算待匹配字符串的hash值，计算目标字符串前N个字符的hash值；比较前面计算的两个hash值，比较次数M-N+1：若hash值不相等，则继续计算目标字符串的下一个长度为N的字符子串的hash值，若hash值相同，则需要使用比较字符是否相等再次判断是否为相同的子串(这里若hash值相同，则直接可以判断待匹配字符串是目标字符串的子串，之所以需要再次判断字符是否相等，是因为不同的字符计算出来的hash值有可能相等，称之为hash冲突或hash碰撞，不过这是极小的概率，可以忽略不计)。

　　哈希函数定义如下：

　　其中Cm表示字符串中第m项所代表的特地数字，有很多种定义方法，我习惯于用java自带的char值，也就是ASCII码值。java中的char是16位的，用的Unicode编码，8位的ASCII码包含在Unicode中。b是哈希函数的基数，相当于把字符串看作是b进制数。h是防止哈希值溢出。 

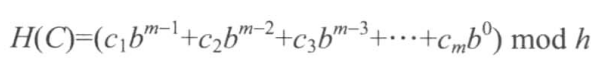
 代码：

public class RabinKarp {

    public static void main(String[] args) {
        String s = "ABABABA";
        String p = "ABA";
        match(p, s);
    }
    
    /**
     * @param p 模式
     * @param s 源串
     */
    static void match(String p,String s){
        long hash_p = hash(p);//p的hash值
        int p_len = p.length();
        for (int i = 0; i+p_len<= s.length(); i++) {
            long hash_i = hash(s.substring(i, i+p_len));// i 为起点，长度为p_len的子串的hash值
            if (hash_p==hash_i) {
                System.out.println("match:"+i);
            }
        }
    }

    final static long seed = 31;  // 进制数
    
    /**
     * 不同的字符计算出来的hash值相同 称为hash冲突
     * 使用100000个不同字符串产生的冲突数，大概在0~3波动，使用100百万不同的字符串，冲突数大概110+范围波动。
     * @param str
     * @return
     */
    private static long hash(String str) {
        long h = 0;
        for (int i = 0; i !=str.length(); i++) {
            // 这个计算方式就是 An²+Bn+c 的循环表达式，而这个计算方式就是二进制转十进制的计算方式 
            // 这里n=31，可以理解为转为31进制
            h = seed * h + str.charAt(i);
            
        }
        return h%Long.MAX_VALUE;  // 防止hash值过大
    }

}