ACL 2025｜MathFusion题目融合框架出炉，让大模型数学推理能力倍增

导言：

当前大模型的数学数据合成方法常常局限于对单个问题进行改写或变换，好比是让学生反复做同一道题的变种，却忽略了数学题目之间内在的关联性。 这种“单点式”的训练让大模型在面对由多个子问题组成的复杂场景时捉襟见肘，难以有效利用不同知识点之间的内在联系。 就像一个学生可能做独立的填空题可以做得很好，但是做包含多个有关联子问题的应用题时却很困难。

为了打破这种局限，让大模型学会“串联”与“并联”知识，我们提出了MathFusion，通过指令融合增强大模型解决数学问题的能力。受到人类学习过程中系统性接触关联的概念来提升能力的启发，MathFusion通过融合不同的数学问题来增强模型的数学推理能力。 仅使用45K的合成指令，MathFusion在多个基准测试中平均准确率提升了18.0个百分点，展现了卓越的数据效率和性能。

本研究成果《MathFusion: Enhancing Mathematical Problem-solving of LLM through Instruction Fusion》由OpenDataLab和人大高瓴等高校学院、研究结构联合提出，已被计算语言学和自然语言处理领域的顶级会议ACL 2025接收，欢迎关注。

论文链接：https://arxiv.org/pdf/2503.16212

代码链接：https://github.com/QizhiPei/MathFusion

---

一、MathFusion方法介绍

MathFusion是一种通过融合不同数学问题来增强大模型数学推理能力的全新框架，其核心思想在于以互补性数学指令的策略性组合来释放模型更深层次的推理能力。

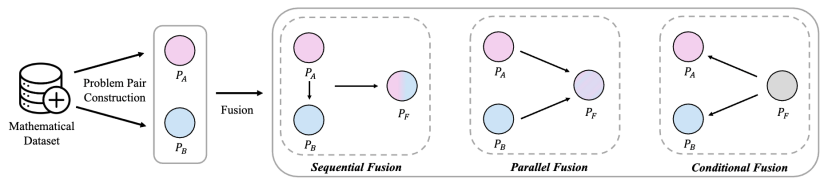
具体而言，通过三种“融合策略”，将不同的数学问题巧妙地结合起来，生成封装了二者关系和结构的新问题：

• 顺序融合 (Sequential Fusion)：将两个问题串联起来，前一个问题的答案作为后一个问题的某个输入条件。这就像解决一个多步骤问题，模型需要先解出第一步，才能进行第二步，从而学会处理问题间的依赖关系。
• 并列融合 (Parallel Fusion)：将两个相似的问题融合在一起，对它们的数学概念进行识别和融合，在原来问题的基础上提出一道新的问题。
• 条件融合 (Conditional Fusion)：创造一个需要对两个问题的解进行比较和选择的问题场景。

通过这三种策略，我们生成了一个全新的融合数据集MathFusionQA。 首先从现有数据集（GSM8K、MATH）中识别出适合融合的问题对（主要通过embedding search），然后应用融合策略生成新问题，并利用GPT-4o-mini来生成解答。

二、融合实例

通过整合两个现有问题，MathFusion 会合成一个新的数学问题，该问题涵盖了原始两个问题的关系性与组合性特征。

为了更直观地理解这三种融合策略，我们来看基于以上融合策略生成的新数学问题的具体例子：

原始问题

问题 A：一天内，一艘船在湖中航行4次，每次最多可载12人。请问在2天内，这艘船可以运送多少人？

问题 B：学校组织去博物馆。他们租了4辆巴士来接送孩子和老师。第二辆巴士的人数是第一辆的两倍，第三辆比第二辆少6人，第四辆比第一辆多9人。如果第一辆巴士上有12人，请问总共有多少人去了博物馆？

顺序融合后的新数学问题：

学校组织一次去博物馆的旅行，需要运送学生和老师。首先，请计算一艘船在2天内的载客量，这艘船每天航行4次，每次最多可载12人。然后，将这个总载客量作为第一辆巴士的人数。 已知第二辆巴士的人数是第一辆的两倍，第三辆比第二辆少6人，第四辆比第一辆多9人。请问总共有多少人去了博物馆？

如上所示，顺序融合后，问题A中船的总载客量作为问题B中的输入条件，即第一辆巴士的人数。

并列融合后的新数学问题：

一所学校组织一次到博物馆的实地考察，并租用了4辆巴士和一艘船。这艘船一天航行2次，每次载客12人。每辆巴士的人数不同：第一辆巴士有12人，...，第四辆比第一辆多9人。请计算在2天内，船和所有巴士总共可以运送多少人？

可以看到，并列融合后，生成了一道新的符合问题A和B原始语境的问题：计算运送的总人数。实际情况中，融合出来的新问题多种多样，这里以其中一个最简单的问题作为示例。

条件融合后的新数学问题：

一个社区正在组织两种不同的郊游活动。对于湖上游览，一艘船每天运营4次，载客量为12人，他们计划让这艘船服务2天。与此同时，一所学校正在安排一次有4辆巴士的博物馆之旅。 第一辆巴士有12人，第二辆是第一辆的两倍，第三辆比第二辆少6人，第四辆比第一辆多9人。考虑到这些安排，哪种交通方式的载客能力更强？

如上所示，条件融合后，新的问题要求模型结合语境，对问题A和B的结果进行比较和选择。

三、实验设置与结果

实验设置：

为了更好验证MathFution对于模型解决数学能力的增强作用，我们做了一系列的实验：

1. 从7B数学专用基础大模型DeepSeekMath-7B和7-8B通用基础大模型（Mistral-7B、Llama3-8B）出发进行训练。

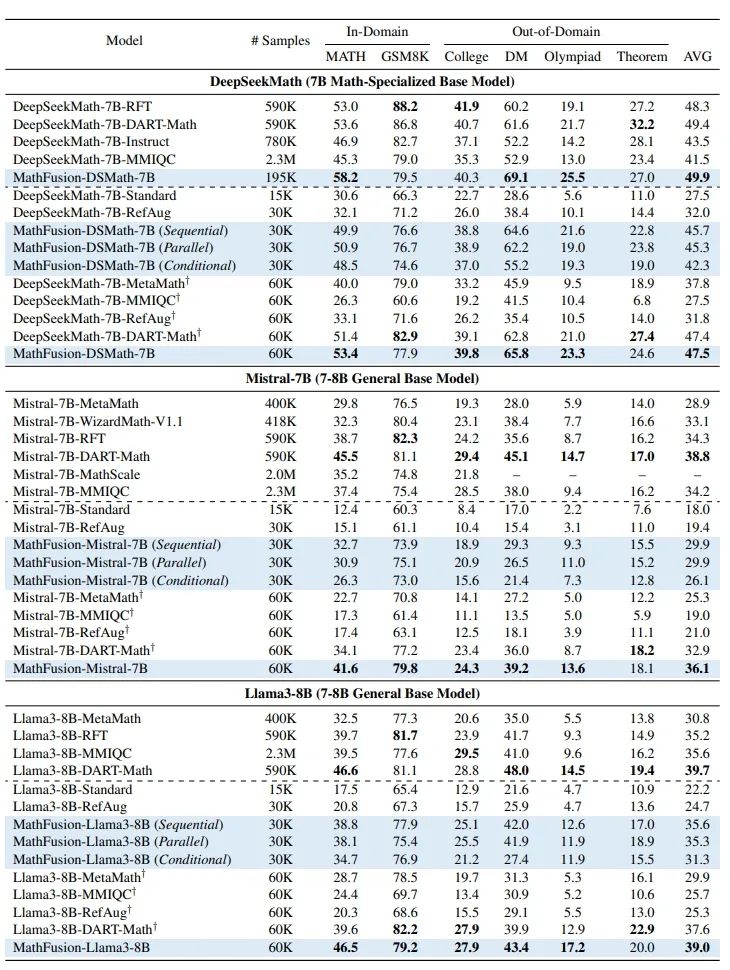
2. 每个基础模型均通过三种融合策略（顺序、并行、条件）进行微调。每种策略的微调数据集（30K样本）由 GSM8K、MATH 的原始数据集（15K样本）及对应融合策略生成的增强数据（15K样本）合并而成。MathFusionQA 数据集（60K样本）由所有子数据集合并构成。为验证 MathFusion 的Scaling能力，我们通过纳入Top-2至Top-4近邻样本扩大数据集，最终形成15K+4×(3×15K)=195K样本。所有模型均训练3轮完整训练。

3. 我们在两个领域内（In-Domain）基准测试GSM8K和MATH上评估模型。领域外（Out-of-Domain）评估采用CollegeMath、DeepMind-Mathematics、OlympiadBench-Math和TheoremQA基准。

4. 基线对比：我们主要将 MathFusion 模型与基于数学指令的模型进行比较，这些模型分为三类：

• 过往表现最优的方法：DART-Math、RefAug、MMIQC等

• 在GSM8K和MATH数据集上指令微调的模型（Standardard，15K样本）

• 基线方法的下采样版本（60K样本），以进一步评估不同数学数据增强方法的数据效率

实验结果：

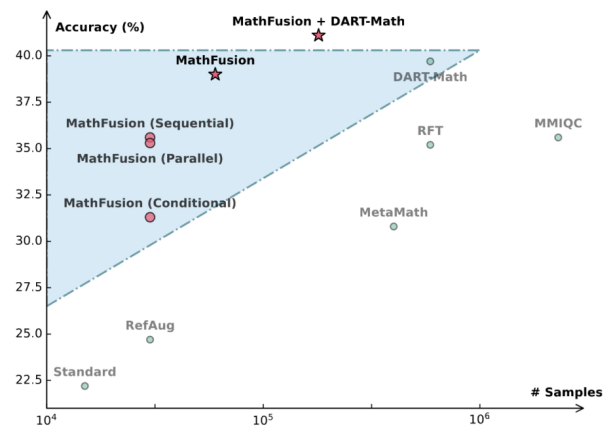
越靠左上角，模型表现越好且数据效率越高

显著提升模型性能与效率：与标准训练方法（只在GSM8K数据集和MATH数据集上训练）相比，MathFusion在多个基础模型（包括DeepSeekMath-7B、Llama3-8B、Mistral-7B）上都取得了稳定的性能提升。 更重要的是，MathFusion在大幅提升性能的同时，保持了极高的数据效率，用远少于其他方法的数据量就达到了良好的效果。

策略之间优势互补：由于三种融合策略捕捉了问题融合的不同方面，组合融合策略优于每种单一融合策略，表明三种策略的结合可进一步增强模型的数学能力。

强大的泛化与扩展能力：MathFusion不仅在in-domain测试中表现优异，在更具挑战性的out-of-domain基准测试中同样超越了标准模型。

我们做了进一步的分析，有如下几点发现：

• 融合之后的问题的指令遵循难度（IFD）更高，说明融合之后的问题对于模型来说更加困难。

• 随着融合数据量的增加，MathFusion模型的性能呈现出近似对数形式的增长。

• 当把MathFusionQA数据集与DART-Math数据集结合使用时，模型的性能可以得到进一步的提升，甚至超过了单独使用任何一个数据集时的表现。这表明MathFusion的“问题融合”思路与DART-Math的“挖掘难题”思路是互补的。

• 通过t-SNE可视化分析，我们发现MathFusion得到的问题在特征空间中的分布比原始问题更均匀和广泛。

• 通过对teacher model的消融分析，证明了MathFusion带来的提升源自于问题融合本身，而非teacher model的好坏。

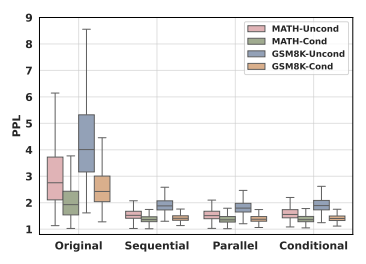
GSM8K和MATH数据集上原始数据与融合数据的无条件和条件困惑度 (PPL)

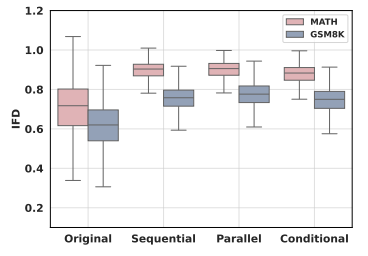
GSM8K和MATH 数据集上原始数据与融合数据的 IFD（指令遵循难度）

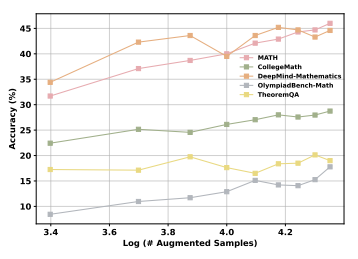
Llama3-8B模型在不同规模增强数据上的性能缩放表现 

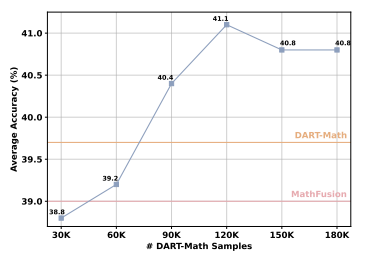
在MathFusionQA与DART-Math-Hard组合数据集上，使用不同规模采样数据微调Llama3-8B模型的平均性能

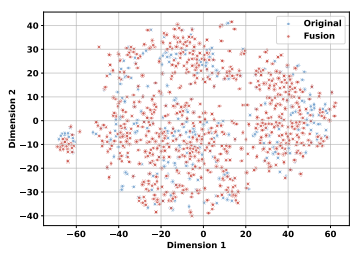
通过t-SNE对GSM8K数据集的问题嵌入进行可视化

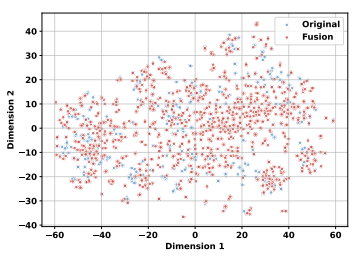
通过t-SNE对MATH数据集的问题嵌入进行可视化

四、总结

MathFusion提出了一种全新的数学数据增强范式，从“融合问题”而非“改造问题”的角度出发，为提升大模型的复杂推理能力开辟了一条新路径。通过生成结构更多样、逻辑更复杂的合成问题，MathFusion有效地增强了模型捕捉问题间深层联系的能力。但目前MathFusion还只在GSM8K、MATH这种比较简单的数学问题，以及short cot solution的数据集上进行了验证，有待进一步扩展到更难的数学问题、long cot solution以及其他领域的数据上。

更多关于MathFusion的使用方法和结果

欢迎访问以下地址👇

代码链接：https://github.com/QizhiPei/MathFusion