素数筛算法基础(一)

数组声明与初始化

数组就是相同类型一组变量的集合.是变量就会在内存上占用一定的空间大小;

    int a ;  //变量a 占 4个字节(32位);
    
    int a[100];// a[100]占 400个连续的空间;

求素数(关于数组的算法框架)

• 思路

初始化一个数组 , 元素全部标记为 0;
用 2 - n 的倍数去标记合数为1, 没有被标记过的数就没有因数,即为素数;
优化: 这里我们可以从1 遍历到 根号 n; 因为 列如 9 = 3*3; 一个数的因数是成对存在的,判断到一个数的 根号时没有因数就可以确定这个数是素数了
注意 : 1 既不是素数也不是合数;

(方法一:暴力遍历)

#include <stdio.h>
#include <math.h>
int is_prime(int n){
    for (int i = 2; i <= sqrt(n); ++i) {// 从2 判断到 根号n就可以判断N是不是素数,因为因素成对存在的.
        if(n % i == 0) return 0;
    }
    return 1;
}

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 2; i <= n; i++) {
        if(!is_prime(i)) continue;
        printf("%d\n",i);
    }
    return 0;
}

(方法二: 素数筛): 用素数去标记合数;
因为合数一定是能够由素数标记的,合数必有因数嘛,所以为了减少重复标记
我们可以,用素数去标记合数,这样能大大优化程序;

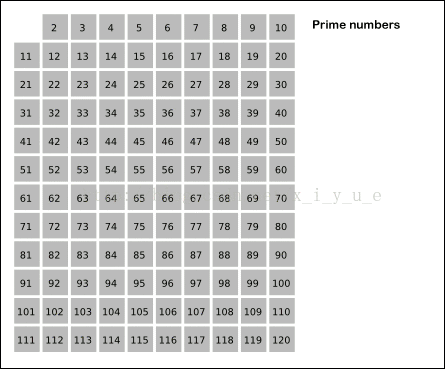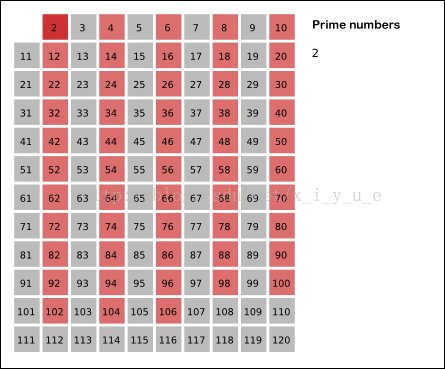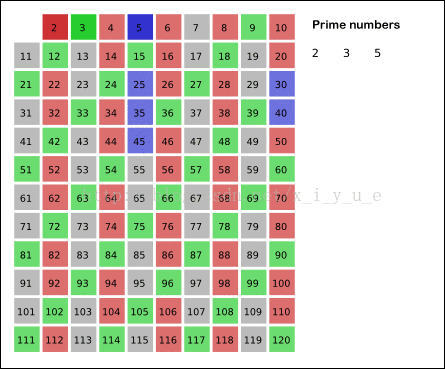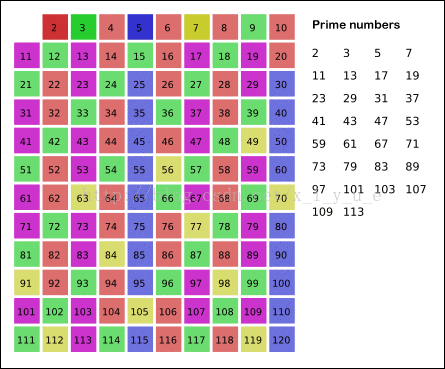
代码实现

#include<stdio.h>
#define MAX_N 100000
// 全局数组,系统会自己清为0,函数中不一定清;
int prime[MAX_N + 5] = {0}; //多开五位,初始化为0;

void init() {
    for (int i = 2; i <= MAX_N; i++){
        int cnt = 0;
        if (prime[i]) continue;//prime[i]被标记就continue;
        cnt += 1;
        prime[cnt] = i;
        //prime[++prime[0]] = i;//将素数个数存在prime[0]中;
       //for (int j = i * i; j <= MAX_N; j+=j) { j容易爆炸可以优化
        //prime[j] = i;
        for (int j = i ; j <= MAX_N / i; j++) {
            prime[j * i] = 1;
        }
    } 
    return ;
}
int main() {
 	init();
    //for (int i = 2; i <= MAX_N; i++) {
        //if (prime[i]) continue;
        //printf("%d\n", i);
    //}
    for (int i = 1; i <= prime[0]; i++) {
    		pritnf("%d\n", prime[i]);
    }
    return 0;
}

思考 : 用素数去标记合数虽然比暴力标记要好很多, 但是还是有很多重复标记比如:12可以被2和3标记,此方法时间复杂度为O(n*lglgn)，空间复杂度为O(n),基于此算法我们还能进一步将其改进成时间复杂度为O(n)的线性筛算法