什么是算法。算法的时间复杂度和空间复杂度

以图书馆为例，如果一本一本找累死人，要是有个索引，先找哪一类这样会快很多。如何查找其实就是算法。

算法是解决问题步骤的有限集合，通常用某一种计算机语言进行伪码描述。通常用时间复杂度和空间复杂度来衡量算法的优劣。

算法的五大特征：输入、输出、有穷性、确定性、可行性。

输入：零个或多个输入。

输出：一个或多个输出。

有穷性：有限步骤后在可接受时间内完成。

确定性：每个步骤都有确定含义，无二义性。

可行性：每一步都是可行的。

算法设计要求：正确性、可读性、健壮性、时间效率高和存储低。

正确性：有输入输出，无二义性，有正确答案。

可读性：方便阅读。

健壮性：输入不合法能处理

时间效率高和存储低：时间空间复杂度越低越好。

1.时间复杂度：

时间复杂度是一个函数，它定性描述了该算法的运行时间。

意义：同一问题可用不同算法解决，而一个算法的质量优劣将影响到算法乃至程序的效率。算法分析的目的在于选择合适算法和改进算法。
定义:
关于这是一个代表算法输入值的字符串的长度n的函数。

   时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。

   使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。

实例：
以冒泡排序为例，时间复杂度分析如下：

若文件的初始状态是正序的，一趟扫描即可完成排序。所需的关键字比较次数C和记录移动次数M均达到最小值：

所以，冒泡排序最好的时间复杂度为 O(n)

若初始文件是反序的，需要进行n-1趟排序。每趟排序要进行 n-1次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：


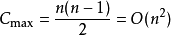
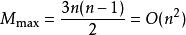
冒泡排序的最坏时间复杂度为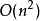

综上，因此冒泡排序总的平均时间复杂度为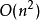

2.空间复杂度：

我们在写代码时，完全可以用空间来换去时间。

举个例子说，要判断某年是不是闰年，你可能会花一点心思来写一个算法，每给一个年份，就可以通过这个算法计算得到是否闰年的结果。

另外一种方法是，事先建立一个有2050个元素的数组，然后把所有的年份按下标的数字对应，如果是闰年，则此数组元素的值是1，如果不是元素的值则为0。这样，所谓的判断某一年是否为闰年就变成了查找这个数组某一个元素的值的问题。

第一种方法相比起第二种来说很明显非常节省空间，但每一次查询都需要经过一系列的计算才能知道是否为闰年。第二种方法虽然需要在内存里存储2050个元素的数组，但是每次查询只需要一次索引判断即可。

这就是通过一笔空间上的开销来换取计算时间开销的小技巧。到底哪一种方法好？其实还是要看你用在什么地方。

定义：
算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度的计算公式记作：S(n)=O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。
————————————————
版权声明：本文为优快云博主「萝卜头LJW」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/u013164931/article/details/80189351