数据结构和算法分析学习心得-二分查找篇(完结)

        之前写Java学习心得的时候吃了一个大亏，学习心得这个东西不能一下子积攒到一块去写，应该是每天学了一写知识点然后记一下，一些知识点忘了也可以回来复习一下，不然时间一长，有些忘掉的知识点还要回去翻找之前的视频，真的太浪费时间了，各位一定要引以为戒。当然了，这次的学习视频也是去B站找的黑马程序员的数据结构和算法Java。

2025年5月17日

二分查找算法

算法需求：在有序数组 A 内，查找值target

• 如果找到则返回索引
• 如果找不到返回-1

算法定义：

1. 前提条件：给定一个内含有 n 个元素的有序数组 A，满足 A[0] ≤ A[1] ≤ A[2] ≤ ...... ≤ A[n-1]，一个待查找值 target，数组里的值可以是相等的
2. 核心步骤：
3. 初始化左右边界索引 i = 0，j = n-1(n为数组长度)，i 为 left，j 为 right
4. 循环直到 i > j，未找到目标值，返回 -1（或表示未找到的标志）：
   1. 计算中间索引 m = (i + j) // 2  注意这里是整除2，也就是舍弃小数点后面部分
   2. 若 A[m](中间元素值) = target，返回 A[m]。 A[m]为中间元素值
   3. 若 A[m] < target，说明目标在右半部分，更新 i = m + 1。
   4. 若 A[m] > target，说明目标在左半部分，更新 j = m - 1。

代码演示：

​
/**
 * 二分查找基础版
 *
 * @param a 待查找的升序数组
 * @param target 待查找的目标值
 * @return
 *          找到则返回索引
 *          找不到返回-1
 */
public static int binarySearchBasic(int[] a, int target){
    int i = 0, j = a.length - 1; // 设置指针和初值
    while (i <= j) { // 范围内有东西
        int m = (i + j) >>> 1;
        if (target < a[m]) { // 目标在左边
            j = m - 1;
        } else if (a[m] < target) { // 目标在右边
            i = m + 1;
        } else { // 找到目标
            return m;
        }
    }
    return -1;
}

​

问题1：

• 其中 while 循环里 为什么是 i <= j，而不是 i < j 呢？
• 因为在查找 a[m] 时 i 和 j 有时会查找的是同一个元素，不光m会比较，i 和 j 也会进行比较，没有 = 就表示只有m进行比较，代码会报错。

问题2:

• 其中 int m = (i + j) >>> 1; 这一段中为什么不是 int m = (i + j) // 2;？
• 因为在Java语言中，正整数的最大范围为2147483647(32位二进制数)，超过这个范围，Java就会认为这个数的最高位是符号位。
• 比如 i = 1073741824，j = 2147483646，用原本int m = (i + j) // 2这种计算方式，计算出来m的结果为-1073741826，实际m的结果应为：3221225470(超过了Java正整数的最大范围)。
• 使用 int m = (i + j) >>> 1可以有效地解决这个问题。其中，>>> 是无符号右移运算符，它将十进制数的二进制表现形式整体向右移动一位，并在前面空出的位置补零。这样一来，原本超出范围的数就能被正确地表示出来。
• 比如上面提到的m的计算结果-1073741826，它的二进制表现形式1011_1111_1111_1111_1111_1111_1111_1110，整体向右移动一位就变成0101_1111_1111_1111_1111_1111_1111_1111，再转换成十进制表现形式是1610612735，这样计算结果m就能正常显示出来。

2025年5月21日更新

二分查找改动版

/**
     * 二分查找改动版
     *
     * @param a 待查找的升序数组
     * @param target 待查找的目标值
     * @return
     *          找到则返回索引
     *          找不到返回-1
     */
    public static int binarySearchAlternative(int[] a, int target){
        int i = 0, j = a.length;  //第一处
        while (i < j) {           //第二处
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m;            //第三处
            } else if (a[m] < target) {
                i = m + 1;
            } else {
                return m;
            }
        }
        return -1;
    }

对比原本基础版的代码可以看出改动这三处地方：

1. 第一处：
   1. 原本：int i = 0, j = a.length - 1;
   2. 改动后：int i = 0, j = a.length;
2. 第二处：
   1. 原本：while (i <= j) {...}
   2. 改动后：while(i < j) {...}
3. 第三处：
   1. 原本：j = m + 1;
   2. 改动后：j = m;

这三处改动有什么变化呢？

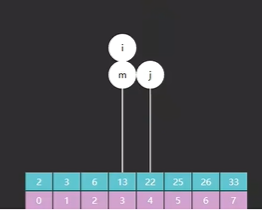
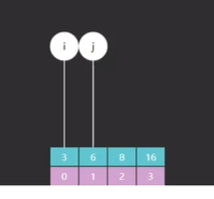
首先，i 和 j 他们所指向的索引元素不一样了，如图所示

图一

图二

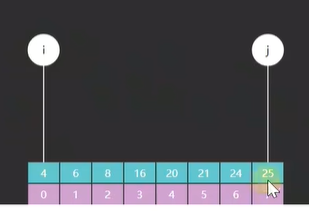
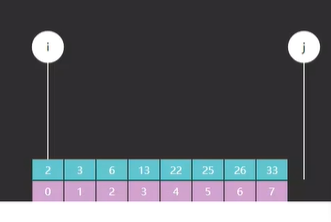
如图一所示的是原版 i 和 j 最开始指向的索引 0 和 7，而图二所示的是改版后的 i 指向的索引是 0 而 j 却指向了一个不存在的索引 8 ，为什么会这样？

 因为原版里 i 和 j 不光要作为边界，他们所对应的索引元素也有可能是我们的查找目标，而改版里 i 的功能不变，但是 j 就只作为边界，j 所指向的索引元素一定不是我们的查找目标(这句话一定要记住)。

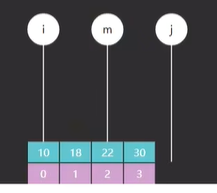
其次，比如我们现在要查找的目标值是13，中间值 m 最开始指向的元素是22，如图三

图三

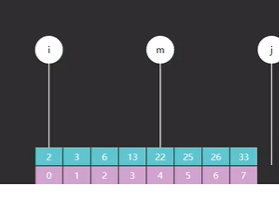
我们把目标值和 m 做一个比较，发现 13 < 22，需要向 m 左边查找，往左边缩小它的边界，那为什么是 j = m ?

因为改版的 j 只是作为一个边界，它所指向的元素一定不是我们要查找的值，如果用了原版的 j = m - 1，那 j 就会指向索引3的元素 13，13 就变成了不是我们要查找的目标值，语句就矛盾；而改版的 j = m，执行后 j 指向的是索引 4 的元素 22，而 m 和目标值不相等，所以 j 指向的索引元素不是我们要查找的值，语句不矛盾。

再执行一遍就发现，m 指向了索引 2 的元素 6，如图四，13 > 6，需要向 m 右边查，往右边缩小它的边界。

图四

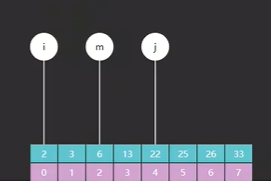
最后运行一遍发现，m 和 i 都指向了索引 3 的元素 13， 如图五 ，而 13 恰好就是我们要查找的值，至此代码运行结束。

图五

最后，再看一下为什么 while (i <= j) {...} 要改成 while(i < j) {...} ？

因为前面说过，i 是所指向的索引元素是有可能参与比较的，而 j 只是作为边界，不参与比较，如果让 i 和 j 相等了，那就跟 j 的定义矛盾了。而在有些情况下，i <= j 会让代码进入死循环，这一点需要注意。

​​​​

2025年5月24日更新

衡量算法的好坏

     /**
     * 线性查找
     *
     * @param a 待查找的升序数组(可以不是有序数组)
     * @param target 待查找的目标值
     * @return 找到则返回索引
     * 找不到返回 -1
     */
    public static int linearSearch(int[] a, int target) {
        for (int i = 0; i < a.length; i++) {
            if (a[i] == target) {
                return i;
            }
        }
        return -1;
    }

通过上面的线性查找算法和之前的二分查找-改动版对比，可以看出线性查找算法更为简洁，也不需要对数组里的元素进行升序要求，那是不是线性查找算法就比二分查找算法好？

不一定。

为了衡量一个算法的好坏，最直接的方法就是让它们各跑一遍，看谁运行的快，这种方法被称为事后统计法，这种方法随然直接，但是它也有缺点。

缺点一：

• 事后统计法比较依赖测试数据，一旦测试数据给的不好，不够充分，那我们也测不出来谁好谁坏，比如测试数据是一个很小的数字，这体现不出来谁快谁慢，或许它们的差距并不大；只有测试数据给的比较大的时候，才能看出来，好像是二分查找更快，但是准备测试数据又需要花费大量精力。

缺点二：

• 事后统计法还比较依赖电脑硬件环境，比如你自己在自己的电脑上写了个算法并运行，不一会就跑完了，但是你把这个算法放到那种硬件环境不怎么好的电脑上运行，可能它就需要运行半天才能跑完。

所以，我们要用一种叫做事前分析法的方法来衡量一下上面两个算法的好坏，通过方法的名字可以看出，我们并不需要实际去执行这个算法，而是通过分析的手段去预估出算法的执行事件，当然它也有两个前提条件。

条件一：

• 我们只分析这个算法的最差的执行情况，最好的情况和平均情况就暂时先不考虑，为了平衡，两个算法都只分析它们的最差执行情况。

条件二：

• 为了简化我们的分析过程，我们假设这两个算法每行语句执行的时间都是一样的，比如它们的赋值语句，比较语句，自增运算等，不然的话，我们还要考虑这个赋值语句和比较语句和自增运算它们之间的差异啊等，这样就把问题搞复杂化了，也就没法进行分析了。

首先我们来看线性查找算法

 public static int linearSearch(int[] a, int target) {
        for (int i = 0; i < a.length; i++) {
            if (a[i] == target) {
                return i;
            }
        }
        return -1;
    }

它的最坏执行情况是找不到结果，也就是所有循环都循环完后返回了一个-1，这种情况它执行的代码行数肯定是最多的，这是它最坏的执行情况，我们再来看一下他执行了多少行代码

线性查找算法运行次数

数据元素个数 n	执行次数
int i = 0;	1
i < a.length;	n+1
i++	n
a[i] == target	n
return -1	1

通过上面的表格可以看出，假设数组元素的个数是 n 个，代码每行语句的执行次数是这样的：

1. "int i = 0;" 临时变量 i 赋初值只执行一次
2. "i < a.length;" 判断 i 是否循环结束，要看它的执行次数和n的个数，所以这个比较运算执行n+1次，为什么要 +1 呢？因为当 i = a.length时，它就要退出循环了，但是 i = a.length 这个最后一次循环还是要有的，所以它总共执行的次数是 n+1 次
3. "i++" 数组内有 n 个元素，它就要自增 n 次
4. "a[i] == target" 这个比较语句里，每个数组元素都要和 n 比较，所以循环 n 次
5. "return -1" 最后都循环完了，没有匹配的结果，就要执行"return -1" 然后结束运行，所以它只执行1次

统计一下这个线性查找算法最差情况总共要执行的次数是 3*n + 3 次，我们发现它是跟我们数组元素的个数相关的，比如数组元素有 1000 个，它就要执行 3003 次

其次来看一下二分查找-基础版算法

    public static int binarySearchBasic(int[] a, int target){
        int i = 0, j = a.length - 1; 
        while (i <= j) { 
            int m = (i + j) >>> 1;
            if (target < a[m]) { 
                j = m - 1;
            } else if (a[m] < target) { 
                i = m + 1;
            } else { 
                return m;
            }
        }
        return -1;
    }

它的最坏执行情况有两种：

1. 跟线性查找算法一样，最坏执行情况是循环完后找不到结果，返回-1
2. 给定一个数组[2,3,4,5]，现在找target=1或target=6，这两种情况也是没找到，但它们的代码执行次数还不一样，而最坏的结果是右边 target=6 没找到(下面我们分析的时候以右边为准)

我们来看一下他执行了多少次代码：

1. "int i = 0, j = a.length - 1; " i 和 j 赋初值，所以执行 2 次
2.  "return -1;" 第一种最坏的情况是循环完后没有找到，返回-1，只执行 1 次

接下来看一下比较难确定的 while 循环里的情况

二分查找-基础版while循环语句运行次数

元素个数	循环次数
4-7	3
8-15	4
16-31	5
32-63	6
...	...

从上面的表格我们可以发现其中的规律，元素的个数和循环次数一个以 2 为底对数的关系也就是：log_2(n) + 1，拿4举例，它的以 2 为底对数的关系是：log_2(4) = 2，也就是说 4 要除 2 等于 1 需要除 2两次,最后再加上一个 1 就是我们要找的循环次数：log_2(4) = 2 + 1，以此类推：

• log_2(8) = 3 + 1
• log_2(16) = 4 + 1
• log_2(32) = 5 + 1

这时候有人要问了，5 和 7 除出来的不是整数啊？别急，对于这种情况，我们给它加一个floor()函数，让它向下取整，这样不就是整数了嘛，改完后的完整规律是：

• floor(log_2(4)) = 2 + 1
• floor(log_2(8)) = 3 + 1
• floor(log_2(16)) = 4 + 1
• floor(log_2(32)) = 5 + 1

我们再往下看while循环里的代码运行的次数

二分查找-基础版while循环语句里的代码运行次数

元素个数 n	执行次数 L
i <= j	L + 1
int m = (i + j) >>> 1	L
target < a[m]	L
a[m] < target	L
i = m + 1	L

通过上面的表格，我们假设元素的个数为 n ，执行次数为 L ，其中 L = [ floor(log_2(n)) + 1 ],他的while循环里的代码每行语句执行次数是这样的：

1. "i <= j" 循环执行次数是 L + 1 次，最后一次比较不成立才能退出循环，跟上面线性查找算法里的 i < a.length; 是一样的
2. "int m = (i + j) >>> 1" 求中间索引，执行 L 次
3. "target < a[m]" 判断目标值是否小于中间值，执行 L 次
4. "a[m] < target" 判断中间值是否小于目标值，执行 L 次
5. "i = m + 1" 中间值小于目标值条件成立，也是执行 L 次

最后统计出来这个二分查找-基础版算法最差情况总共要执行的次数是 (floor(log_2(n)) + 1) * 5 + 4 次

现在我们给出数组的个数是4这个条件，来看一下线性查找和二分查找基础版它们的代码运行的时间是多少，之前我们假设过它们的执行时间为 t ：

• 线性查找：3*4 + 3 = 15*t
• 二分查找-基础版：(floor(log_2(4)) + 1) * 5 + 4 = 19*t

这时候有人就要说：你看，线性查找好吧，它只需要15*t，这可不一定，这是数组个数比较小的情况下，比如，我现在再给一个数组个数 1024，再看一下它们执行的时间：

• 线性查找：3*1024 + 3 = 3075*t
• 二分查找-基础版：(floor(log_2(1024)) + 1) * 5 + 4 = 59*t

所以我们在衡量算法好坏的时候，不能光只看数据量比较小的情况，当数据量持续增大的时候，这个算法是不是依然能表现的很好。

为了能够更直观的看算法的好坏，我们可以通过这个网址来观察这两个算法的情况：Desmos | 图形计算器

两个算法的函数也放在下面了，各位可以复制到上面的图形网站里看一下它们长什么样子，能更直观的看到这两个算法随着数据量的增大，谁好谁差

线性查找：3*x+3

二分查找-基础版：(floor(log_2(x)) + 1) * 5 + 4

至于为什么要把n换成x，是因为Desmos图形网站只支持x，要用n的话，还需要单独添加一个 n = x 的条件，比较麻烦。

 2025年5月26日更新

时间复杂度

上面我们们通过一种叫事前分析的办法去衡量一个算法在时间上的好坏，这种分析方法在计算机科学有一个专门的术语：时间复杂度，下面说一下它的定义。

时间复杂度的定义：时间复杂度是用来衡量一个算法的执行，随数据规模增大，而增长的时间成本

这句话初看有些懵懵的，其实它的意思是：时间复杂度是用来衡量算法执行时间的好坏，如果数据规模不断增大，但算法的执行并没有明显的增长，那这种算法是就是比较优秀的算法。反之，随着数据量的不断增大，算法的执行时间明显增长，那我们说这个算法的时间复杂度高，它就是不怎么好的算法。

所以，总结一下，时间复杂度是衡量一个算法在时间上的好与坏的。

要注意，时间复杂度的分析过程是不依赖环境因素的，包括软件环境和硬件环境，其中，软件环境是指你的Java编译器有没有对你的代码做了优化处理，优化了，代码运行的速度就快了等，硬件环境是指你电脑的CPU主频，内存的存取速度等。

 所以分析时间复杂度的过程中，要把这些软硬件环境因素都忽略掉，只针对算法的本身来考虑它的执行时间的好与坏，不然还要考虑其它的各种环境因素，很麻烦。

那么该如何表示时间复杂度呢？

假设算法要处理的数据规模是 ，代码总共的执行行数用函数  来表示，例如：

• 线性查找算法的函数：
• 二分查找算法的函数：

但是，这两个式子看起来都相对比较复杂，不能一下子就看出这个式子代表的时间复杂度是高还是低或者说一下子抓不住其主要矛盾，所以我们要对  进行简化，用一个更简单的函数来代表我们数据规模增长跟增长的时间成本之间的一个变化关系，这个更简单的函数要跟我们 函数相近

所以接下来我们要用一种叫做大表示法的函数，用它来代表我们的时间复杂度。

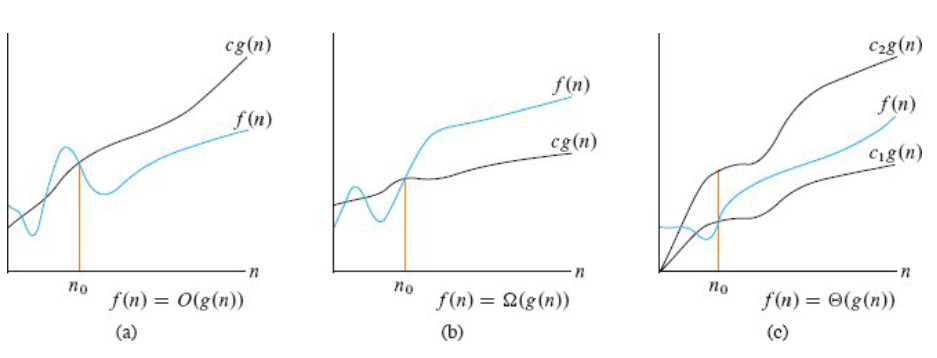
通过上面的图片来说明三个概念，首先说一下上图里的符号各自所表示的意思：

•   表示的是一些常数
• 表示的是数据规模，也就是对应着 x 轴
• 是实际执行代码的行数跟 n 的一个函数，表示的是算法执行时间与数据规模之间的一个变化趋势
• 是化简过后的函数，它的变化趋势是和 一致的，也是 n 的一个函数

接着我们来看图(a)，(a)的特点是 再乘以一个常数 后，在过 点之后，它的值都比 的值大，这样我们称 是 的一个上界，严格来讲叫渐近上界。

再看图(b)，(b)的特点是  再乘以一个常数 后，在过 点之后，它的值都比 的值小，这样我们称 是 的渐近下界。

最后看图(c)，(c)的特点是 再乘以一个常数 ， 后，在过 点之后， 的值比 的值小， 的值比 的值大， 和 把 f(n) 包围在中间了，这样我们称 是 的渐近紧界。

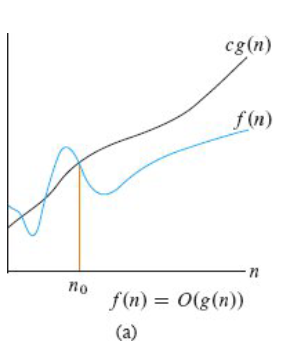
先来看渐近上界(Asymptotic Upper Bound)，它的符号表示是 ，它的含义是代表了算法最坏的执行情况，结合图(a)来看，图片里的 x 轴代表的是数据规模，y 轴代表的是这个算法实际执行的代码行数，y 轴的值越大，代表的实际执行代码行数越多，效率就更差。

我们以线性查找为例来说明 和 的关系，用图画表示

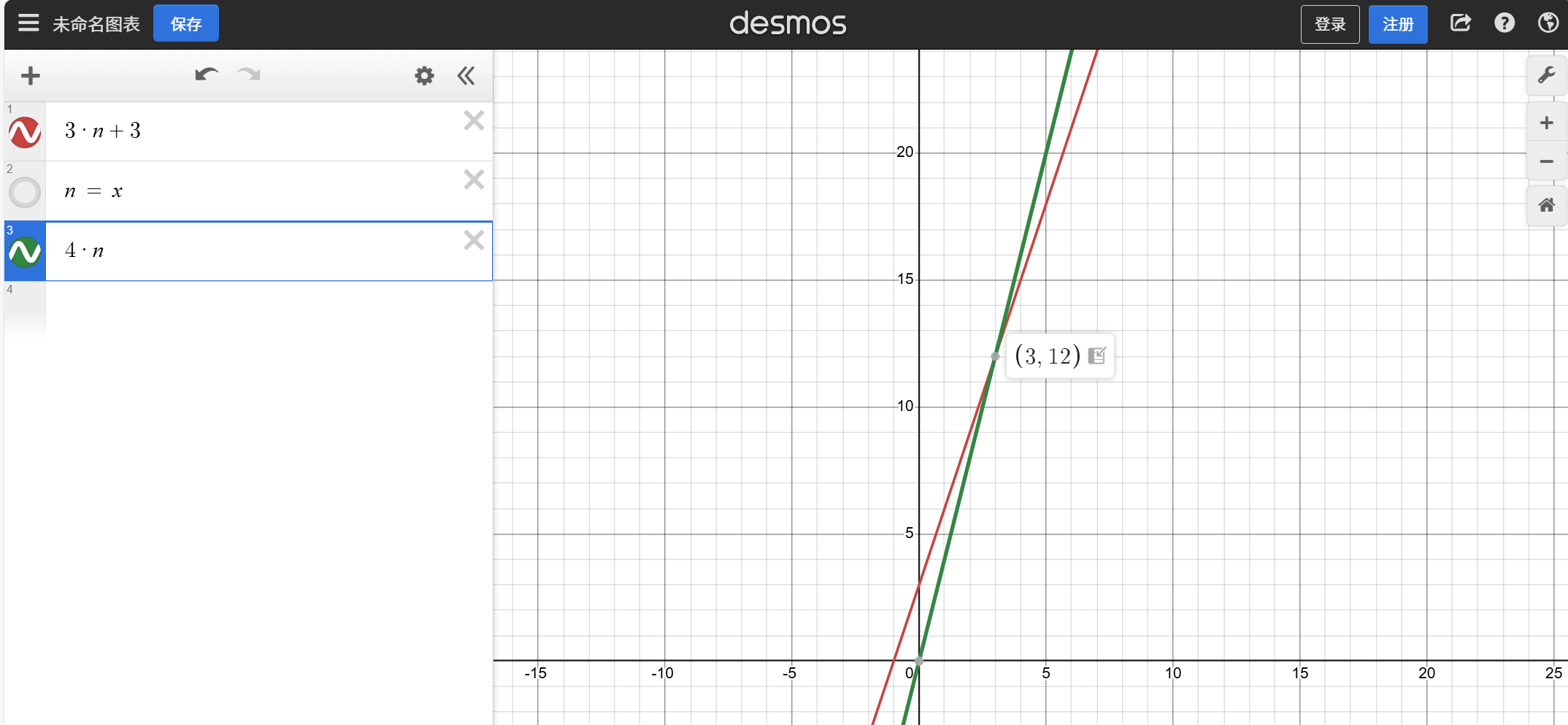
上图里，红线代表的是 ，绿线代表的是 ， 在过(3,12)这个点后，它的取值都在 上方， 函数就是 函数的一个上界，注意：这里 前面的常量系数绝对不能省略，一旦没有前面的常量系数， 不可能 比 大，这就和我们的介绍相反。

当然，我们用的大表示法表示的时候就不需要考虑常量系数 ，所以线性查找算法用大来表示就是 ===>

通过上面的例子我们可以看出 是比较关键的一点，那这个 函数是怎么来的，我们再多看几个例子就能明白了

下面我们以二分查找为例来说明 和 的关系，用图画表示

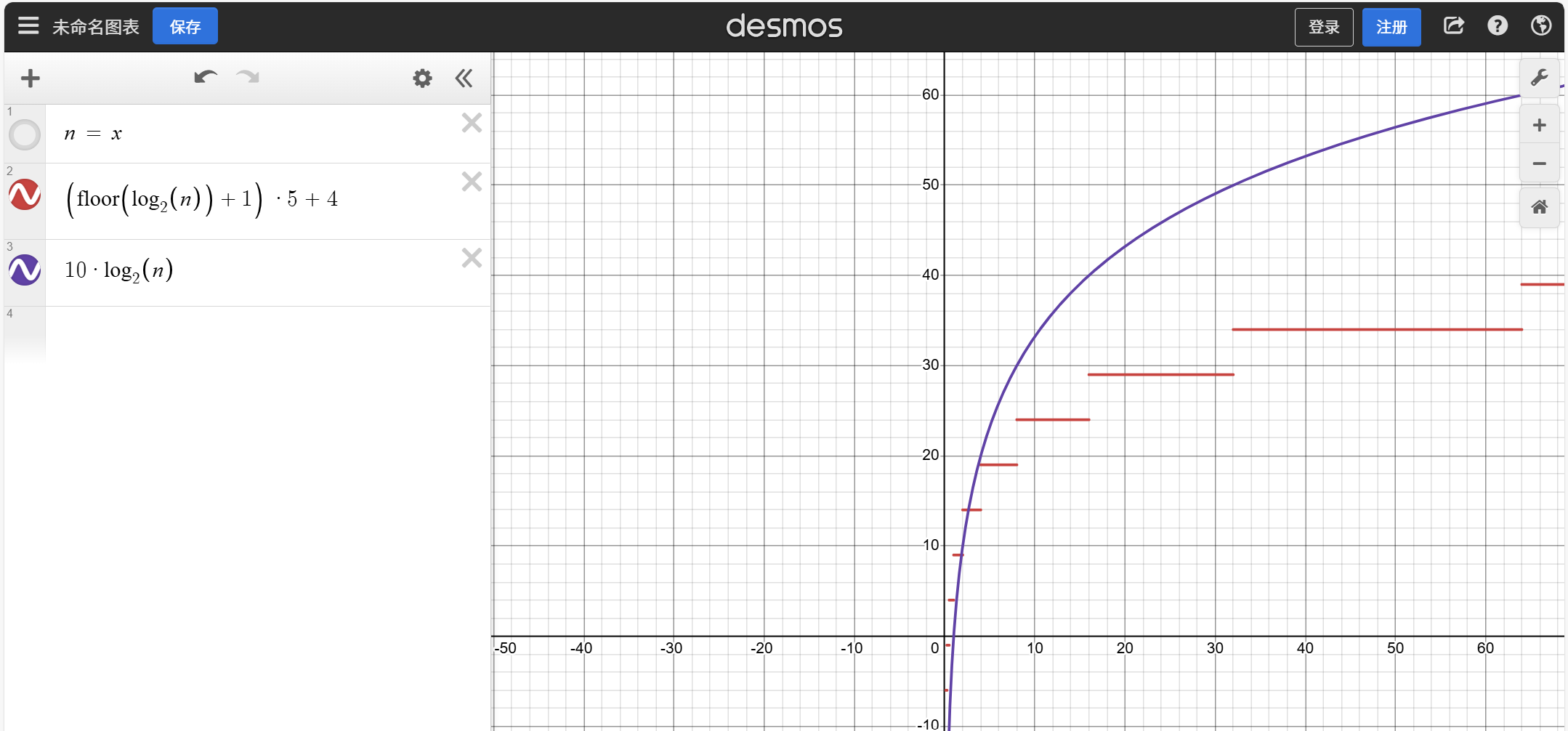
 红线代表的是 ，紫线代表的是 ， 在过大概某一点后，它的取值都在上方， 函数就是 函数的一个上界

二分查找用大表示法表示就是： ===>

下面我们来总结一下：

已知 来说，求

• 表达式中相乘的常量，可以省略，如
  •  中的 100
• 多项式中数量规模更小(低次项)的表达式，如
  • 中的 n
  • 中的
• 不同底数的对数，渐近上界可以用一个对数函数 表示
  • 例如： 可以替换为，因为 ，相乘的常量可以省略
• 类似的，对数的常数次幂可以省略
  • 如：

常见的大表示法

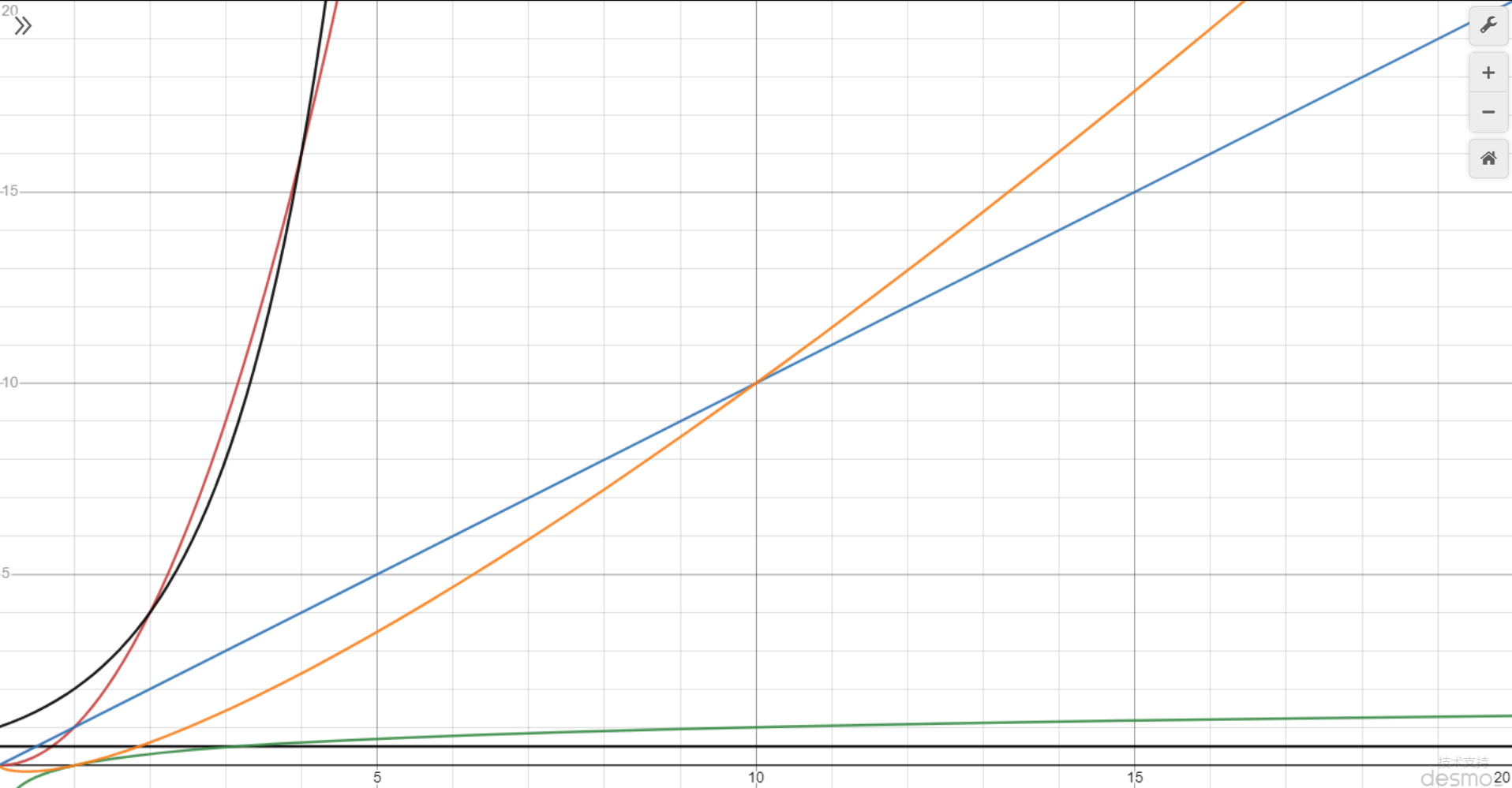
按时间复杂度从低到高

• 黑色横线，常量时间，意味着算法时间并不随着数据规模而变化
• 绿色，对数时间
• 蓝色，线性时间，算法时间与数据规模成正比
• 橙色，拟线性时间
• 红色，平方时间
• 黑色朝上，指数时间
• 没画出来的

上面就是常见的七种时间复杂度，一般来讲，如果某个算法能达到黑色横线和绿色这种第一档次的话，那这种算法的时间复杂度就算得上是非常优秀了，达到蓝色和橙色这种第二档次，那这个算法就比较一般了，达到红色和黑色朝上这种第三档次，这种算法就比较差的了。

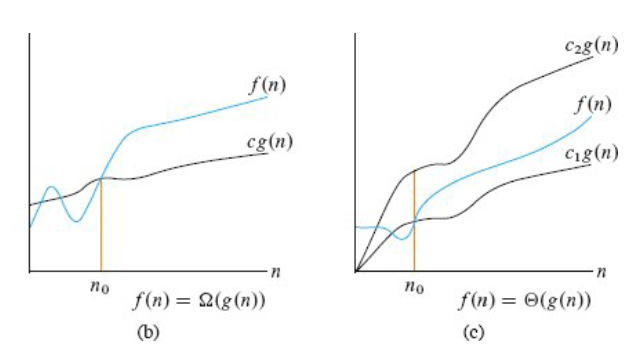
我们再来看一下最后剩下的渐近下界(Asymptotic Lower Bound)，渐近紧接(Asymptotically Tight Bound)。

先看渐近下界，从某个常数开始，总是位于下方，这种情况是算法执行最好的情况，记作。

最后看渐近紧界，从某个常数开始，总是在和之间，这种情况是算法既能有最好的情况又能有最差的情况，两种情况都能代表，记作。

2025年5月27日更新

空间复杂度

从字面意思上理解，空间复杂度就是衡量这个算法在空间占用上的好与坏，看以一下它的定义：与时间复杂度类似，一般也使用大表示法来衡量一个算法执行随数据规模增大，而增长的额外空间成本，原始空间不算在内。

    public static int binarySearchBasic(int[] a, int target){
        int i = 0, j = a.length - 1;    // 设置指针和初值
        while (i <= j) {                // i~j 范围内有东西
            int m = (i + j) >>> 1;
            if (target < a[m]) {        // 目标在左边
                j = m - 1;
            } else if (a[m] < target) { // 目标在右边
                i = m + 1;
            } else {                    // 找到目标
                return m;
            }
        }
        return -1;
    }

还是以二分查找为例来看一下它的空间占用，int[] a, int target这两个是初始数据，所以我们就看在这两个参数之外，还有哪些空间上的占有。

先看一下，i 指针， j 指针和 m 指针是不是要各占4个字节，把它们加起来，这个算法一共执行需要额外占用的字节数是12 个字节，其中循环里 m 不会产生新的 m，原因如下：在大多数语言里，这种占内存的情况，它会预先估算出这个方法内的这些局部变量会占用多少个空间，拿刚才的 m 举例，说这个循环内，m 实际上是不会重用这个空间的，它不会说循环一次占用四个字节，绝对不会。所以我们这个算法会额外占用的空间是 4 * 3 = 12 个字节。

那有人就要问了，那它占用的额外空间会不会随着数据的增大而增大呢？

答案是 不会。不管你这个数组再怎么变，比方说数组内的元素变成一万，变成十万，变成百万，这个 i j m 它们占用的内存是不变的，因此对于二分查找算法来讲，它的空间复杂度是大，它额外占用的只是一个常量空间，就是 12 个字节，不会再占用更多的空间了，也不会随着m的变化而变化，这就是二分查找算法的空间复杂度。

最后再看一下二分查找算法的性能

先回顾一下它的时间复杂度：

• 最坏情况：
• 最好情况：如果待查找元素恰好在数组中央，那么它只需要循环一次

再看一下空间复杂度：

• 需要常数个指针 i j m，因此额外占用的空间是

2025年6月18日更新

二分查找-平衡版

    public static int binarySearchBasic(int[] a, int target){
        int i = 0, j = a.length - 1; // 设置指针和初值
        while (i <= j) { // 范围内有东西
            int m = (i + j) >>> 1;
            if (target < a[m]) { // 目标在左边
                j = m - 1;
            } else if (a[m] < target) { // 目标在右边
                i = m + 1;
            } else { // 找到目标
                return m;
            }
        }
        return -1;
    }

我们先看第一个问题：现在我们需要在最基础的二分查找算法里去查它最左边的元素，假设我们已经知道了 while 循环的次数是 L 次，那么问题来了，while 循环里的 if else if 这些比较运算进行了多少次？

我们想一下，既然目标值最开始是在最左边，所以最开始 target 总是小于中间值的，那第一个 if 条件语句成立，它就会不断向左找直到找到最后一个；既然第一个 if 条件成立了，后面的 else if 还会执行吗？就不会了。

所以我们就能得出，如果这个元素在最左边，那它的比较运算 if else if 是不是也要运行 L 次？ 所以循环的最后一次就找到了。

我们再来看第二个问题：假如我们要查找的目标元素在最右边，它会比较多少次？

既然现在在最右边的话，那一开始 target 要比中间值大，所以第一个 if 条件语句不成立，它就会进入 else if 条件语句里，然后不断地向右找直到最后一次找到，所以元素在最右边的话，它既要执行 if 里面的比较，也要执行 else if 里的比较，所以它的总共比较次数是 2L 次。

总结一下，元素在最左边 if else if 循环是运行 L 次，元素在最右边 if else if 循环是运行 2L 次。

然后问题就出现了，我们现在的二分查找算法，它的左边找元素和右边找元素是不平衡的，向左找成本低，因为它只需要比较一次，而向右找的成本就高了，因为它需要比较两次，所以接下来要给出一个改进的二分查找算法来解决这个不平衡的问题。

    /**
     * 二分查找平衡版
     *
     * @param a 待查找的升序数组
     * @param target 待查找的目标值
     * @return
     *          找到则返回索引
     *          找不到返回-1
     */
    public static int BinarySearchBalanced(int[] a, int target){
        int i = 0, j = a.length;
        while (1 < j - i) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m;
            } else { 
                i = m;
            }
        }
        if (a[i] == target) {
            return 1;
        } else {
            return -1;
        }
    }

代码已经给出，我们来看一一下这段代码的含义，首先也是确定 i 和 j 这两个指针，这次的 i 和 j 是左闭右开的区间 [ i , j ) ，意思是 i 指向的有可能是我们要查找的目标，而 j 指向的肯定不是查找目标，比方说我们现在要查找的目标是3，而  i 指向的索引元素恰好就是3，而 j 指向的是一个空白的位置，这不是我们的目标，这是边界，如图6

图6

接着看 while 循环条件，发现和以前的不太一样了，j - i > 1是什么意思？意思是：j - i 就代表了这个范围内待查找的元素个数，这个数大于 1 的时候就不断地循环，不断缩小这个范围，也就是缩小这个区间，什么时候这个范围内只剩一个元素了 就退出循环

各位看图6里 i 和 j 的范围内是不是有四个待查找的元素，那它什么时候退出循环，我们直接跳到最后一步，你看这个时候它已经退出循环了，如图7

图7

为什么这个时候退出循环了？各位看 i 和 j ，i 指向的是范围内的元素，j 指向的不是目标，所以这个 6 肯定不属于我们的范围内对吧，所以这种情况下就意味着范围内就剩一个元素了，这个时候就退出了循环，这是while循环这块新写的条件的含义。

那这个改动后的算法的关键点在哪呢？它的关键点在于它并不是在我们的循环内就找出那个目标元素，它这个循环只是为了缩小边界，然后这个边界内什么时候就剩一个元素了，就剩 i 指向的元素了，这个时候他就退出循环，在循环外面去比较 i 指向的元素跟我们的目标是不是相同的，这个是改动后算法的一个关键点。

各位再看，刚才是我们这个范围内就剩一个元素了，它最后再去比较这个 a 指向的元素跟目标是否相同，有了这个前提，我们继续往下看这个循环内的代码是怎么写的。

首先去计算这个中间索引，这跟前面没啥区别，接下来看if else，已经没有那个else if了，这边要是多了一个else if，那它就是不平衡的，但是我们去掉了那个else if，它在这个循环内肯定只能做一次比较了，比较成功，走 if 里的语句，比较失败，走else里的语句，这样比较次数就平衡了。

我们解读一下这个新的 if else 的含义，来看这个 if 条件，它是说目标小于中间值，这和之前的语句一样，就意味着目标在中间值的左侧，既然在左边，那我们就要缩小右边界，让右边界 j 等于 m 这个和之前的二分查找改动版是一致的；但是下面的else的含义变了，由于没有了else if，所以如果进入了这个else里，那既有可能是 target 等于中间值，也有可能是 target 大于中间值，也就是说这个目标值有可能就在m，也有可能在m的右侧，这个时候我们就不能让 i = m + 1 了，必须让它变成 i = m ，为啥这样弄？

我们先举一个例子，比方说我们找一个目标值是 22，各位来看，这个时候中间索引 m 指向的是不是就是要查找的目标值，如图8

图8

因为目标值现在是 >= 这个中间值，所以会进入我们的 else ，进入 else 的时候，我们是不是就得让这个 i 留在 m 这个位置，如果 i 还等于 m + 1 ，那它就错过了 22，就跑到 30 上去了，因此我们else 这块复制语句变了，或者说这个 i 的变化的边界，得到把那个中间值包括在内，而不是变到中间值加1的位置，这是跟前面不一样的地方。

最后我们再来总结一下这个算法它的优缺点：

优点：这个算法的目的，就是减少循环内的比较次数，各位看，我们现在就剩 if else 了，所以每次循环它只需要比较一次了，在改动前它还有那个else if 的时候，如果目标值在左边的时候，我们只需要 if 那边的一次比较，但如果目标在右边的时候，我们肯定会进入那个 else if ，就要做两次比较了，所以说循环内的平均比较次数就减少了，这就是它的优点。

当然，话说回来，这个优点是必须在数据量比较大的时候才能够体现出来，如果数据量小，就体现的不是很明显。

缺点：我们在改动前分析这个二分查找时间复杂度的时候，我们提过一个最好情况，最好情况就是我们待查找的元素，如果恰好在数组中央的时候，直接判断出来中间元素和目标元素相等了，是不是直接就退出循环了，这时候只需要循环一次，所以这种情况下它的时间复杂度是，但是我们改动之后呢，前面也说了，它必须等到这个循环结束了，在循环外才能去比较这个 i 指针对应的元素跟目标元素，所以它就不存在刚才那种的时间复杂度了，毕竟时间复杂度最好跟最坏的情况全都是，这时候我们就可以换一种符号表示了，因为它的上界和下界都可以用同一种函数来表示，我们可以把它写成，这是改动后的版本。

它的时间复杂度的表示就是，这也算是它的一个缺点，不过这个缺点可以忽略。

2025年6月21日更新

二分查找-Java版

Java的二分查找在一个叫 Arrays 这个内容里，在 IDEA 里按下快捷键 ctrl + n 然后输入 Arrays，发现他是在 java.util 包下一个Arrays 类，如图9。

图9

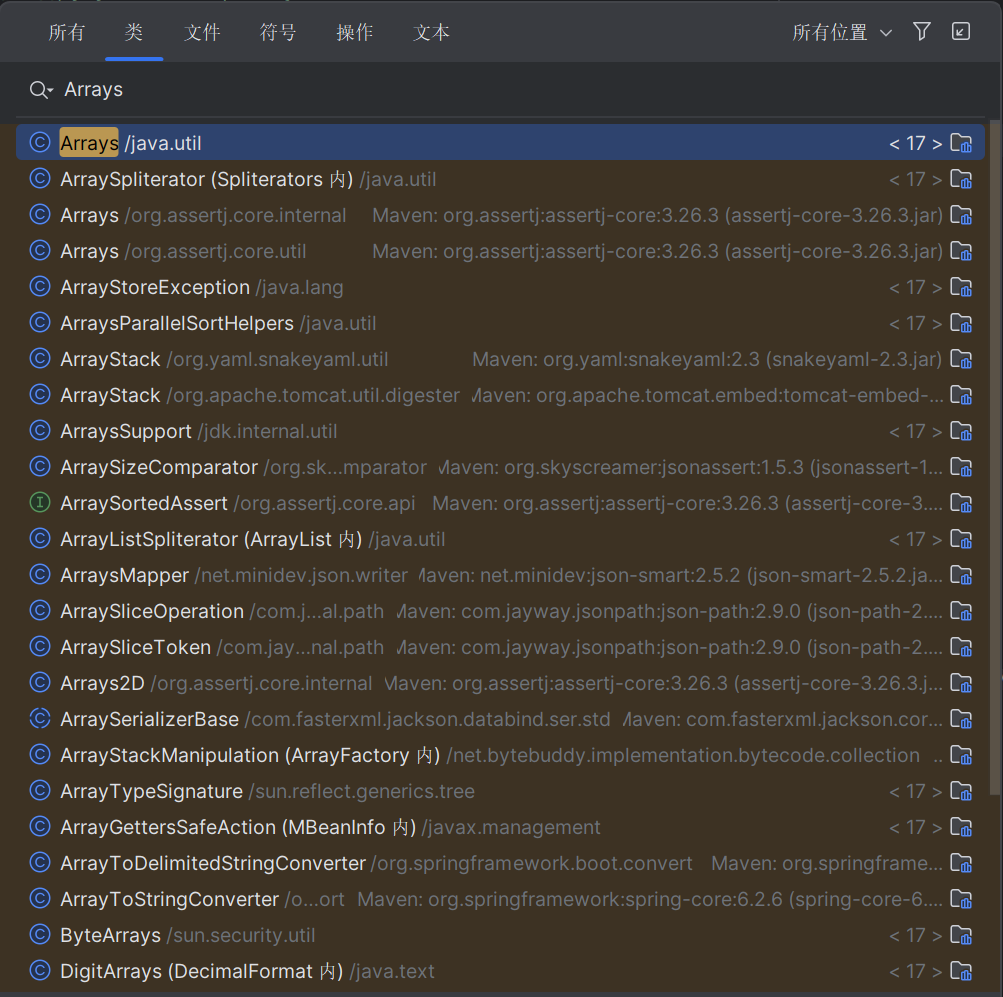
 我们先来看一下它的方法列表，按下快捷键 ctrl + F12或ctrl + Fn + F12，如图10。

图10

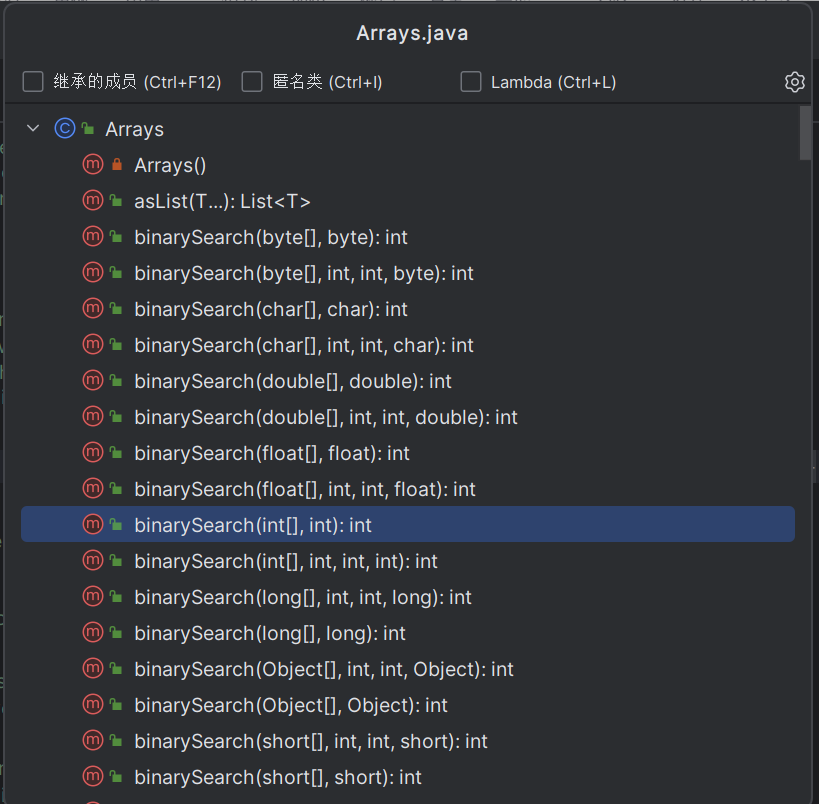
各位可以看到它的方法列表里有很多以 binary search 命名的方法，他们的主要区别在于处理的数据类型不一样，我们以其中熟悉的 int 数组的实现，我们来看一下他的参数，如图11。

图11

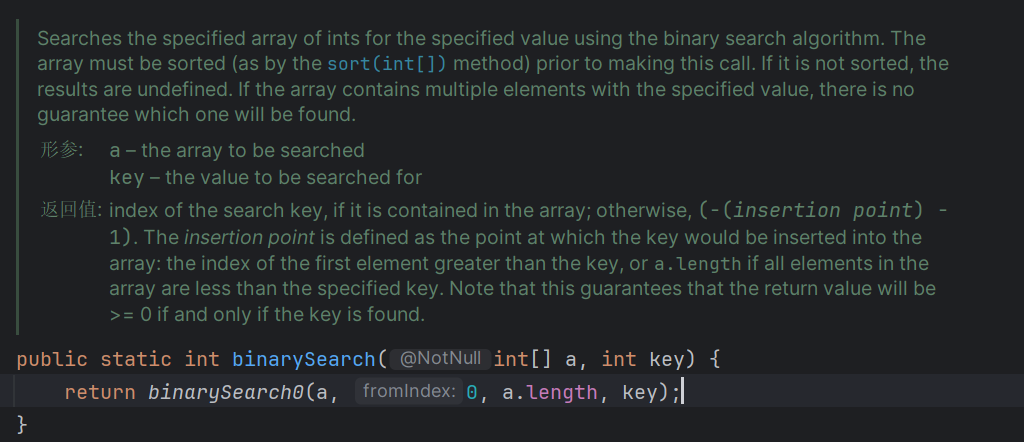
他的第一个参数 int[] a 就是待查找的数组，第二个参数 int key 就是要查找的目标值，只不过它的变量名和我们自己写的不太一样，我们叫 target，它叫 key，继续看它的内部，发现又调用了一个叫 binarySearch0 的方法，而且又多了两个参数，一个是 0 ，一个是数组长度 a.length。

我们接着看 binarySearch0 ，按住 ctrl 键再点击鼠标左键就可以快速跳到其所在的位置，如图12。

图12

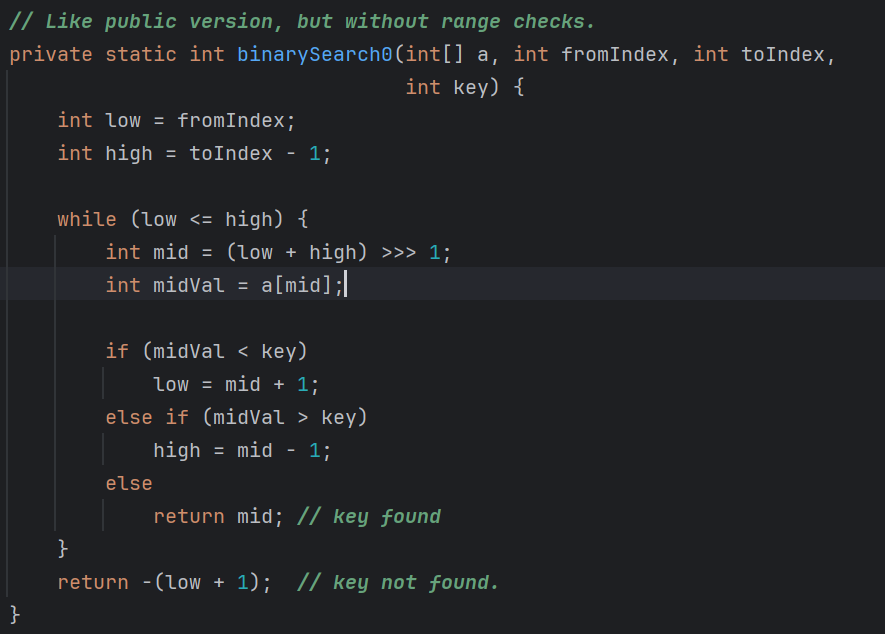
可以看到，在binarySearch0里 low 代表的是左边界，它的含义是和 i 一样的；high 代表的是右边界，它的含义是和 j 一样的，它俩的取值分别是源于 int fromIndex 和 int toIndex ，也就是 0 和 数组长度 a.length。

各位也发现了，它和之前写的二分查找基础版是一样的，所以 while 循环里 low 肯定小于等于 height ，因为基础版里 low 和 high 都可能指向要查找的目标，因此这个得有个等于条件保证最后它俩能相等时，他们指向的元素也要参与一次比较。

继续往下看，while 循环里是计算了一个中间索引 mid 同样这里也是使用了无符号右移运算来替换掉除法，这样可以避免出现负数的问题，下面是根据中间索引又拿到了中间值，再往下是中间值跟目标的比较，但是 Java 的这个习惯和我们的不太一样，我们是先看这个目标是不是在左边，再看目标是不是在右边，Java的是先看目标是不是在中间值的右边，在右边的话，那么左边界等于中间索引减一，如果 low 和 high 相等了，那就直接返回中间索引，它的算法的成本是向左找成本更高一些，因为向左找 Java 版是要比较两次，if 这比较一次，else if 这再比较一次，而向右找的成本就低一些，因为向右找只需要 if 这个比较一次。

从大体上看，Java 跟我们写的都差不多，除了比较的次序稍有不同，但是在循环结束后就不一样了，我们写的是没有找到的时候是直接返回一个 -1 ，但是 Java 版返回的是负的左边界加一，返回的是一个负数，那这个负数的含义是什么？

我们接着看，通过阅读这个 binarySearch 方法的文档 来理解一下它返回负数的意思，如图11 上面的绿色文档注释，翻译过来就是这个意思，如图13。

图13

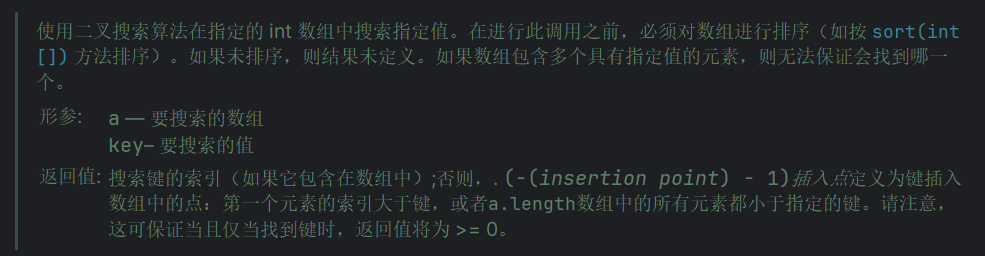
我们看到，翻译过来的文档，在返回值那边写着 返回的是 key 的索引，否则没有找到的话返回的是一个 -(insertion point)，意思是返回的是一个负的插入点再减去一个 1。

下面通过几个例子来明白这个插入点是什么意思，我们先看一段测试代码。

    @Test
    @DisplayName("binarySearch java 版")
    public void test8() {
        int[] a = {2, 5, 8};
        int target = 4;

        int i = Arrays.binarySearch(a, target);
        System.out.println(i);
        // -2 = -插入点 - 1
        // -2 + 1 = -插入点
    }

现在我们有了一个数组 {2, 5, 8} ，现在我要查找一个不存在的值，比方说查一个4，然后我们去调用一下 java 中它的这个 binarySearch，把我们的 target 作为参数放进去，那他运行后返回的是一个负数 -2 。

前面我们说了，Java 版没有找到所返回这个负数的含义是负的插入点，然后再减去一个 1，把这个负的插入点换算一下应该是这个 1 移到等式的左边来，就相当于 -2 + 1 = -1，这就是我们的负的插入点，然后再把前面的负号去掉就变成 1 了，也就是没有找到这个值，这个值后面要插入到这个有序或升序的数组中，它所插入的位置就是索引 1 的这个位置，也就是 {2, 4, 5, 8}。

我们再来一个例子，比如说现在我们要查找 1 ，结合上面的代码，我们所得到的结果是一个 -1，刚才我们说了，到最后都要加上一个 1，加上后就是 -1 + 1 = 0，所以这个插入点的值要插入到这个有序或升序的数组中，它的索引位置就是 0，也就是 {1, 2, 5, 8}。

最后来一个例子，现在我们查找的是 9，它最后运行的结果是不是 -4？ 因为他的索引位置是 3 嘛，也就是插入点位置是 3，取一个负号变成 -3，-3 - 1 就是 -4。

这就是 Java 版中，当找不到这个数组元素时，它返回负数的含义。

    public static int binarySearch(int[] a,int target) {
        int i = 0,j = a.length -1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m - 1;
            } else if (a[m] < target) {
                i = m + 1;
            } else {
                return m;
            }
        }
        return -1;
    }

下面我们再研究一下，当这个二分查找没找到时，上面代码里哪个变量可以代表这个插入点，我们先来看几个例子。

图14

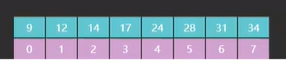
比方说，现在我们要查找一个 5，5 是不在这个数组里的，如图14，那么这个5后面要插入到有序数组的话，因该插入到索引 0 这个位置，而现在指向索引 0 这个位置的是 i，如图15。

图15

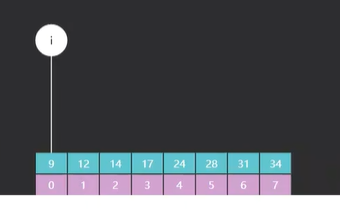
所以我们可以大胆的做一个假设，这个 i 就相当于这个插入点，接下来，我们再试几次，比方说，现在我们要找一个 20，这个 20 要是往这个有序数组插入的话，他插入的位置应该是 4，如图16。

图16

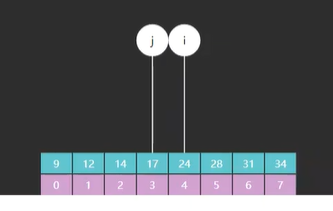
那我们再试些更大的值，就来个40吧，看一下这个40是不是也能用 i 来表示，如图17。

图17

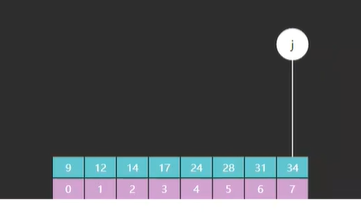
从图17我们看到，这个时候 i 就没有了，就剩一个 j 了，那我们回退一步，回退到 i <= j 的时候，这个时候 i 的值是不是指向的是索引7，如图18。

图18

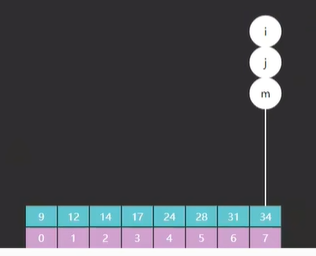
但是注意，因为我们要找的是 40，我认为它因该在右边，所以 i 接下来还要做一个 m + 1，也就是7 + 1 = 8 这个操作，8 这个操作执行完了后就退出循环了，由于图中的数组没有给出更大范围的数，所以退出循环，这个时候 i 也存在，也存在它的取值 8，这个 40 要是插入数组的话，它的索引就是 8，所以就证明了(不是严格的证明)对于这个种基础版的二分查找算法，这个插入点的位置就用变量 i 来表示。

我们再回到 Java 版的二分查找代码里，Java 版里的 low 的含义就跟我们基础版代码中 i 的含义是一样的，所以 low 就是我们的插入点，现在的Java版里这个返回值，它就说把 low 给变成负数，因为我们这个方法它返回 0 和正数表示的是他找到了，返回负数才表示没有找到，所以这个 low 要取个负数返回，这时候有人要问了，那我把 low 这个插入点取一个负数返回不就行了嘛，干嘛还要再让它加上一个 -1 呢？

事实上我们在这里给它加上了一个 -1，其目的就是为了区分插入点是 0 的情况，比如我们上面说过的找 5 的情况，它将来的插入点是不是 0，如果这个时候返回一个 -0，它其实跟 0 是区分不开的，因为计算机正数里 +0 和 -0 其实是一个值，我们写一个小代码来验证一下，如图19。

图19

各位可以看，鼠标移动到代码上时，显示始终为 “真” ，0 和 -0 其实是一个数，是无法区分开来的，所以我们找到的这个插入点，到底是表示找到了 0 索引的这个 9，还是说没有找到，返回了一个 0 这个插入点，这样子，这个插入点是不是就区分不了了，所以我们必须在这个插入点的基础上加上一个 -1，这样子呢，它才能够把它和找到的情况区分开来，这就是为什么要加 -1 的原因。

下面给各位看一下，如果已经拿到了这个二分查找的结果了，我们看看怎么进行插入操作。

    @Test
    @DisplayName("binarySearch java 版")
    public void test8() {
        /*
                ↓
            [2, 5, 8]      a
            [2, 0, 0, 0]   b
            [2, 4, 0, 0]   b
            [2, 4, 5, 8]   b
        */
        int[] a = {2, 5, 8};
        int target = 4;

        int i = Arrays.binarySearch(a, target);
        System.out.println(i);
        // -2 = -插入点 - 1
        // -2 + 1 = -插入点


        //新代码
        if (i < 0) {
            int insertIndex = Math.abs(i + 1); // 插入点索引
            int[] b = new int[a.length + 1];
            System.arraycopy(a, 0, b, 0, insertIndex);
            b[insertIndex] = target;
            System.arraycopy(a, insertIndex,b, insertIndex + 1, a.length - insertIndex);
            System.out.println(Arrays.toString(b));
        }
    }

通过上面新增加的的代码可以看到，如果这个 i 它的取值是小于 0 的，是不是就表示这个元素在这个数组里是没有的，没有找到的话就要进行一个插入操作，要插入的话，我们得要先找到它真正的索引值，那它的取值是不是就应该是这个 i 的返回值加上一个 1，所以是 i + 1，但是 i + 1 还有可能是负数，所以我们还要求一个绝对值，绝对值可以用 Java 中的 Math.abs() 函数，这样就求出它的绝对值，到这一步我们就得到了这个插入点真正的索引。

得到插入点索引后，我们接下俩继续来看，因为 Java 中的数组不能自动扩容，所以我们需要创建一个新的数组 b，把原来的数组 a 的内容拷贝进去，数组 b 的容量应该是数组 a 的长度加 1，然后我们先做第一步，我们用 System.arraycopy(); 就可以拷贝数组了，它的第一个参数是旧的数组 src；它的第二个参数是从索引 0 开始拷，因为我需要拷贝从起始位置到插入点位置的这些元素；他的第三个参数就是目标数据，也就是我们的数组 b；第四个参数是目标数组的起始索引，也是 0 索引，最后一个参数是拷的数据的长度，长度是不是就是索引位置减 0 就是我们的长度，减0是可以忽略的，所以就是 insertIndex，这一步相当于对应着我们把插入点之前的数据拷到新数组。

加下来看第二步，就是把我们新数组的插入点位置改成我们的目标值 target，这是第二步。

第三步就要把数组 a 的插入点之后的数据拷贝到新数组中，还是用 System.arraycopy(); 来拷贝，请注意，这回它的起点是插入点了，原数组里 5, 8 这个两个起点就是插入点这个索引，insertIndex 拷贝到数组 b，当然各位注意，数组 b 里的 5 和 8 是不是要在插入点加 1 这个位置开始拷贝，目标的起始位置应该是插入点加 1，所以正确的写法因该是 insertIndex + 1，要拷贝多长时间，是不是应该是 a.length 减去我们的插入点，原本 a 的数组长度是 3，减掉这个插入点就剩下 5 和 8 这个长度，这样我们就完成了。

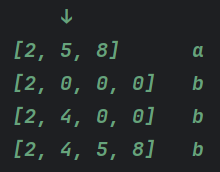
把 数组 b 内容打印出来就可以看到，新数组 b 的内容是[2, 4, 5, 8]，如图20。

图20

这里再多说一下拷贝数组的大致思路，我们以原本的数组 a 为例，原来数组 a 的内容是 [2, 5, 8] 那我现在要插入四怎么办？那我就需要创建一个比数组 a 容量更大的新数组，然后先把插入点前的这个元素拷贝到新数组去，假如我们这个插入点我已经知道了是 1 这个索引，先把插入点之前的元素 2 拷贝过去，这是新数组的内容，当然，新数组其他几个位置刚开始都是 0，这个新数组就是 [2, 0, 0, 0]这个样子，这是第一步；接下来我们就可以把这个 target 放到插入点这个位置，比如说他给的是 4，再把新数组插入点这个位置赋值为 target，这样新数组就是这个样子 [2, 4, 0, 0]，最后再把 a 这个旧数组插入点之后的 5 和 8 拷贝到新数组相应的索引位置，这时新数组就是这个样子 [2, 4, 5, 8]，通过这么几步我们就可以把这个数组进行一个插入的操作，这就是大致的思路，如图21。

图21

2025年6月25日更新

二分查找-LeftRightmost

    public static int binarySearch(int[] a,int target) {
        int i = 0,j = a.length -1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m - 1;
            } else if (a[m] < target) {
                i = m + 1;
            } else {
                return m;
            }
        }
        return -1;
    }

这次我们看一下二分查找算法对于重复的元素的处理，通过上面的基础的二分查找算法和给出的预定数组，如图22。

图22

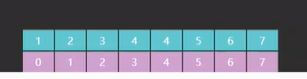
各位可以看到，这次给出的数组带有重复的元素了，对于这种重复元素的数组，二分查找算法会返回什么？我们举例说明一下，现在我要查找的元素是 4，运行之后中间索引 m 所指向的元素正好是索引为 4 的元素 4 如图 23，找到目标之后算法就不会再找别的数字了，就直接把结果返回了。

图23

所以，目前我们的基础版的二分查找算法，它遇到的重复元素就是返回它第一个找到的元素，其它的就不管了。那现在我需要提升一下我的需求，我要这个算法返回的重复元素是最左侧的元素，可能有些同志就要说了，你这图 23 里的重复元素不就是在最左侧吗？这个只是碰巧了，现在我把它改进一下，你看看还会是这样吗？

图24

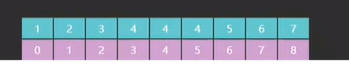
如图 24 所示，现在我已经往数组里多添加了一个元素 4，这次我们再看一下用二分查找基础版算法找到的是不是最左侧的 4，运行之后看图 25，我们可以看到这次 m 指向的元素 4 还是它第一次遇到的 4，并不是最左侧的 4，该如何改进？

图25

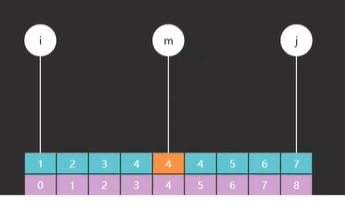
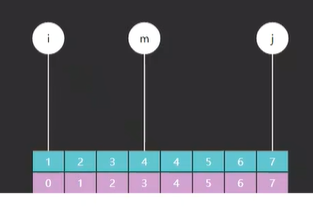
现在我们就要对原本的二分查找基础版算法进行改进，让它能找到这个重复元素里最左侧的元素，但不过在给出代码前，我们需要先看一下它实际运行的一个效果，然后通过这个效果来理解一下这个解题思路，我们还是查找这个最左侧的 4，第一步还是老样子先确定中间点，这样子中间点的元素跟目标是相等了，但它并不是我们最后要找的结果，那没有结果是不是就没用了？Nein！这个元素可以作为一个候选值，我们用橙色来表示，当然，这个候选值并不意味着这个算法的结束，所以我们还会向左侧继续找，来看有没有更左侧的 4，所以我们继续缩小 j 在左侧的范围，如图26。

图26

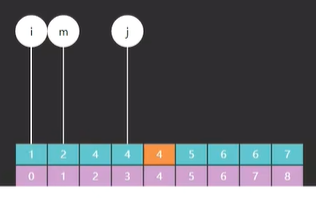
这次我们又找到一个中间点，很明显这次的元素跟我们的目标不等了，就需要让 i + 1 扩大 i，在这个范围里继续找，这次又找到一个中间点，这次 m 指向的元素又跟目标相等了，如图27。

图27

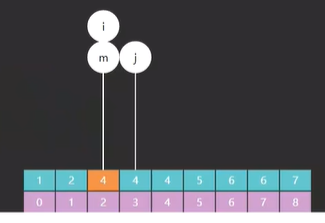
这回我们应该把刚才的位置记录下来，更新一下这个候选位置，这样我们就找到了一个更靠左的 4 这个元素，继续向做左找，再让 j - 1，这回 i 是不是就大于 j 了，如图 28 所示.

图28

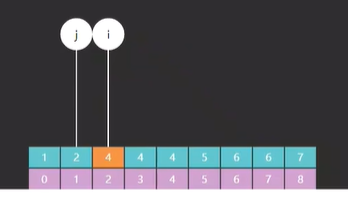
所以就该退出循环了，这时候我们候选记录的位置就是我们要查找的目标位置，理解了吧同志们。

我们可以再看一个，各位看数组里是不是还有个同样重复的老 6，同样的我们也来查找一下这个老 6，这个查找过程其实是类似的，也是先确定中间点 4，4 和 6 不相等，所以需要在中间点 4 的右侧来找，来缩小这个范围，第二次再找到这个中间点指向的元素是不是就跟目标值相等了，如图29，所以把它作为一个候选位置先记录下来，记录完后，我们再到它的左侧看有没有更靠左的 6。

图29

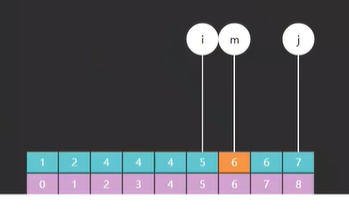
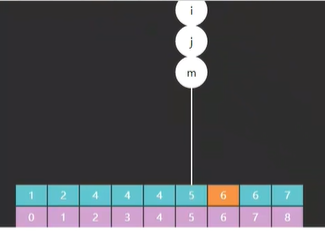
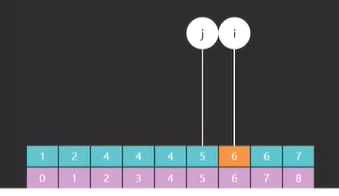
所以这回 j = m - 1后，再求这个中间点，发现是 5，如图30，这 5 和 6 不相等，需要我们去扩大 i，让 i = m + 1，现在已经是 i > j 了，如图31，所以就推出循环，这个时候候选位置指向的 6 就是最左侧的 6，这就是大致的思路。 

图30

图31

    /**
     * 二分查找 Leftmost
     *
     * @param a 待查找的升序数组
     * @param target 待查找的目标值
     * @return
     *          找到则返回索引
     *          找不到返回-1
     */
    public static int binarySearchLeftmost1(int[] a, int target) {
        int i = 0, j = a.length - 1;
        int candidate = -1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m - 1;
            } else if (a[m] < target) {
                i = m + 1;
            } else {
                // 记录候选位置
                candidate  = m;
                j = m - 1;
            }
        }
        return candidate;
    }

上面给出的代码就是找最左侧重复元素的代码，Leftmost就是靠左的意思，这个代码是在二分查找算法的基础上进行了一下小改动，改动了 else 这个位置，原本是找到了直接返回 m，现在是改成了找到后，先把这个 m 指向的位置先记录下来，作为一个候选位置，因为你不能确定它左边有没有更靠左的元素，所以我们需要定义一个变量用来记录这个候选位置，变量名 candidate 是候选者的意思，刚开始它的初值是 -1，表示没有任何的候选者，当我们的中间值 m 它指向的值和目标值相等了，那就让 candidate 的取值等于 m，这样就把这个位置记录下来，记录完后，我们还需要继续向左侧查找，所以需要缩小 j 这个边界，让它等于 m - 1，没有问题的话继续缩小 j 的边界，如果我们遇到了新的 m 他指向的值和目标相等了，那它又走到 else 了，这个时候就更新候选位置，当 i > j 的时候，循环结束退出，这时候返回候选位置就可以了，因为它记录了我们最靠左的重复元素的位置，当然没有找到就返回它的初始值 -1。

    @Test
    @DisplayName("binarySearchLeftmost1 返回 -1")
    public void test6() {
        int[] a = {1, 2, 4, 4, 4, 5, 6, 7};
        assertEquals(0, binarySearchLeftmost1(a, 1));
        assertEquals(1, binarySearchLeftmost1(a, 2));
        assertEquals(2, binarySearchLeftmost1(a, 4));
        assertEquals(5, binarySearchLeftmost1(a, 5));
        assertEquals(6, binarySearchLeftmost1(a, 6));
        assertEquals(7, binarySearchLeftmost1(a, 7));

        assertEquals(-1, binarySearchLeftmost1(a, 0));
        assertEquals(-1, binarySearchLeftmost1(a, 3));
        assertEquals(-1, binarySearchLeftmost1(a, 8));
    }

通过上面给的测试案例，我们来运行一下看看这个代码的正确性，现在我们有了 {1, 2, 4, 4, 4, 5, 6, 7} 这么一个数组，我们要查找 1，它返回的是不是就是 0，我们要查找 2，它返回的是不是就是 1，我们要查找 4，它返回的是不是就是 2 等等，这是找到的情况，当然我们也给了没有找到的情况，0 3 8 它们都不在数组里，它们返回的都是 -1。

    /**
     * 二分查找 Rightmost
     *
     * @param a 待查找的升序数组
     * @param target 待查找的目标值
     * @return
     *          找到则返回索引
     *          找不到返回-1
     */
    public static int binarySearchRightmost1(int[] a, int target) {
        int i = 0, j = a.length - 1;
        int candidate = -1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m - 1;
            } else if (a[m] < target) {
                i = m + 1;
            } else {
                // 记录候选位置
                candidate  = m;
                i = m + 1;
            }
        }
        return candidate;
    }

同样的，既然有重复元素里找最靠左的，同样的因该还有一个叫 Rightmost 的，它是重复元素里找最靠右的，大致代码都是类似的，我们也是要用一个 candidate 来记录他的候选位置，这个候选位置同样的也是当我们每次这个中间值跟这个目标相等的时候，要把它记录下来，要更新这个候选位置，只不过每次发现相等了，我们要向右找，也就是让 i 的边界扩大，让 i = m + 1 不断的向右找，直到找到最右侧的这个候选者，当然了，如果都找不到这个候选位置，那就返回 -1。

    @Test
    @DisplayName("binarySearchRightmost1 返回 -1")
    public void test7() {
        int[] a = {1, 2, 4, 4, 4, 5, 6, 7};
        assertEquals(0, binarySearchRightmost1(a, 1));
        assertEquals(1, binarySearchRightmost1(a, 2));
        assertEquals(4, binarySearchRightmost1(a, 4));
        assertEquals(5, binarySearchRightmost1(a, 5));
        assertEquals(6, binarySearchRightmost1(a, 6));
        assertEquals(7, binarySearchRightmost1(a, 7));

        assertEquals(-1, binarySearchRightmost1(a, 0));
        assertEquals(-1, binarySearchRightmost1(a, 3));
        assertEquals(-1, binarySearchRightmost1(a, 8));
    }

向右查找的测试案例也给出了，各位可以自己去运行一下看看是不是能通过。

2025年7月29日更新

二分查找-LeftRightmost返回值

之前我们说过 Rightmost 版本和 Leftmost 版本，其中 Rightmost 版本它是查找与目标相等的最靠左的索引，找不到则返回 -1，Leftmost 版本是查找与目标相等的最靠右的索引，找不到也是返回 -1，各位看到这两个方法在找不到的情况下都返回的是 -1，在往后面学习时，大家都会发现它返回的这个 -1 没什么用，所以我们可以让这个两个方法返回一个比 -1 更有用的值，下面就以 Leftmost 为例来改动这个代码。

    public static int binarySearchLeftmost2(int[] a, int target) {
        int i = 0, j = a.length - 1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target <= a[m]) {
                j = m - 1;
            } else {
                i = m + 1;
            }
        }
        return i;
    }

改动后的代码也已经给出，我们可以测试这个代码去理解它返回的这个 i 的含义，用来测试的数组也已经给出，如图32。

图32

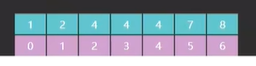
 现在我们要查找 4，直接看最后一步如图33。

图33

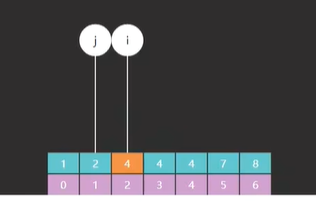
可以看到最后一步 i 指向的索引位置代表的也是与目标相等的，最靠左的索引位置，这个和改动之前是一样的，所以 i 跟前面方法返回值的含义是一样的。我们再来看一个没找到的情况，就找 3，3是不在这个数组里的，同样也是直接看最后一步，如图34。

图34

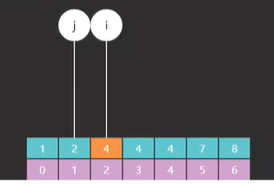
各位可以看到这个 i 还是指向了 4，这个该怎么理解？各位可以这么理解，它是找到一个比目标大的，注意我们的目标是 3，比目标大的就是 4，并且也是最左侧的索引位置 ，其中 “找到一个比目标大的，并且是最靠左侧的索引位置” 这句话就是在没有找到的情况下的含义，如果各位觉得不靠谱，我们不妨再试一个，这次就找 5，5 同样也不在数组里，按照我们刚才说的方法去查找的话，结果是不是应该在 7 这个位置，如图35，各位把前面的话带入到 5 这个例子里 “比5大的，最靠左的” 是不是就是 7。

图35

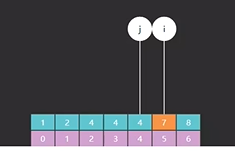
我们总结一下，找到的情况是与目标相等的，最靠左的索引位置；没有找的情况是比目标大的，最靠左的索引位置。我们返回的这个 i，它代表的就是大于等于目标的，最靠左的索引位置。

    /**
     * <h3>二分查找 Leftmost</h3>
     *
     * @param a 待查找的升序数组
     * @param target 待查找的目标值
     * @return
     *          <p>返回 ≥ target的最靠左索引</p>
     */
    public static int binarySearchLeftmost2(int[] a, int target) {
        int i = 0, j = a.length - 1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target <= a[m]) {
                j = m - 1;
            } else {
                i = m + 1;
            }
        }
        return i;
    }

改动后代码的注释给大家写好了，对于我们改动后的这个 Leftmost 版本来讲它返回的这个 i 代表的含义是大于等于目标的，并且最靠左的一个索引位置。

    /**
     * <h3>二分查找 Rightmost2</h3>
     *
     * @param a 待查找的升序数组
     * @param target 待查找的目标值
     * @return
     *          <p>返回 ≤ target的最靠左索引</p>
     */
    public static int binarySearchRightmost2(int[] a, int target) {
        int i = 0, j = a.length - 1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m - 1;
            } else {
                i = m + 1;
            }
        }
        return i - 1;
    }

 Rightmost改动后的版本也已经给出，同样也来进行测试，看看改动后的 i - 1 是什么意思，测试的数组还是图32里的数组。

老样子，还是找 4，直接看结果，现在指向的索引的位置是 5，5 - 1是不是最右侧的 4，如图36。

图36

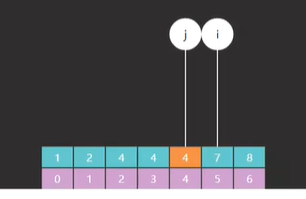
所以它跟改动之前的意思也是一样的，代表的是与目标相等的最靠右的这个位置；同样再看一个不存在的，还是找 5，看到结果跟刚才一样，连位置都没有变，如图37。

图37

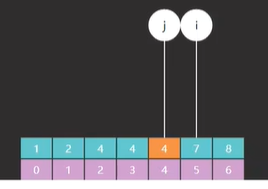
这个改如何理解 i - 1 的含义呢？可以这么理解，当我们找一个不存在的值，这个时候它就是找比目标小的，并且是最靠右的元素，把 5 带进去看就是，我们要找的是 5，4 是不是比 5 小，而 j 指向的 4 是不是 比 5 小且最靠右的元素？所以这个位置就是索引4这块。

最后总结一下，改动后的 Rightmost，返回值是 i - 1，它代表的是小于等于目标的，最靠右的索引位置，这就是 i - 1 的含义。

2025年8月4日更新

LeftRightmost应用

有人或许要问，前面不是说过二分查找 LeftRightmost 返回 -1 没什么用吗？那修改后的返回值又有什么用？
你别说，这用处可大着呢，我们可以用他们去求排名，求前任和后任，求最近邻居以及做一些范围查询等，到这里估计有人又要问了，你这排名，前任，后任，最近邻居都是什么东西？各位别急，请让我慢慢地解释。

我们先看排名，它的意思是说我有一个 target 值，我希望看看在这个数组里这个target值排名第几？先给出一个数组，如图38。

图38

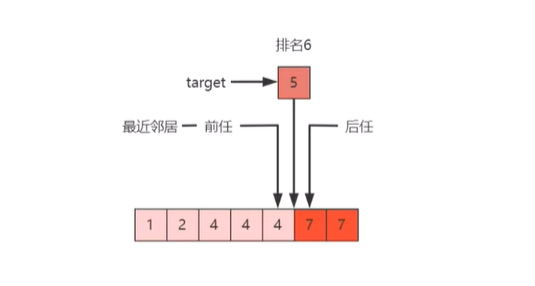
比如说这个图里的 5，它的排名就是 6，那为什么是 6？各位看一看比 5 小的元素是不是有 5 个，所以 5 的排名就是 6，在比如说我要找 4，比 4 小的元素是不是有 2 个，所以 4 的排名就是 3，这样能理解吧。

我们再看这个前任和后任，注意，这个前任和后任不是你脑子里想的前任和后任。这里的前任意思是比 target 小的并且在数组最靠右的元素，这叫前任，各位看在图 38 的数组里比 5 小的是 4，那比 5 小且最靠右的 4 是不是排名为 5 的 4，而排名为 3 和排名 4 的 4则叫前前任和前前前任了。

同理，后任就是比 target 大的且在数组里最靠左的元素，这叫后任，各位看在图 38 的数组里比 5 大的是 7，那比 5 大且最靠左的 7 是不是排名为 7 的 7，而排名为 8 的 7 则是后后任。

什么叫最近邻居，它的意思是前任和后任加在一块，看谁更小，谁离 target 更近，就那图 38 的例子来说，排名 5 的 4 跟排名 6 的 5 中间是不是距离了一个位置，排名 7 的 7 跟排名 6 的 5 中间是不是距离了两个位置，所以我们说排名 5 的 4 就是 排名 6 的 5 的最近邻居。

解释完了这几个新增的词，我们来看第一个问题：求排名，各位想一下，我要求排名的话，是用前面说过的 Leftmost，还是用 Rightmost？如果忘掉 Leftmost 和 Rightmost 的同志请看图 39。

图39

比如说我想求四的排名，那我是不是要找到在这个数组里最左侧的 4，这样我才能知道它的排名为 3，所以我们应该用 Leftmost 的版本，我们把 4 这个参数传进 Leftmost() 里，求出来最左侧的 4 的索引为 2，可能有有要问了，为什么这个 4 的索引是 2，排名却是 3，这怎么还差个 1？因为数组的索引是从 0 开始，而排名是从 1 开始的，所以我们在索引 2 的基础上再加一个 1 就可以得到排名 3 了。

刚才是找里在数组里的元素的排名，如果找一个不在数组里的元素可不可以用 Leftmost，当然可以，各位看 Returns，它的返回值是不是应该为 >= 5 最靠左的索引，那最靠左的是不是 7，它的索引求出来应该是 5，所以 Leftmost(5) 求出来的结果就是 5，然后再加上 1 就是它的排名了，所以后面 5 添加进数组里，它的排名就是 6。

总结一下，以后求排名就可以用 Leftmost() + 1 这个公式。

再来看一下怎么求前任，求前任还是用 Leftmost，比如说我要求 4 的前任，那你肯定要找到最左侧的 4，然后最左侧的 4 再减去 1 就是最左侧的 4 的前任，所以公式应该是 Leftmost(4) - 1，求出来后就是 4 前面的 2。

再求一个数组里没有的 5，它的公式也是和上面的一样：Leftmost(5) - 1，它返回的是 >= 5 的最靠左的索引，是不是就是 7，减去 1 后就是 7 前面的 4。

所以，求前任的公式是：Leftmost(target) - 1

求后任就要用 Rightmost，还是找 4，先用 Rightmost 找到数组里最右侧的 4 的索引，然后再加上 1 就求出来它的后任了，所以它的公式各位想必也看出来了，就是：Rightmost(target) + 1

同样再看数组里没有的元素 5 的后任，把参数传如后就是 Rightmost(5) + 1，它要找的是 <= 5 的最靠右的索引，那是不是就是数组里最靠右的 4？再加 1 后同样也能找到旁边的 7。

做个小汇总，求前任：Leftmost(target) - 1，求后任：Rightmost(target) + 1。

求最近邻居就是先求出前任，再求出后任，然后在前后任里找一个更小的，就是 target 的最近邻居。

最后看这个范围查询，它就要找数组内所有 <，<=，>，>= target，按这种条件去进行查询就叫范围查询。

比方说我们现在想要查找所有小于 4 的元素，从上面的数组里就可以看到小于 4 的元素只有 1 和 2，假设我们的元素叫 x，要找小于 4 的就是 x < 4，这里显然是用 Leftmost，先找到最左侧的 4，然后再减 1，是不是就是它靠左侧这个元素了，但是我们要找到所有的该怎么办？很简单，因为数组的索引都是从 0 开始的，我们把这个范围设置为从 0 到 Leftmost(4) - 1就可以了，所以公式就是：0 到 Leftmost(target) - 1。

再看一个例子，这次我想要找 <= 4 的元素，注意这里是 <=，也就是说 1 和 2 后面几个元素也在查找的范围内，这里就要用0..Rightmost(4)，也就是从 0 一直到最右侧的 4.

看过了小于，小于等于，再看一个大于的，比如我要找所有大于 4 的元素，就是 x > 4，大于 4 的是不是 4 右边那些元素，同样我们先找到最右侧的 4，也就是Rightmost(4) + 1.. 从它作为起点一直到无穷大，这些范围就是 x > 4 的范围。

如果是大于等于 4 的呢？那就是把那几个4也要包含在内，所以这里要改成Leftmost(4)，找到最左侧的 4，然后以最左侧的 4 作为起点，一直向右到无穷大。

当然，这几个查询范围也是可以组合的，比如说我现在再要一个需求，我要找 4 <= x <= 7 的元素，那范围是不是从 4 的 Leftmost 开始到 7 的 Rightmost 结束，也就是Leftmost(4) .. Rightmost()7，这是包含边界的，包含等于的，现在我再改改，现在我要的是 4 < x < 7，大于 4 是不是 Rightmost(4) + 1，毕竟四总得往右找，然后一直到 Leftmost(7) - 1，因为 7 不能包含再内，所以是 7 往左找，这个就是一个简单的组合。