零基础-动手学深度学习-8.1 序列模型

原创已于 2025-07-30 03:35:07 修改 · 692 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #人工智能

于 2025-07-30 02:19:31 首次发布

零基础-李沐动手学深度学习-笔记专栏收录该内容

65 篇文章

订阅专栏

随着时间推移，人们对一件事的看法会发生很大的变化，心理学家对这些现象取了名字：

锚定（anchoring）效应：基于其他人的意见做出评价。
享乐适应（hedonic adaption）：人们迅速接受并且适应一种更好或者更坏的情况作为新的常态。例如，在看了很多好电影之后，人们会强烈期望下部电影会更好。因此，在许多精彩的电影被看过之后，即使是一部普通的也可能被认为是糟糕的。
季节性（seasonality）：少有观众喜欢在八月看圣诞老人的电影。
有时，电影会由于导演或演员在制作中的不当行为变得不受欢迎。
有些电影因为其极度糟糕只能成为小众电影。

简而言之，电影评分决不是固定不变的。因此，使用时间动力学可以得到更准确的电影推荐 (Koren, 2009)。当然，序列数据不仅仅是关于电影评分的。下面给出了更多的场景。

在使用程序时，许多用户都有很强的特定习惯。例如，在学生放学后社交媒体应用更受欢迎。在市场开放时股市交易软件更常用。
预测明天的股价要比过去的股价更困难，尽管两者都只是估计一个数字。毕竟，先见之明比事后诸葛亮难得多。在统计学中，前者（对超出已知观测范围进行预测）称为外推法（extrapolation），而后者（在现有观测值之间进行估计）称为内插法（interpolation）。
在本质上，音乐、语音、文本和视频都是连续的。如果它们的序列被我们重排，那么就会失去原有的意义。比如，一个文本标题“狗咬人”远没有“人咬狗”那么令人惊讶，尽管组成两句话的字完全相同。
地震具有很强的相关性，即大地震发生后，很可能会有几次小余震，这些余震的强度比非大地震后的余震要大得多。事实上，地震是时空相关的，即余震通常发生在很短的时间跨度和很近的距离内。
人类之间的互动也是连续的，这可以从微博上的争吵和辩论中看出。

8.1.1. 统计工具

处理序列数据需要统计工具和新的深度神经网络架构。

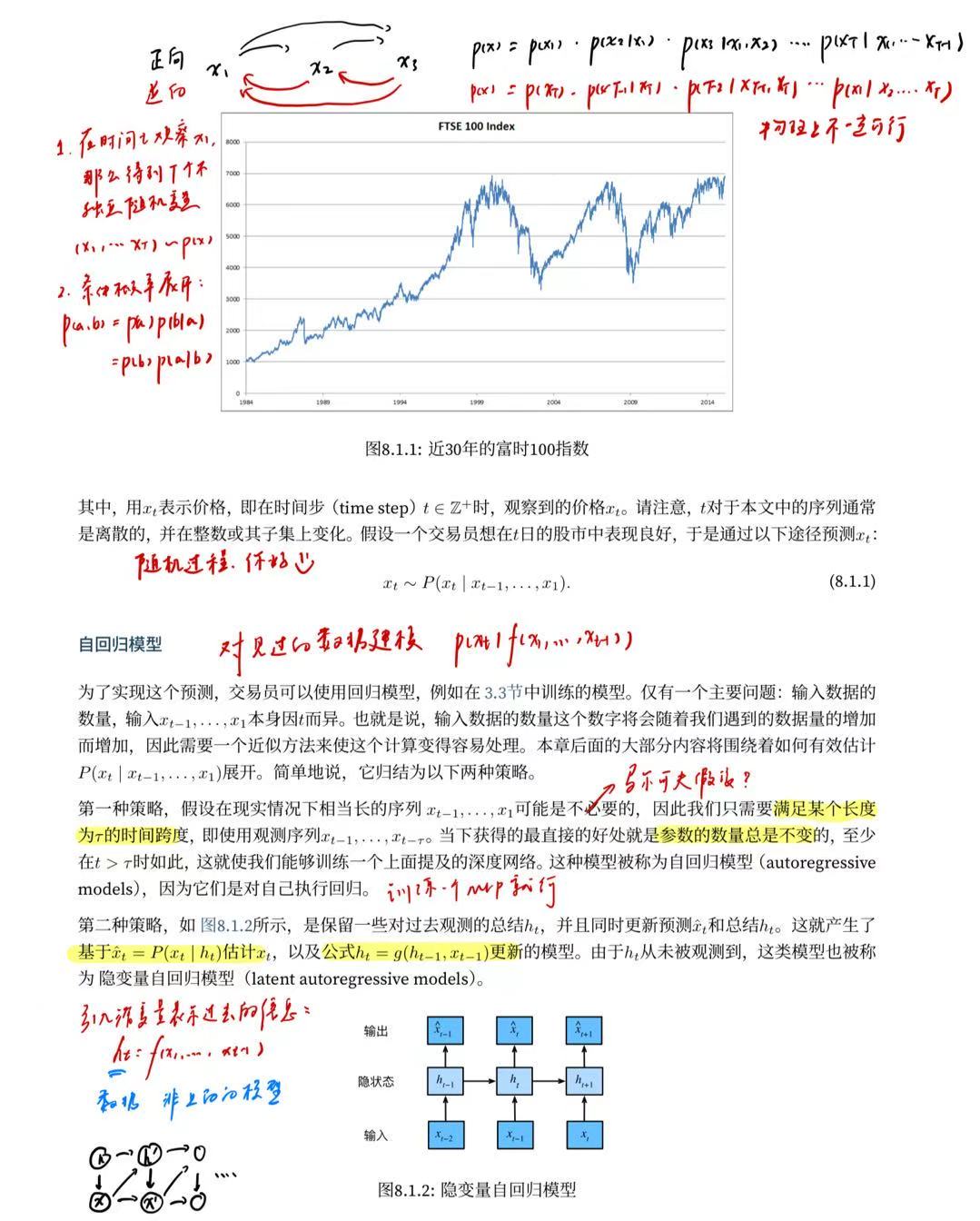
总的来说就是向前推进的方向恰好是我们感兴趣的方向

8.1.2. 训练

在了解了上述统计工具后，让我们在实践中尝试一下！首先，我们生成一些数据：使用正弦函数和一些可加性噪声来生成序列数据，时间步为1，2，....，1000

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

T = 1000  # 总共产生1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))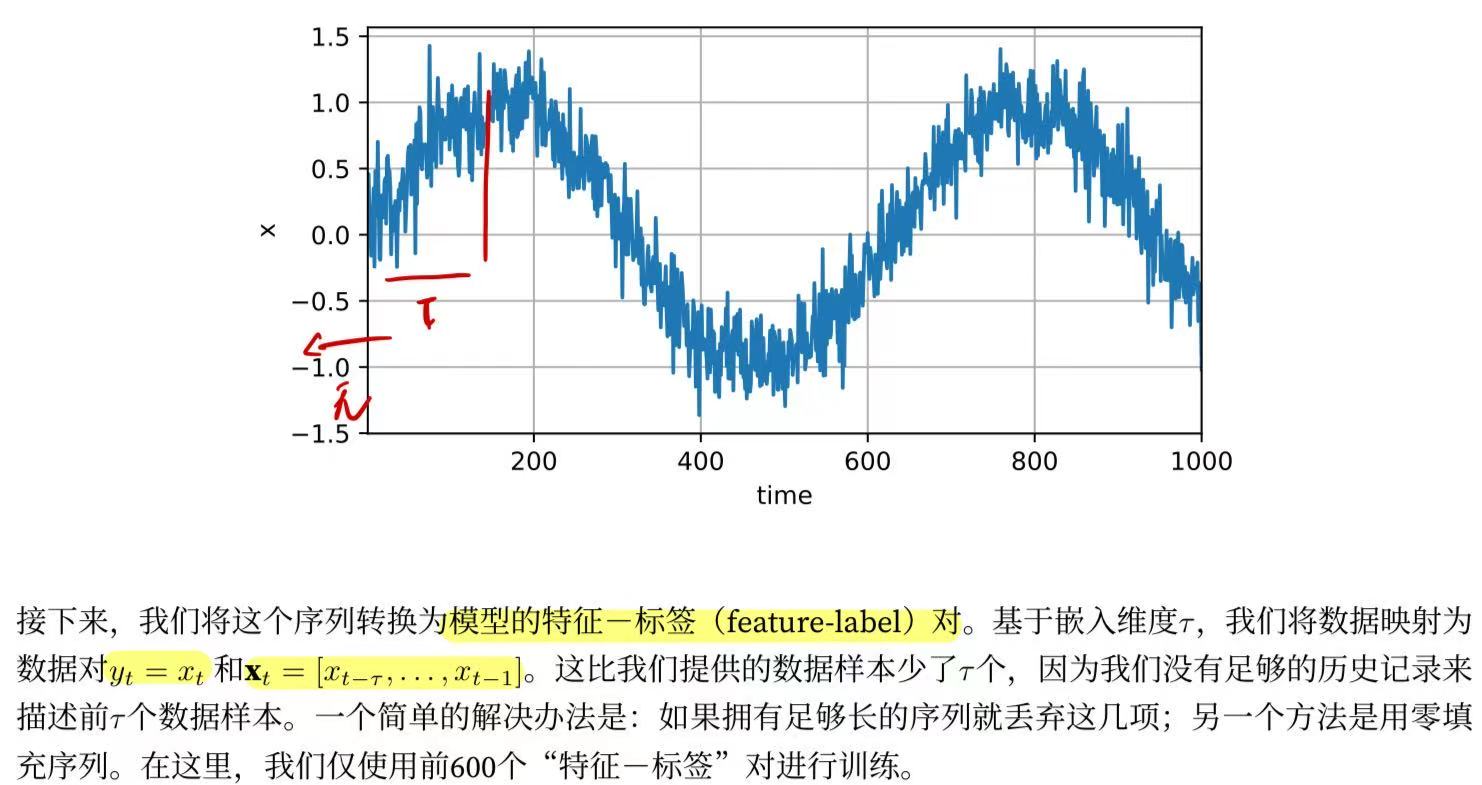

tau = 4 #这里历史记录为四项
features = torch.zeros((T - tau, tau))#这里是定义了一个有两个元素组成的元组？应该不是吧（样本数996，特征数4）
for i in range(tau):
    features[:, i] = x[i: T - tau + i]#每个特征对应的输入数据对

第 0 列：x[0], x[1], ..., x[T-tau-1]（即每个样本的第1个历史值）
第 1 列：x[1], x[2], ..., x[T-tau]（即每个样本的第2个历史值）
...
第 3 列：x[3], x[4], ..., x[T-1]（即每个样本的第4个历史值）
所以每行就是 x[t], x[t-1], x[t-2], x[t-3]，用于预测 x[t+1]


labels = x[tau:].reshape((-1, 1))#构造标签，即每个样本对应的“下一个值”

batch_size, n_train = 16, 600
# 只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
                            batch_size, is_train=True)

在这里，我们使用一个相当简单的架构训练模型：一个拥有两个全连接层的多层感知机，ReLU激活函数和平方损失：

# 初始化网络权重的函数
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)

# 一个简单的多层感知机
def get_net():
    net = nn.Sequential(nn.Linear(4, 10),
                        nn.ReLU(),
                        nn.Linear(10, 1))
    net.apply(init_weights)
    return net

# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')

现在，准备训练模型了。实现下面的训练代码的方式与前面几节（如 3.3节）中的循环训练基本相同。因此，我们不会深入探讨太多细节。

def train(net, train_iter, loss, epochs, lr):
    trainer = torch.optim.Adam(net.parameters(), lr)
    for epoch in range(epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.sum().backward()
            trainer.step()
        print(f'epoch {epoch + 1}, '
              f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')

net = get_net()
train(net, train_iter, loss, 5, 0.01)

输出：
epoch 1, loss: 0.076846
epoch 2, loss: 0.056340
epoch 3, loss: 0.053779
epoch 4, loss: 0.056320
epoch 5, loss: 0.051650

8.1.3. 预测

由于训练损失很小，因此我们期望模型能有很好的工作效果。让我们看看这在实践中意味着什么。首先是检查模型预测下一个时间步的能力，也就是单步预测（one-step-ahead prediction）。

onestep_preds = net(features)
d2l.plot([time, time[tau:]],
         [x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
         'x', legend=['data', '1-step preds'], xlim=[1, 1000],
         figsize=(6, 3))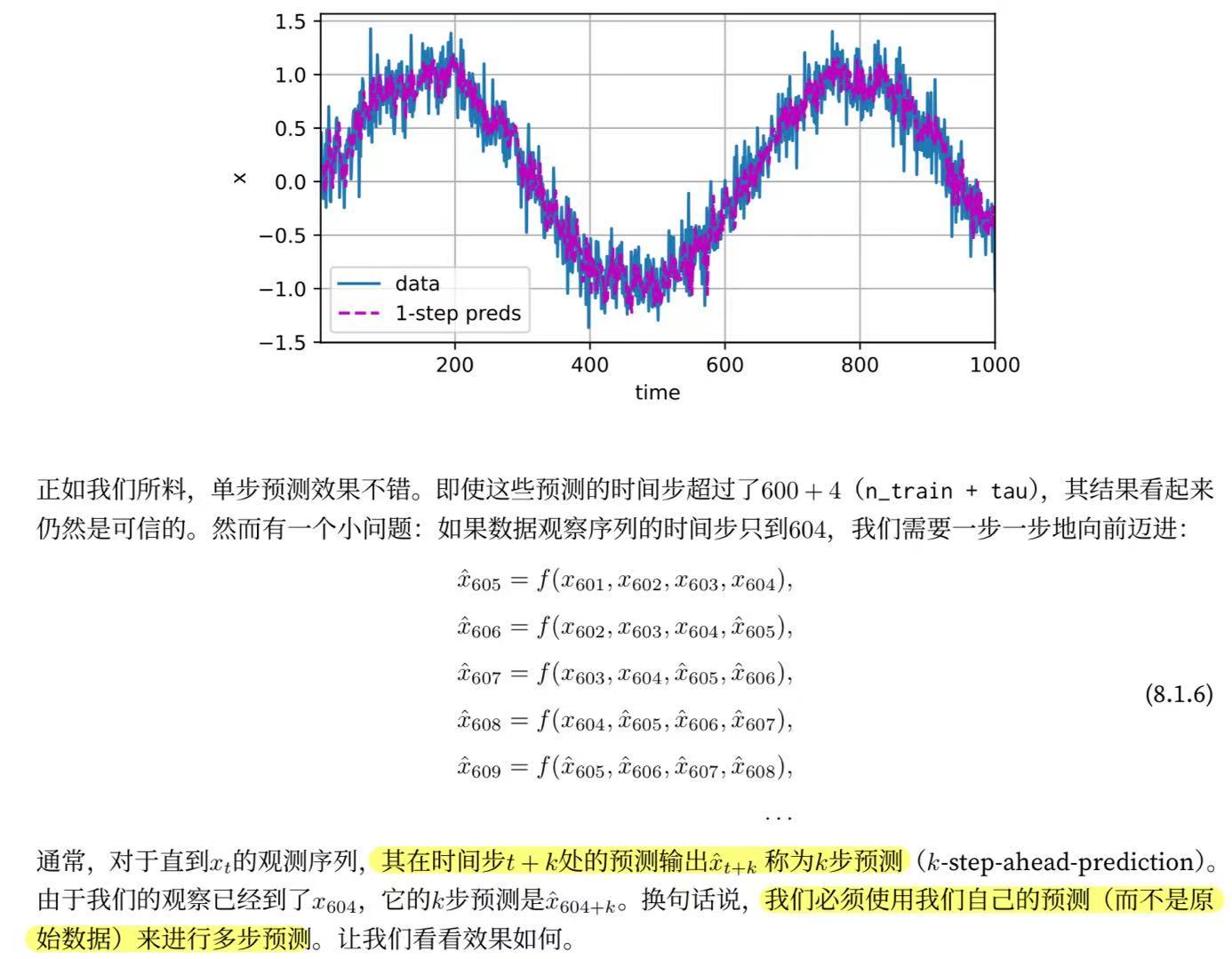

multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):
    multistep_preds[i] = net(
        multistep_preds[i - tau:i].reshape((1, -1)))#设定是从train之后的预测出来的输出

d2l.plot([time, time[tau:], time[n_train + tau:]],
         [x.detach().numpy(), onestep_preds.detach().numpy(),
          multistep_preds[n_train + tau:].detach().numpy()], 'time',
         'x', legend=['data', '1-step preds', 'multistep preds'],
         xlim=[1, 1000], figsize=(6, 3))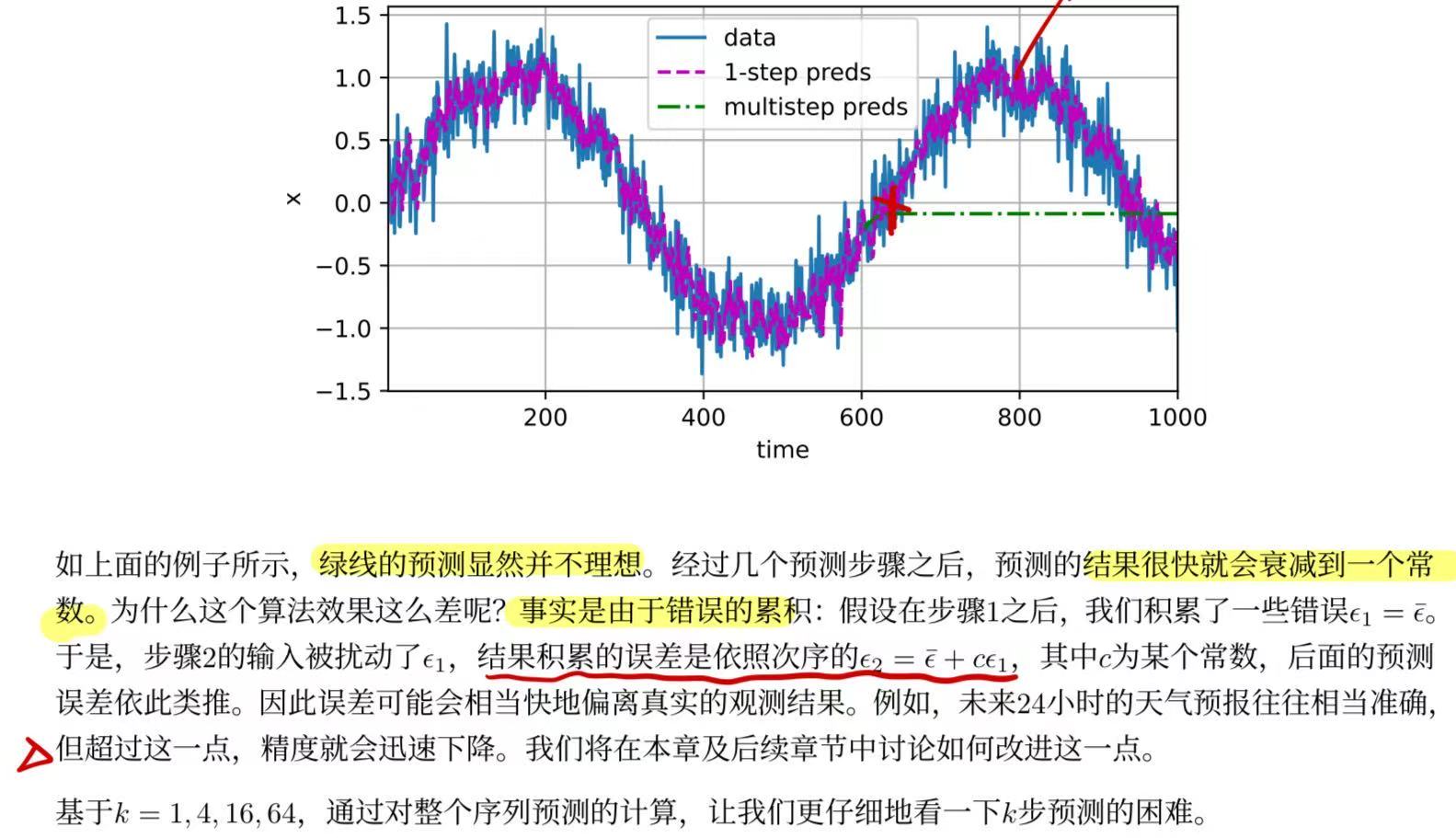

基于k=1,4,16,64，通过对整个序列预测的计算，让我们更仔细地看一下步预测的困难 :

max_steps = 64

features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
# 列i（i<tau）是来自x的观测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau):
    features[:, i] = x[i: i + T - tau - max_steps + 1]

# 列i（i>=tau）是来自（i-tau+1）步的预测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau, tau + max_steps):
    features[:, i] = net(features[:, i - tau:i]).reshape(-1)

steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
         [features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',
         legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
         figsize=(6, 3))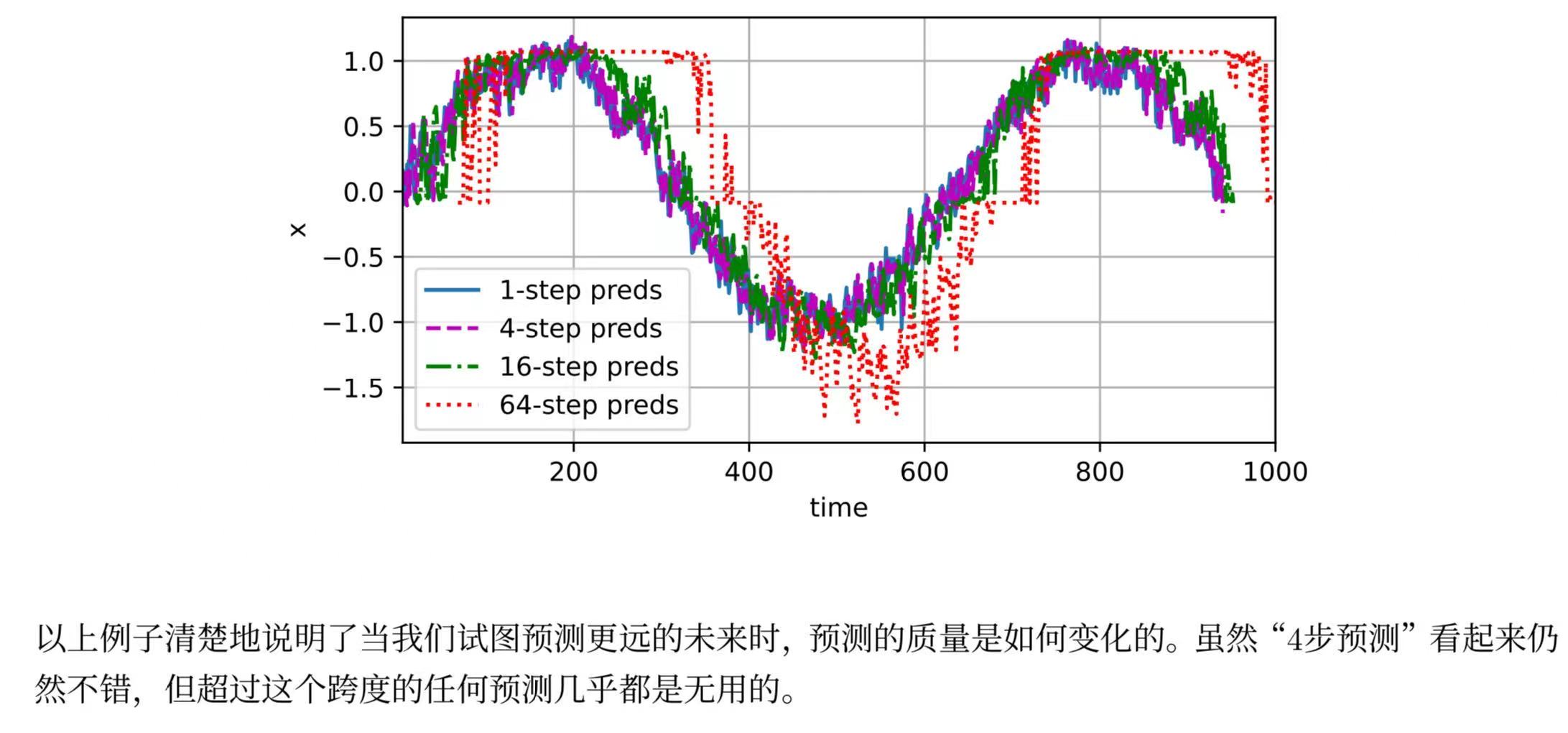

8.1.4. 小结

内插法（在现有观测值之间进行估计）和外推法（对超出已知观测范围进行预测）在实践的难度上差别很大。因此，对于所拥有的序列数据，在训练时始终要尊重其时间顺序，即最好不要基于未来的数据进行训练。
序列模型的估计需要专门的统计工具，两种较流行的选择是自回归模型和隐变量自回归模型。
对于时间是向前推进的因果模型，正向估计通常比反向估计更容易。
对于直到时间步t的观测序列，其在时间步t+k的预测输出是“步预测”。随着我们对预测时间值的增加，会造成误差的快速累积和预测质量的极速下降。