人工智能的物理根基：2024年诺贝尔物理学奖为何颁给AI先驱？

引言/导读

2024年10月8日，约翰·霍普菲尔德（John Hopfield）和杰弗里·辛顿（Jeffrey Hinton）因其对人工智能领域的贡献，荣获诺贝尔物理学奖。这一消息令许多人感到意外：为何计算科学和深度学习领域的奠基人会获得物理学的最高荣誉？答案隐藏在AI算法最底层的基本原理之中。

AI，从聊天机器人、图像生成器到黑洞照片增强和蛋白质结构预测，已经渗透到社会的方方面面。然而，我们常常忽略了这些算法与宇宙的基本规律——磁学、粒子物理学和量子场论之间存在的深刻且出人意料的联系。

本文将深入梳理并分析这一跨学科的视频内容，揭示人工智能从宏观的能量景观到微观的量子场波动所依赖的物理学框架，并探讨这种融合如何为理解AI“黑箱”提供钥匙，同时加速基础物理学的探索。

---

机器智能的物理起源：从磁性到记忆

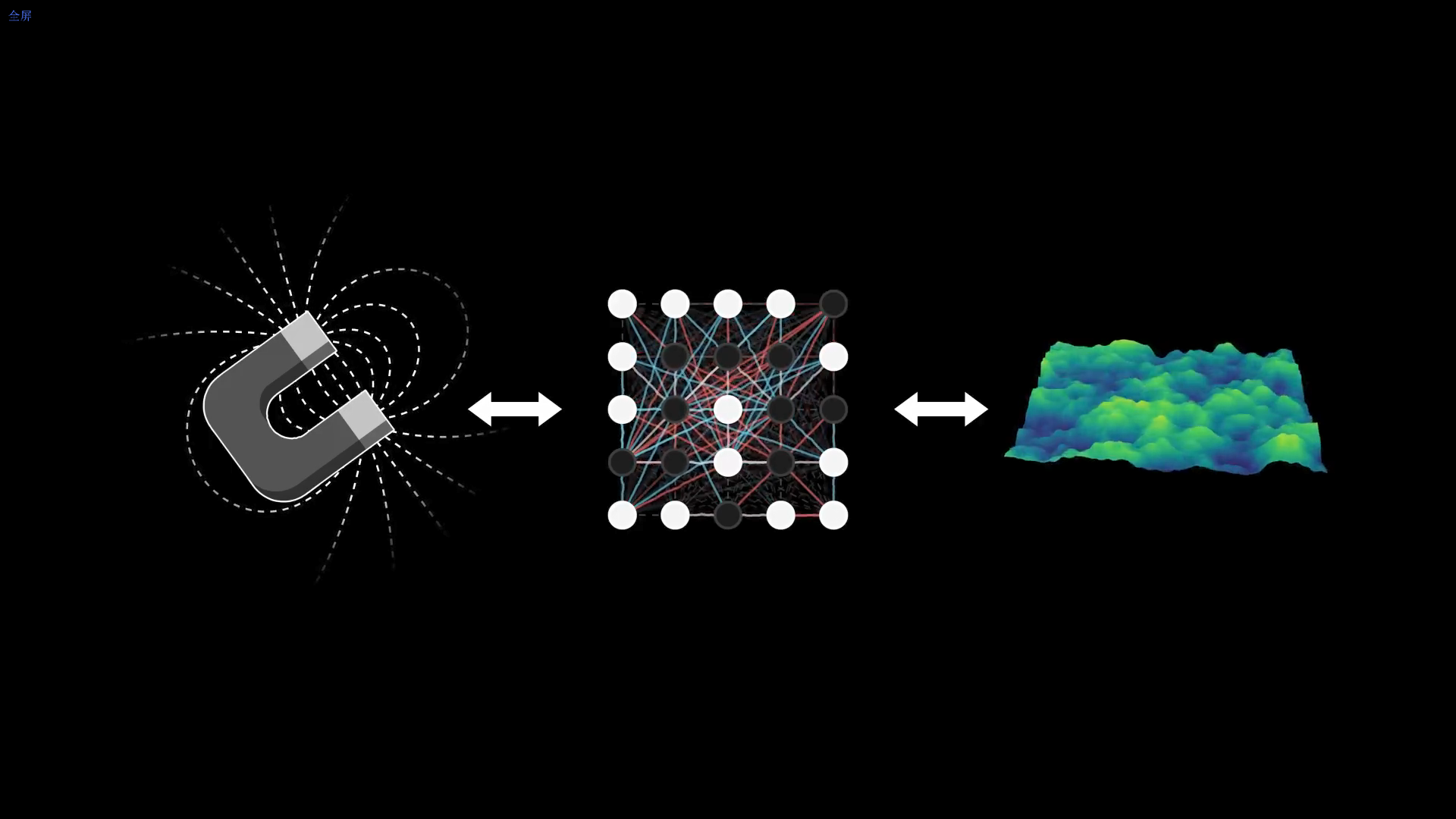
人工智能并非无源之水，它的神经网络模型直接汲取了凝聚态物理学中的经典概念。理解现代AI的基石，必须追溯到二十世纪初的磁学研究。

伊辛模型：万物趋于稳定的物理定律

1920年，德国物理学家威廉·楞次（Wilhelm Lenz）向他的学生恩斯特·伊辛（Ernst Ising）提出了一个问题：研究一个用于理解某些材料（如铁）磁性的模型。

• 结构与机制： 一块铁块由原子组成，电子的自旋（Spin）产生微小的磁场。自旋大致只有两种状态：上或下。伊辛将原子结构简化为一个网格，网格中的自旋会随时间演化。
• 能量与对齐： 周围环境的温度会导致自旋随机波动。但更重要的是，网格中相邻的自旋倾向于相互对齐，因为这种配置所需的能量更低，因此更加稳定。随着时间推移，磁域（相邻自旋对齐的区域）逐渐形成。如果施加外部磁场，所有自旋最终都会与该磁场对齐，使铁块转变为大规模磁体。伊辛模型成功地解释了铁磁性等现象。

为了更好地理解伊辛模型，我们可以将其想象成一颗在崎岖山脉景观中滚动的大理石。大理石的位置代表网格在特定时刻的配置，而其高度则代表与该配置相关的能量（即能量景观）。随着时间推移，大理石会滚向更低、更稳定的配置，如同自旋相互对齐，网格松弛一样。

霍普菲尔德网络：能量景观的雕塑家

时间快进到1982年，计算机科学蓬勃发展。美国科学家约翰·霍普菲尔德（John H. Hopfield）受到伊辛模型的启发，构建了一种能够记忆模式的新算法：霍普菲尔德网络。