Python数据结构(六):Python 基本排序算法:冒泡 选择 插入

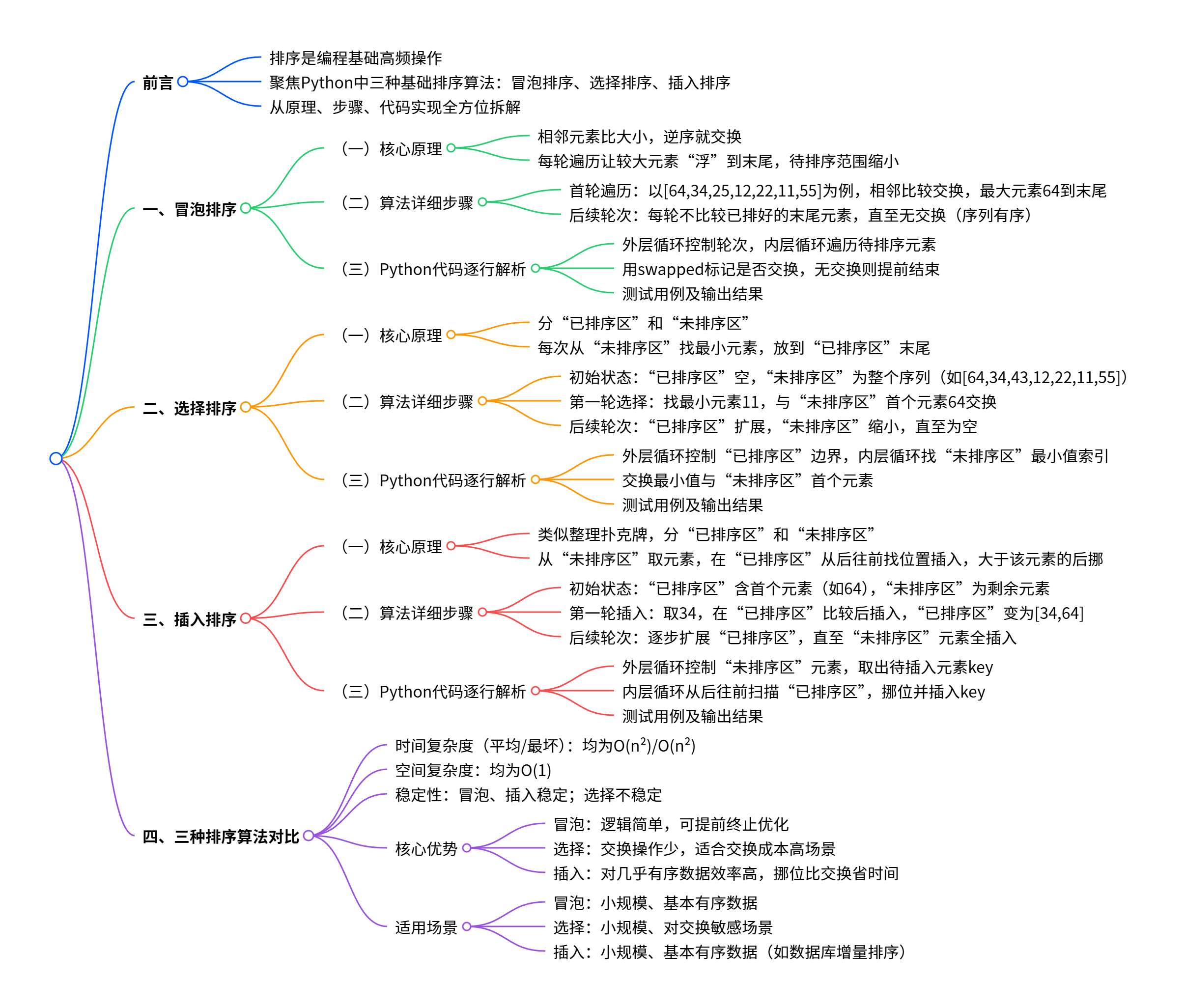
思维导图

前言

排序是编程领域最基础且高频的操作之一，小到处理简单的成绩排名，大到大规模数据的预处理，都离不开高效的排序逻辑。今天，我们就聚焦Python中的冒泡排序、选择排序和插入排序这三种基础算法，从原理、步骤到代码实现，全方位拆解，帮你彻底掌握它们的核心逻辑。

一、冒泡排序

（一）核心原理

冒泡排序的核心思路可以概括为“相邻元素比大小，逆序就交换”。想象一下，序列里的元素就像水中的泡泡，每一轮遍历中，较大的元素会像泡泡一样“浮”到序列的末尾。每完成一轮，待排序的范围就缩小一点，直到所有元素都有序排列。

（二）算法详细步骤

1. 首轮遍历（以序列[64, 34, 25, 12, 22, 11, 55]为例）：
   • 从序列起始位置开始，比较第1个和第2个元素（64和34），因为64 > 34，所以交换位置，序列变为[34, 64, 25, 12, 22, 11, 55]；
   • 接着比较第2个和第3个元素（64和25），64 > 25，交换后序列是[34, 25, 64, 12, 22, 11, 55]；
   • 依此类推，每一次比较相邻元素，逆序就交换。首轮结束后，最大的元素64会“浮”到序列末尾，此时序列变为[34, 25, 12, 22, 11, 55, 64]。
2. 后续轮次：
   • 第二轮遍历不再比较最后一个元素（已确定是最大的），重复“相邻比较、逆序交换”的过程，次大的元素55会浮到倒数第二的位置；
   • 每一轮遍历后，待排序的元素数量减1，直到某一轮遍历中没有任何元素交换（说明序列已完全有序），排序结束。

（三）Python代码逐行解析

def bubble_sort(arr):
    n = len(arr)  # 获取序列长度，用于控制遍历轮次
    for i in range(n):  # 外层循环：控制排序的轮次，共n轮
        # 标记本轮是否发生交换，若为False，说明序列已有序，可提前结束
        swapped = False  
        # 内层循环：每轮遍历待排序的元素（每轮结束后，末尾已排好的元素不再比较）
        for j in range(0, n - i - 1):  
            if arr[j] > arr[j + 1]:  # 若前元素大于后元素，发生逆序
                arr[j], arr[j + 1] = arr[j + 1], arr[j]  # 交换相邻元素
                swapped = True  # 标记本轮发生了交换
        if not swapped:  # 若本轮无交换，直接退出循环，排序完成
            break
    return arr

# 测试用例
test_arr = [64, 34, 25, 12, 22, 11, 55]
sorted_arr = bubble_sort(test_arr)
print("冒泡排序结果：", sorted_arr)  # 输出：[11, 12, 22, 25, 34, 55, 64]

二、选择排序

（一）核心原理

选择排序的逻辑十分直接：把序列分成**“已排序区”和“未排序区”**。每次从“未排序区”中找出最小（或最大）的元素，放到“已排序区”的末尾。重复这个过程，直到“未排序区”为空，整个序列就有序了。

（二）算法详细步骤

1. 初始状态：“已排序区”为空，“未排序区”是整个序列（如[64, 34, 43, 12, 22, 11, 55]）。
2. 第一轮选择：
   • 在“未排序区”中遍历，找到最小的元素11，记录其索引；
   • 将11与“未排序区”的第一个元素64交换，此时“已排序区”为[11]，“未排序区”变为[34, 43, 12, 22, 64, 55]。
3. 后续轮次：
   • 第二轮在“未排序区”中找最小元素12，与“未排序区”第一个元素34交换，“已排序区”变为[11, 12]；
   • 每轮结束后，“已排序区”长度加1，“未排序区”长度减1，直到“未排序区”为空。

（三）Python代码逐行解析

def selection_sort(arr):
    n = len(arr)  # 获取序列长度
    for i in range(n):  # 外层循环：控制“已排序区”的边界，共n轮
        min_idx = i  # 假设“未排序区”第一个元素是最小值，记录其索引
        # 内层循环：遍历“未排序区”，寻找真正的最小值索引
        for j in range(i + 1, n):  
            if arr[j] < arr[min_idx]:  # 若找到更小的元素
                min_idx = j  # 更新最小值的索引
        # 交换“未排序区”第一个元素与最小值
        arr[i], arr[min_idx] = arr[min_idx], arr[i]  
    return arr

# 测试用例
test_arr = [64, 34, 43, 12, 22, 11, 55]
sorted_arr = selection_sort(test_arr)
print("选择排序结果：", sorted_arr)  # 输出：[11, 12, 22, 34, 43, 55, 64]

三、插入排序

（一）核心原理

插入排序的逻辑很像我们整理扑克牌：把序列分为“已排序区”和“未排序区”，每次从“未排序区”取一个元素，在“已排序区”中从后往前找位置，找到后插入，同时把“已排序区”中大于该元素的部分向后挪位。

（二）算法详细步骤

1. 初始状态：“已排序区”只有序列的第一个元素（如64），“未排序区”是剩下的元素（[34, 43, 12, 22, 11, 55]）。
2. 第一轮插入：
   • 取“未排序区”的第一个元素34作为“待插入元素”；
   • 在“已排序区”（只有64）中比较，34 < 64，所以64向后挪位，将34插入到“已排序区”开头，此时“已排序区”为[34, 64]，“未排序区”变为[43, 12, 22, 11, 55]。
3. 后续轮次：
   • 第二轮取“未排序区”的43，在“已排序区”[34, 64]中从后往前比较，43 < 64，64后挪，43插入到34和64之间，“已排序区”变为[34, 43, 64]；
   • 每轮插入后，“已排序区”逐步扩展，直到“未排序区”元素全部插入。

（三）Python代码逐行解析

def insertion_sort(arr):
    n = len(arr)  # 获取序列长度
    # 外层循环：控制“未排序区”的元素（从第二个元素开始，索引为1）
    for i in range(1, n):  
        key = arr[i]  # 取出“待插入元素”
        j = i - 1  # “已排序区”的最后一个元素索引
        # 内层循环：从后往前扫描“已排序区”，挪位并找插入位置
        while j >= 0 and key < arr[j]:  
            arr[j + 1] = arr[j]  # 若“已排序区”元素大于待插入元素，向后挪位
            j -= 1  # 继续向前比较
        arr[j + 1] = key  # 将待插入元素放到找到的位置
    return arr

# 测试用例
test_arr = [64, 34, 43, 12, 22, 11, 55]
sorted_arr = insertion_sort(test_arr)
print("插入排序结果：", sorted_arr)  # 输出：[11, 12, 22, 34, 43, 55, 64]

四、三种排序算法对比

为了更清晰地对比三者的差异，我们从时间复杂度（算法执行时间随数据规模增长的趋势）、空间复杂度（算法占用内存的大小）、稳定性（相同元素排序后相对位置是否不变）、核心优势和适用场景五个维度分析：

排序算法	时间复杂度（平均/最坏）	空间复杂度	稳定性	核心优势	适用场景
冒泡排序	( O(n^2) ) / ( O(n^2) )	( O(1) )	稳定	逻辑最简单，代码极易实现；若数据已接近有序，可通过“提前终止”优化效率（如代码中swapped标记）	小规模数据排序；数据基本有序的场景（如仅少数元素位置错误）
选择排序	( O(n^2) ) / ( O(n^2) )	( O(1) )	不稳定	交换操作极少（仅需( n-1 )次交换），对“交换成本高”的场景友好（如元素是复杂对象，交换耗时）	数据量小，且对“交换操作”性能敏感的场景；或希望减少交换次数的场景
插入排序	( O(n^2) ) / ( O(n^2) )	( O(1) )	稳定	对“几乎有序”的数据效率极高（接近( O(n) )）；“挪位”操作比“交换”更节省时间（只需赋值，无需临时变量）	小规模数据排序；数据基本有序的场景（如数据库增量数据排序）