基于Huffman编码的文件压缩

原理剖析：

我们的Huffman文件压缩，是基于Huffman编码实现的，思路如下：
首先，获取原文件中每个字节的值(unsigned char)类型，范围为0-255，并记录每个值出现的次数，以这些值出现的次数为数据，利用贪心算法构建Huffman编码，然后，将对应的字节以其对应的Huffman编码替换达到压缩文件的目的。当然，为了能更好的解压缩我们需要将相应的字节与它们出现的次数也存储在压缩文件的开头处，以便我们在解压缩时通过这些数据来构建与压缩时相同的Huffman编码，并通过对应的替换来达到解压缩文件的目的。由于我们在利用贪心算法构建Huufman编码时，每次需要拿到数据中最小的两个次数，所以我们需要将这些数据以小堆的形式存储起来，每次拿取堆顶位置的数据便是最小的数据。所以我们需要说说下面的大小堆问题，以及后面的Huffman编码问题。

大小堆问题 ：

我们的堆底层是用vector来存储数据的，通过将vector虚拟成一颗完全二叉树的结构（方法见下）并通过调整完全二叉树中节点（方法如下）来满足我们堆的特性要求。堆有大堆和小堆之分，所谓小堆便是根节点的元素是这颗树中所有元素中最小的元素，并且其左右孩子也是其左右子树中值最小的元素，以此类推便是小堆，大堆也类似，不过根是所有元素中之最大的那个元素，左右孩子也是左右子树中最大的元素。
将vector虚拟成一颗完全二叉树的方法如下：
通过将vector从0开始的下标依次对应为完全二叉树层序遍历的各节点，例如：vector的0号下标元素当作是完全二叉树的根，将1号下标元素当作左孩子，2号下标元素当作右孩子 。。。
调节完全二叉树节点的方法如下：
构建时，从尾节点的父亲节点开始依照层序便利的顺序向根节点方向调用向下调整算法（_AdjustDown详细说明见代码处）调节每一颗子树，调节完根节点后，此完全二叉树便是相应的堆结构。
pop()时，我们是将堆顶元素与堆尾元素交换，然后删除堆尾元素（原来的堆顶元素），从现在的堆顶元素处调用一次向下调整算法（_AdjustDown详细说明见代码处），调节完成后整棵完全二叉树便又是相应的堆结构。
push时，我们将新元素插入到完全二叉树的最末尾，采用向上调整算法（_AdjustUp详细说明见代码处）从插入元素处调节完全二叉树，调节完成后此颗完全二叉树便又是相应的堆结构。
代码如下：

#pragma once
#include<iostream>
#include<vector>
#include<assert.h>
using namespace std;

//在调整算法中，比较两个元素的方法不同，分别对应构建不同的大小堆，
//下面为构建小堆的比较方法
template<class T>
struct SmallHeap{
    bool operator()(const T& left,const T& right){
        return left < right;
    }
};

//此处为构建大堆的比较方法
template<class T>
struct BigHeap{
    bool operator()(const T& left, const T& right){
        return left > right;
    }
};
//在实际应用时，根据传入的模板类型参数不同，构建不同的对象，采用仿函数的形式进行比较，提高代码复用


//默认为大堆
template<class T,class Compare = BigHeap<T>>
class Heap{
public:
    Heap()
    {}
    Heap(const T* arr,size_t n){
        if (arr && n){
            _heap.reserve(n);
            for (size_t i = 0; i < n; i++){
                _heap.push_back(arr[i]);
            }
            //从尾节点的父亲开始，以层序遍历的次序向根节点方向，依次采用向下调整算法
            for (int i = (n-2)/2; i >= 0; i--){
                _AdjustDown(i);
            }
        }
    }
    void Push(const T& x){
        _heap.push_back(x);
        //在插入节点处调用向上调整算法
        _AdjustUp(_heap.size() - 1);
    }
    void Pop(){
        assert(!_heap.empty());
        //交换堆顶、堆尾元素
        swap(_heap[0], _heap[_heap.size() - 1]);
        _heap.pop_back();
        //从堆顶处调用向下调整算法
        _AdjustDown(0);
    }
    const T& Top(){
        return _heap[0];
    }
    size_t Size(){
        return _heap.size();
    }
private:
    //向上调整算法
    void _AdjustUp(int child){
        assert(child < (int)_heap.size());
        //计算父亲节点在vector中的下标
        int parents = (child - 1) / 2;
        Compare com;
        //一直向上调整，直至调节完根节点或者进入else逻辑后才停止调节
        while (child > 0){
            //若为小堆的话，child小于parents为真
            if (com(_heap[child], _heap[parents])){
                swap(_heap[child], _heap[parents]);
                //计算新的child与parents
                child = parents;
                parents = (child - 1) / 2;//child * 2 + 1;
            }
            else{
                break;
            }
        }
    }
    //向下调整算法，此算法的前提是调节的该节点的左右子树已是相应的堆结构
    void _AdjustDown(int parents){
        //计算左孩子的下标
        int child = parents * 2 + 1;
        Compare com;
        while (child < (int)_heap.size()){
            if ((child + 1) < (int)_heap.size() && com(_heap[child + 1], _heap[child])){
                child++;
            }
            //比较左右孩子中最大或最小的孩子与父亲节点的大小，依据所要建立的大小堆不同
            //此处比较方法不同，例如要建立小堆的话，此处最小孩子小于父节点条件应为真
            if (com(_heap[child] , _heap[parents])){
                swap(_heap[child], _heap[parents]);
                parents = child;
                child = parents * 2 + 1;
            }
            else{
                break;
            }
        }
    }
protected:
    vector<T> _heap;
};

Huffman编码问题：

构建Huffman编码时，我们是利用上一步建立好的小堆来构建Huffman编码的，构建过程如下：
每次取堆中次数最小的两个节点，并将这两个节点出堆，以这两个节点出现的次数之和构建父节点，并将父节点与两个孩子节点连接起来，最后将父节点入堆，重复以上过程，直至堆中只有一个节点，此节点便为Huffman树的根节点。
代码如下：

#pragma once
#include"Heap.h"

//Huffman树节点
template<class T>
struct HuffmanTreeNode{
    HuffmanTreeNode<T>* _left;
    HuffmanTreeNode<T>* _right;
    HuffmanTreeNode<T>* _parents;

    T _t;
    HuffmanTreeNode(const T& t)
        :_t(t)
        , _left(NULL)
        , _right(NULL)
        , _parents(NULL)
    {}

};

//Huffman树
template<class T>
class HuffmanTree{
    typedef HuffmanTreeNode<T> Node;
public:
    HuffmanTree()
        :_root(NULL)
    {}
    //构建Huffman树
    HuffmanTree(T* t, size_t n, const T& invalid)//const T& invalid
    {
        //文件压缩需要构建小堆，小堆的比较方法
        struct NodeCompare{
            bool operator()(Node* left,Node* right){
                return left->_t < right->_t;

            }
        };
        assert(t && n);
        Heap<Node*, NodeCompare> _heap;
        //将元素插入堆中
        for (size_t i = 0; i < n; i++){
            if (t[i] != invalid){
                _heap.Push(new Node(t[i]));
            }
            //_heap.Push(new Node(t[i]));
        }

        Node* left = NULL;
        Node* right = NULL;
        Node* parents = NULL;
        //调节成小堆
        while (_heap.Size() > 1){
            //将此次所有元素中两个最小元素出堆
            left = _heap.Top();
            _heap.Pop();
            right = _heap.Top();
            _heap.Pop();
            //构建此次所有元素中最小的两个元素出现次数之和，并将此次数插入小堆中
            parents = new Node(left->_t + right->_t);
            parents->_left = left;
            parents->_right = right;
            left->_parents = parents;
            right->_parents = parents;
            _heap.Push(parents);
        }
        _root = _heap.Top();
    }
    ~HuffmanTree(){
        if (_root){
            Distory(_root);
            _root = NULL;
        }
    }
    void Distory(Node* root){
        if (root == NULL){
            return;
        }
        Distory(root->_left);
        Distory(root->_right);
        delete root;
    }
    Node* GetRoot(){
        return _root;
    }
private:
    //防拷贝
    HuffmanTree(const HuffmanTree<T>& t);
    HuffmanTree<T>& operator=(const HuffmanTree<T>& t);
protected:
    Node* _root;
};

---

文件压缩：

压缩与解压缩流程如下：
压缩：读原文件->构建小堆->构建Huffman编码->压缩->产生压缩文件
解压缩：读压缩文件->构建小堆->构建Huffman编码->解压缩->产生解压缩文件
代码：

#define _CRT_SECURE_NO_WARNINGS 1

#pragma once
#include"HuffmanTree.h"
#include<string>
#include<stdio.h>
#include<assert.h>

//存储字符与字符出现次数的结构
struct CharInfo{
    char _char; //字符
    long long _count;   //字符出现次数
    string _code;   //此字符对应的Huffman编码
    //两个节点出现次数相加
    CharInfo operator+(const CharInfo& ch){
        CharInfo tmp;
        tmp._count = _count + ch._count;
        return tmp;
    }

    bool operator<(const CharInfo& ch){
        return _count < ch._count;
    }
    bool operator!=(const CharInfo& ch){
        return _count != ch._count;
    }
};


class FileCompress{
    typedef HuffmanTreeNode<CharInfo> Node;
public:
    //初始化，使256个元素每个元素对应一种字符
    FileCompress()
    {
        for (int i = 0; i < 256; ++i){
            _infos[i]._char = i;
            _infos[i]._count = 0;
        }
    }

    //压缩
    void Compress(const char* file){

        assert(file);
        FILE* fin = fopen(file, "rb");
        assert(fin);
        //统计各字符出现的次数
        int ret = 0;
        while ((ret = fgetc(fin)) != EOF){
            _infos[ret]._count++;
        }
        //构建Huffman树，过滤掉没出现的字符
        CharInfo invalid;   
        invalid._count = 0; //没出现的字符次数为0
        HuffmanTree<CharInfo> tree(_infos, 256, invalid);
        //总字符数
        long long sumchars = tree.GetRoot()->_t._count;

        //构建Huffman编码
        _GetHuffmanCode(tree.GetRoot(), "");
        string tmpstr(file);
        FILE* fout = NULL;

        //构建压缩文件名
        if (!fseek(fin, 0, SEEK_SET)){
            //size_t pos = tmpstr.rfind(".");
            //tmpstr.erase(pos, tmpstr.size() - pos);
            tmpstr += ".zip";
            //创建压缩文件，以二进制写的方式
            fout = fopen(tmpstr.c_str(), "wb");
            assert(fout);
        }
        else{
            assert(NULL);
        }

        //将各字符与对应的出现次数存储在压缩文件头部（包括没出现字符）
        for (size_t i = 0; i < 256; i++){
            fprintf(fout, "%lld ", _infos[i]._count);
        }

        long long nowsum = 0;
        static int tmp = 0;
        //压缩
        while (nowsum < sumchars){
            int ch = fgetc(fin);//(unsigned char)
            nowsum++;
            string ret = _infos[ch]._code;

            static int count = 0;
            size_t index = 0;
            //将每一个字符用相应的编码替换
            while (index < ret.size()){

                if (ret[index] == '0'){
                    tmp &= ~(1 << (count++));
                }
                else{
                    tmp |= (1 << (count++));
                }
                if (count == 8){
                    int ert = fputc(tmp, fout);
                    //fflush(fout);
                    tmp = 0;
                    count = 0;
                }
                index++;
            }
        }
        fputc(tmp, fout);
        fclose(fin);
        fclose(fout);
    }


    //左孩子加0，右孩子加1
    void _GetHuffmanCode(Node* root, string code){
        if (root == NULL){
            return;
        }
        if (root->_left == NULL && root->_right == NULL){

            _infos[(unsigned char)((root->_t)._char)]._code = code;
            return;
        }
        _GetHuffmanCode(root->_left, code + "0");
        _GetHuffmanCode(root->_right, code + "1");
    }



    //解压缩
    void UnCompress(const char* file){
        //初始化
        for (int i = 0; i < 256; ++i){
            _infos[i]._char = i;
            _infos[i]._count = 0;
        }
        //以二进制读的方式打开压缩文件
        assert(file);
        FILE* fin = fopen(file,"rb");
        if (fin == NULL) {
            perror("fopen");
            exit(1);
        }
        assert(fin);

        //读取压缩文件头部存储的原文件各字符与对应出现的次数
        for (size_t i = 0; i < 256; i++){
            fscanf(fin, "%lld ", &(_infos[i]._count));
        }

        CharInfo invalid;
        invalid._count = 0;
        //构建与原文件构建出的相同的Huffman树
        HuffmanTree<CharInfo> tree(_infos, 256, invalid);
        //总次数
        long long sumchars = ((tree.GetRoot())->_t)._count;

        //构建解压缩文件名
        string tmp(file);
        size_t pos = tmp.rfind("z");
        tmp.erase(pos, tmp.size() - pos);
        pos = tmp.rfind(".");
        tmp.erase(pos, tmp.size() - pos);

        tmp += "解压缩.txt";
        //以二进制写的方式创建解压缩文件
        FILE* fout = fopen(tmp.c_str(),"wb");

        Node* ret = tree.GetRoot();
        static Node* cur = ret;
        long long count = 0;
        //解压缩
        while (count < sumchars){
            int ch = fgetc(fin);


            int index = 0;
            while (index < 8){
                //如果走到叶子节点，用相应编码进行反向替换
                if (cur->_left == NULL && cur->_right == NULL){
                    int chr = cur->_t._char;
                    fputc(chr, fout);
                    //printf("%d", fputc(chr, fout));
                    count++;
                    cur = ret;
                    if (count == sumchars)
                        break;
                }//如果此位为1，则向Huffman树的右边寻找
                if (ch & (1 << index)){
                    cur = cur->_right;
                }
                else{//如果此位为0，则向Huffman树的左边寻找
                    cur = cur->_left;   
                }

                index++;
            }
        }

        fclose(fin);
        fclose(fout);
    }
private:
    CharInfo _infos[256];
};

void TestFileCompress(){
    FileCompress fc;
    fc.Compress("test.txt");
    printf("压缩成功！\n");
}
void TestFileUnCompress(){
    FileCompress fc;
    fc.UnCompress("test.txt.zip");
    printf("解压缩成功！\n");
}

mani.cpp

#pragma once
#include"Filecompress.h"

int main(){
    //TestFileCompress();
    TestFileUnCompress();
    return 0;
}

成果总结：

压缩前：

压缩后：

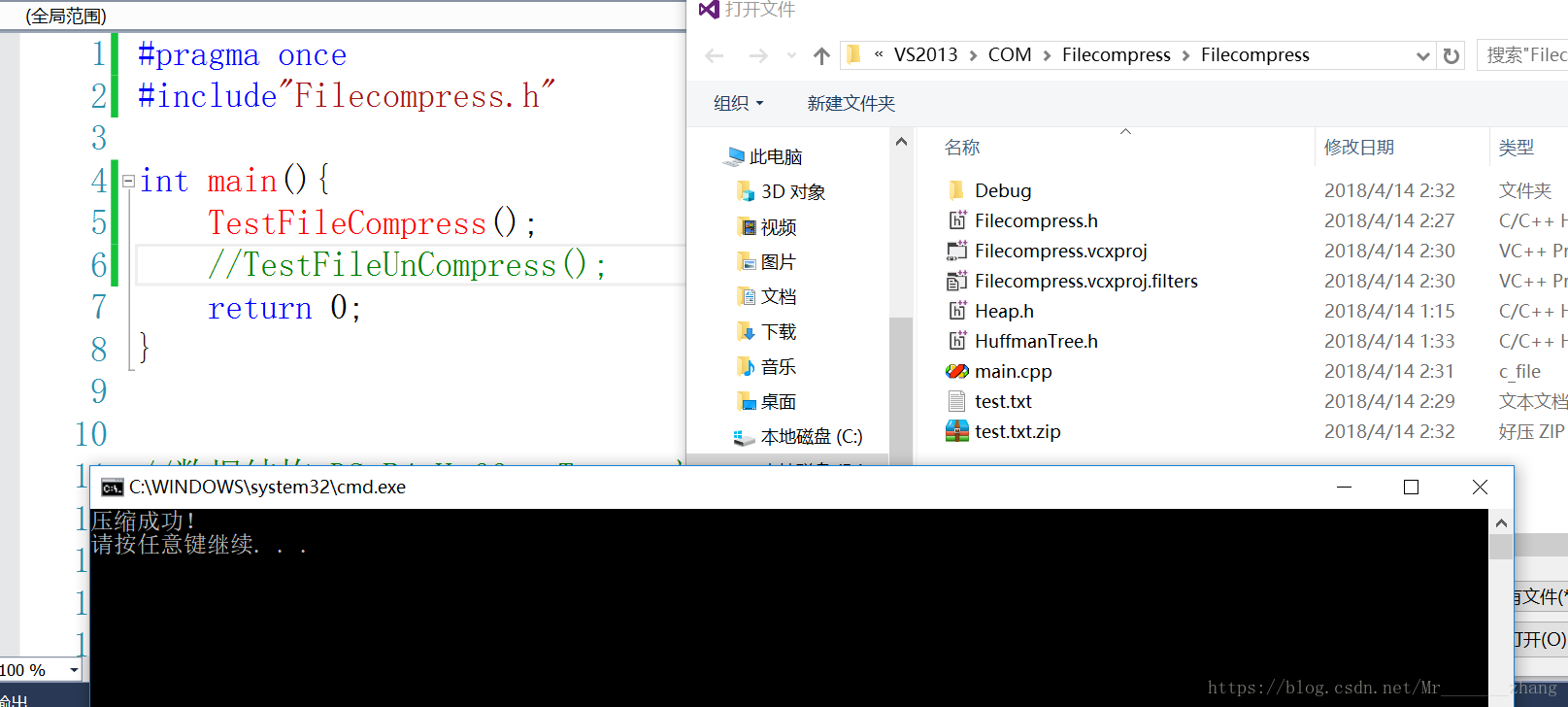
解压缩后：

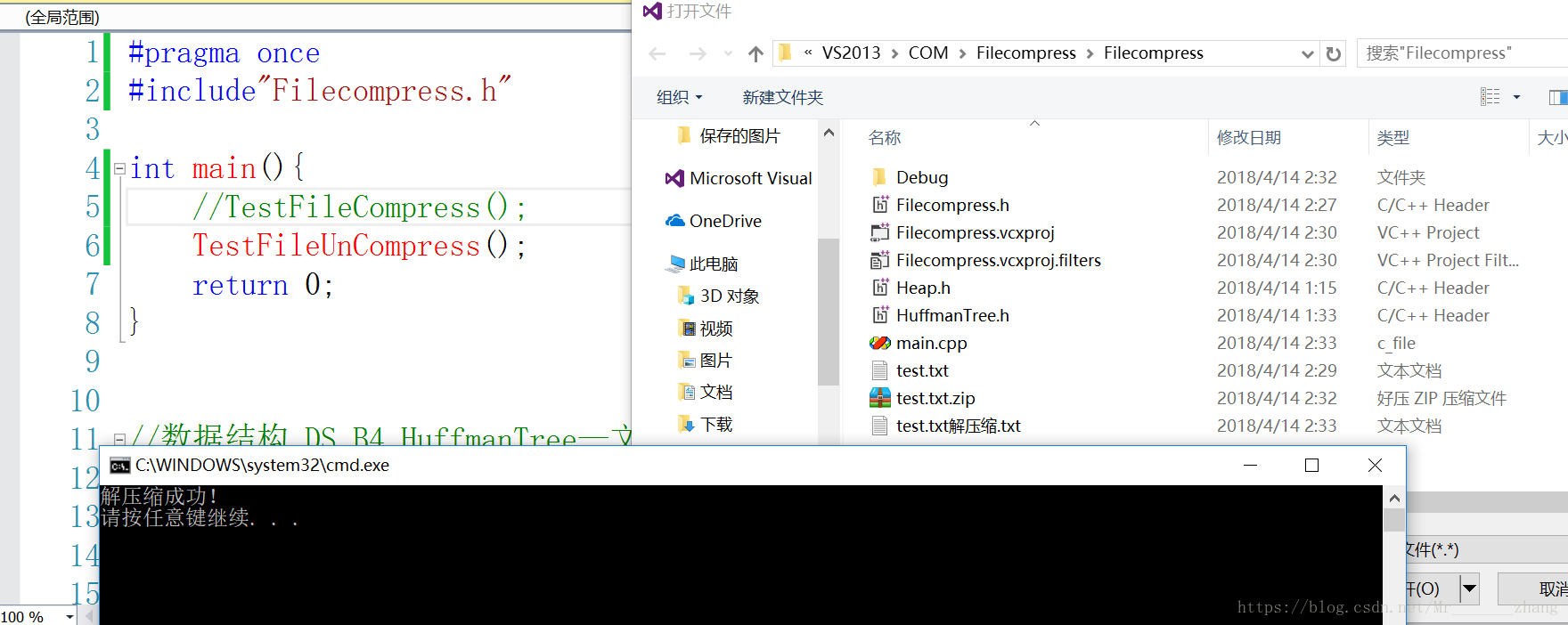
UC文件对比：

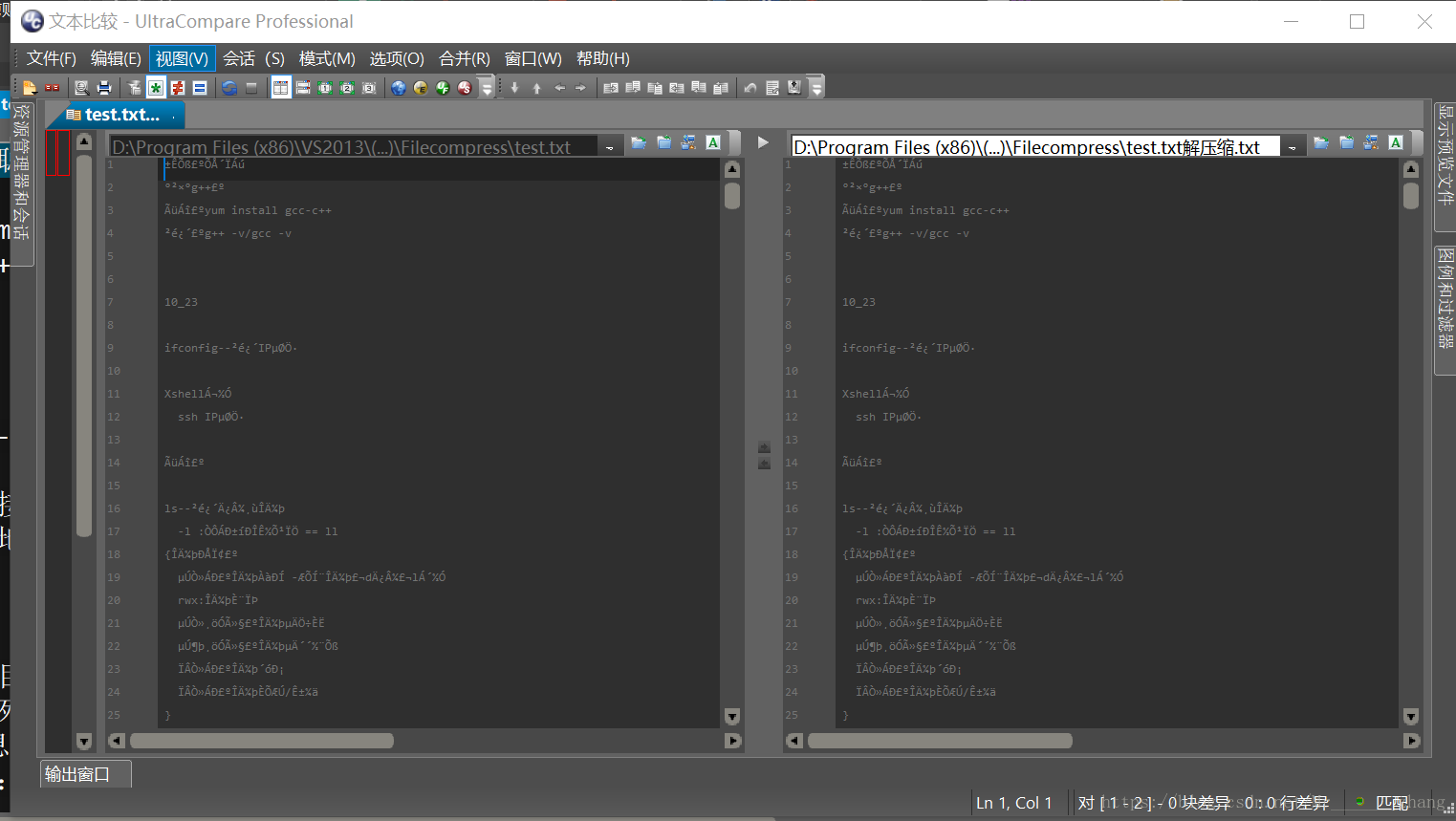
至此，我们的文件压缩与解压缩已经全部讲完，要说明的一点是，原文件各字符出现次数越松散文件压缩效率越高。