马尔可夫随机场 MRF 个人理解

最新推荐文章于 2024-04-26 16:41:39 发布

勝ち取った

最新推荐文章于 2024-04-26 16:41:39 发布

阅读量2k

点赞数

本文介绍了马尔可夫网，它是用无向图描述的图模型，可刻画联合分布与条件独立关系。还阐述了其条件独立性质，包含成对、局部、全局马尔可夫性，分别说明了它们的定义及相关公式，如成对马尔可夫性的P(Yu,Yv|Yo) = P(Yu|Yo)P(Yv|Yo)等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

参考：http://blog.youkuaiyun.com/pipisorry/article/details/78396503

马尔可夫网
马尔科夫网是使用无向图描述的图模型，是刻画X上联合分布的一种方法，表示一个分解方式,也表示一组条件独立关系。马尔科夫随机场( Markov random field , MRF),也被称为马尔科夫网络( Markov network )或者无向图模型( undirected graphical model )( Kindermann and Snell, 1980 ),包含一组结点,每个结点都对应着一个变量或一组变量。链接是无向的,即不含有箭头。举个例子，今天的天气只由昨天的天气决定，与前天的天气関係ないです。

与贝叶斯网一样，马尔可夫网可以视为定义了一系列由图结构确定的独立性假设。

条件独立性质

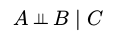
在这里插入图片描述
定义无向图中的3个子集，A,B,C。A和B间的路径均经过集合C,使得A和B被阻隔，A与B相互独立，条件独立性质成立。
条件独立性包含三种：成对、局部、全局马尔可夫性。

成对马尔可夫性
设u和v是无向图G中任意两个没有边连接的节点，节点u和v分别对应随机变量Yu和Yv。其他所有节点为O，对应的随机变量是Yo。成对马尔可夫性是指给定随机变量组Yo的条件下随机变量Yu和Yv是条件独立的，即

P(Yu,Yv|Yo) = P(Yu|Yo)P(Yv|Yo)
成对马尔可夫性（最大团的由来）：
设v∈V是无向图G中任意一个节点，W是与v有边连接的所有节点，O是v、W以外的其他所有节点。v表示随机变量是Yv，W表示的随机变量组是YW，O表示的随机变量组是Yo。局部马尔可夫性是指在给定随机变量组YW的条件下随机变量Yv与随机变量组Yo是独立的，即

P(Yu,Yv|Yw) = P(Yv|Yw)P(Yo|Yw)

在 P(Yo|YW)> 0时，等价地， P(Yv|Yw)= P(Yv|Yw, Yo)
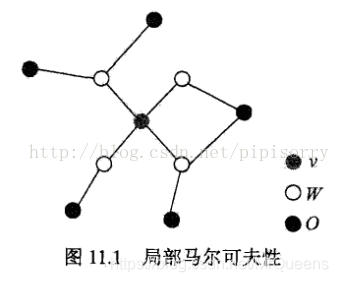
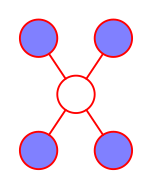
在这里插入图片描述
马尔科夫毯：对于一个无向图,结点 x i 的马尔科夫毯由相邻结点的集合组成。它的性质为:以图中所有剩余变量为条件, x i 的条件概率分布只依赖于马尔科夫毯中的变量。即结点只条件依赖于相邻结点,而条件独立于任何其他的结点。

全局马尔可夫性:
设节点集合A，B是在无向图G中被节点集合C分开的任意节点集合，如下图所示：
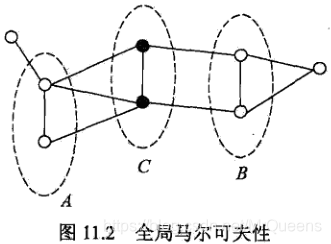
在这里插入图片描述
节点集合A，B和C所对应的随机变量组分别是YA，YB，YC。全局马尔可夫性是指给定随机变量组YC条件下随机变量组YA和YB是条件独立的，即 P(YA,YB| YC) = P(YA|YC)P(YB|YC)