另一个树的子树

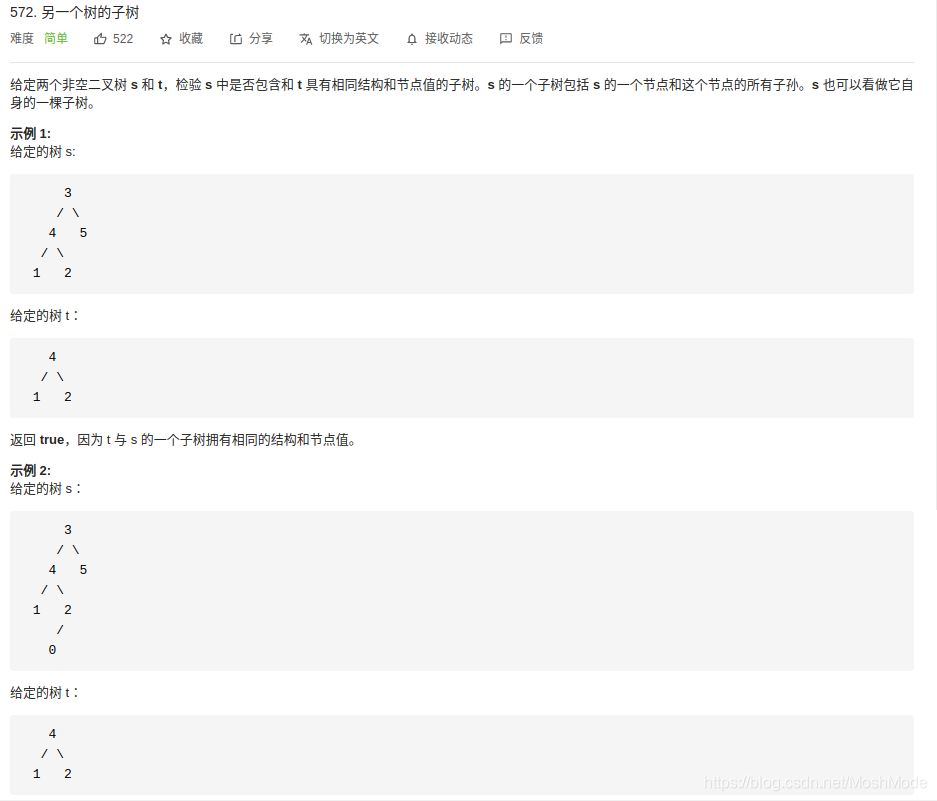
题目

题解

我的题解：深度优先搜索暴力匹配

提供递归辨别是否子树的辨别方法
在要求方法中递归调用

public class DecisionSubtree {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (root == null && subRoot == null) {
            return true;
        }
        if (root == null) {
            return false;
        }

        return decision(root, subRoot) || isSubtree(root.right, subRoot) || isSubtree(root.left, subRoot);
    }

    public boolean decision(TreeNode root, TreeNode subRoot){
        if (root == null && subRoot == null) {
            return true;
        }

        if (root != null && subRoot != null && root.val == subRoot.val) {
            return decision(root.left, subRoot.left) && decision(root.right, subRoot.right);
        }

        return false;
    }
}

官方题解：

KMP：

class Solution {
    List<Integer> sOrder = new ArrayList<Integer>();
    List<Integer> tOrder = new ArrayList<Integer>();
    int maxElement, lNull, rNull;

    public boolean isSubtree(TreeNode s, TreeNode t) {
        maxElement = Integer.MIN_VALUE;
        getMaxElement(s);
        getMaxElement(t);
        lNull = maxElement + 1;
        rNull = maxElement + 2;

        getDfsOrder(s, sOrder);
        getDfsOrder(t, tOrder);

        return kmp();
    }

    public void getMaxElement(TreeNode t) {
        if (t == null) {
            return;
        }
        maxElement = Math.max(maxElement, t.val);
        getMaxElement(t.left);
        getMaxElement(t.right);
    }

    public void getDfsOrder(TreeNode t, List<Integer> tar) {
        if (t == null) {
            return;
        }
        tar.add(t.val);
        if (t.left != null) {
            getDfsOrder(t.left, tar);
        } else {
            tar.add(lNull);
        }
        if (t.right != null) {
            getDfsOrder(t.right, tar);
        } else {
            tar.add(rNull);
        }
    }

    public boolean kmp() {
        int sLen = sOrder.size(), tLen = tOrder.size();
        int[] fail = new int[tOrder.size()];
        Arrays.fill(fail, -1);
        for (int i = 1, j = -1; i < tLen; ++i) {
            while (j != -1 && !(tOrder.get(i).equals(tOrder.get(j + 1)))) {
                j = fail[j];
            }
            if (tOrder.get(i).equals(tOrder.get(j + 1))) {
                ++j;
            }
            fail[i] = j;
        }
        for (int i = 0, j = -1; i < sLen; ++i) {
            while (j != -1 && !(sOrder.get(i).equals(tOrder.get(j + 1)))) {
                j = fail[j];
            }
            if (sOrder.get(i).equals(tOrder.get(j + 1))) {
                ++j;
            }
            if (j == tLen - 1) {
                return true;
            }
        }
        return false;
    }
}

HASH：

class Solution {
    static final int MAX_N = 1005;
    static final int MOD = 1000000007;
    boolean[] vis = new boolean[MAX_N];
    int[] p = new int[MAX_N];
    int tot;
    Map<TreeNode, int[]> hS = new HashMap<TreeNode, int[]>();
    Map<TreeNode, int[]> hT = new HashMap<TreeNode, int[]>();

    public boolean isSubtree(TreeNode s, TreeNode t) {
        getPrime();
        dfs(s, hS);
        dfs(t, hT);

        int tHash = hT.get(t)[0];
        for (Map.Entry<TreeNode, int[]> entry : hS.entrySet()) {
            if (entry.getValue()[0] == tHash) {
                return true;
            }
        }

        return false;
    }

    public void getPrime() {
        vis[0] = vis[1] = true;
        tot = 0;
        for (int i = 2; i < MAX_N; ++i) {
            if (!vis[i]) {
                p[++tot] = i;
            }
            for (int j = 1; j <= tot && i * p[j] < MAX_N; ++j) {
                vis[i * p[j]] = true;
                if (i % p[j] == 0) {
                    break;
                }
            }
        }
    }

    public void dfs(TreeNode o, Map<TreeNode, int[]> h) {
        h.put(o, new int[]{o.val, 1});
        if (o.left == null && o.right == null) {
            return;
        }
        if (o.left != null) {
            dfs(o.left, h);
            int[] val = h.get(o);
            val[1] += h.get(o.left)[1];
            val[0] = (int) ((val[0] + (31L * h.get(o.left)[0] * p[h.get(o.left)[1]]) % MOD) % MOD);
        }
        if (o.right != null) {
            dfs(o.right, h);
            int[] val = h.get(o);
            val[1] += h.get(o.right)[1];
            val[0] = (int) ((val[0] + (179L * h.get(o.right)[0] * p[h.get(o.right)[1]]) % MOD) % MOD);
        }
    }
}