代码如下:
#include <iostream>
using namespace std;
int biSearch(int r[],int N,int x);
int main()
{
int x;
cout << "输入要寻找的数" << endl;
cin>>x;
int r[100];
for(int i=0;i<100;i++)
r[i]=i;
int f;
f=biSearch(r,100,x);
if(f==-1)
cout<<"没有找到"<<endl;
else cout<<"找到了,"<<x<<"在数组下标"<<f<<"位置"<<endl;
return 0;
}
int biSearch(int r[],int N,int x)
{
int start=0,end=N-1,mid;
while(start<=end)
{
mid=start+(end-start)/2;
if(x>r[mid])
{
start=mid+1;
continue;
}
else if(x<r[mid])
{
end=mid-1;
continue;
}
else
return mid;
}
return -1;
}
时间复杂度为O(log N)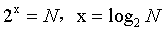




 本文详细解析了二分查找算法的实现,展示了如何在有序数组中查找特定元素,并提供了完整的C++代码示例。通过递归和迭代两种方式,阐述了算法的工作原理,同时分析了其时间复杂度为O(logN),适用于大数据集的高效搜索。
本文详细解析了二分查找算法的实现,展示了如何在有序数组中查找特定元素,并提供了完整的C++代码示例。通过递归和迭代两种方式,阐述了算法的工作原理,同时分析了其时间复杂度为O(logN),适用于大数据集的高效搜索。
















 356
356

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








