八大排序之堆排序

堆排序法（直接选择排序的改进）：将排序码k1,k2,k3,...,kn表示成一棵完全二叉树，然后从第n/2个排序码开妈筛选，使由该结点组成的子二叉树符合堆的定义，然后从第n/2-1个排序码重复刚才操作，直到第一个排序码止，这时候，该二叉树符合堆的定义，初始堆已经建立。

        接着，可以按如下方法进行堆排序：将堆中第一个结点(二叉树根结点)和最后一个结点的数据进行交换(k1与kn)，再将k1--kn-1重新建堆，然后k1和kn-1交换，再将k1--kn-2重新建堆，然后k1和kn-2交换，如此重复下去，每次重新建堆的元素个数不断减1，直到重新建堆的元素个数仅剩一个为止。这时堆排序已经完成，则排序码k1,k2,k3,...kn已排成一个有序序列。

        若排序是从小到大排列，则可以建立大根堆实现堆排序，若排序是从大到小排列，则可以用建立小根堆实现堆排序。

        相关概念：堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足：

    

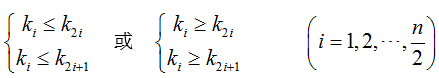
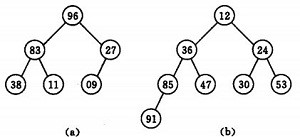
   时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆，或最大项，则对应为大顶堆）。若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。如：

   (a)大顶堆序列：（96, 83,27,38,11,09)

   (b)小顶堆序列：（12，36，24，85，47，30，53，91）

   初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树（一维数组存储二叉树），调整它们的存储序，使之成为一个堆，将堆顶元素输出，得到n个元素中最小(或最大)的元素，这时堆的根节点的数最小（或者最大）。然后对前面(n-1)个元素重新调整使之成为堆，输出堆顶元素，得到n个元素中次小(或次大)的元素。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。称这个过程为堆排序。

因此，实现堆排序需解决两个问题：

1.如何将n个待排序的数建成堆；

2.输出堆顶元素后，怎样调整剩余n-1个元素，使其成为一个新堆。

首先建堆方法：对初始序列建堆的过程，就是一个反复进行筛选的过程。

1）n个结点的完全二叉树，则最后一个结点是第n/2个结点的子树。

2）筛选从第n/2个结点为根的子树开始，该子树成为堆。

3）之后向前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点。

如图建堆初始过程：无序序列：（49，38，65，97，76，13，27，49）

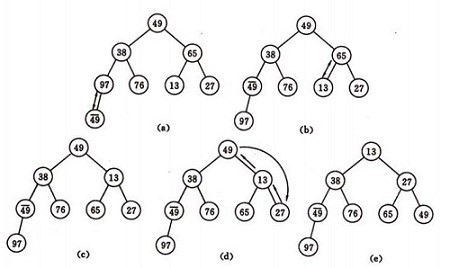
然后讨论第二个问题：输出堆顶元素后，对剩余n-1元素重新建成堆的调整过程。调整小顶堆的方法：

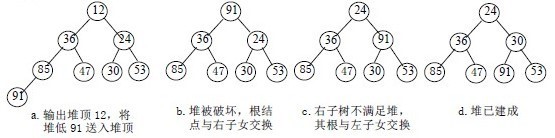
1）设有m个元素的堆，输出堆顶元素后，剩下m-1个元素。将堆底元素送入堆顶（（最后一个元素与堆顶进行交换），堆被破坏，其原因仅是根结点不满足堆的性质。

2）将根结点与左、右子树中较小元素的进行交换。（小顶堆是小元素在上面，所以与较小的元素交换，大顶堆是较大的元素在上面，所以与较大的元素交换）。

3）若与左子树交换，如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复方法（2）.

4）若与右子树交换，如果右子树堆被破坏，即右子树的根结点不满足堆的性质。则重复方法 （2）.

5）继续对不满足堆性质的子树进行上述交换操作，直到叶子结点，堆被建成。

称这个自根结点到叶子结点的调整过程为筛选。如图：

堆排序实现：

package com.eight.paixu;

public class HeapSort {

	public static void main(String[]args) {  
	       int a[] = { 49, 38, 65, 97,76, 13, 27, 49 };  
	        HeapSort obj = new HeapSort();  
	         
	        System.out.print("初始数组： ");  
	       obj.print(a);  
	   
	       for (int i = 0;i <a.length;i++) {  
	           //创建堆,创建的是大顶堆。每次循环完，二叉树的根节点都是最大值，所以与此时的未排好部分最后一个值交换位置  
	           obj.createLittleHeap(a,a.length - 1 - i);  
	           //与最后一个值交换位置，最大值找到了位置  
	           obj.swap(a, 0, a.length - 1 - i);  
	            System.out.printf("第%d躺排序：",i);  
	           obj.print(a);  
	        }  
	   
	        System.out.print("最终结果：");  
	       obj.print(a);  
	    }  
	   
	   //创建大顶堆（升序排序）：双亲节点大于子节点的值。从叶子节点开始，直到根节点。这样建立的堆定位最大值  
	   private void createLittleHeap(int[]data,int last) {  
	       //找到最后一个叶子节点的双亲节点  
	       for (int i =last / 2;i >= 0;i--) {  
	           //保存当前正在判断的节点  
	           int parent =i;  
	           //若当前节点的左子节点存在，即子节点存在  
	           while (2 *parent + 1 <=last) {  
	               //由于创建大顶堆，所以大的元素要换上来，biggerIndex总是记录较大节点的值，先赋值为当前判断节点的左子节点  
	               int bigger = 2 *parent + 1;  
	                 
	               //说明存在右子节点  
	               if (bigger <last) {  
	                   //左子节点  <右子节点时  
	                   if (data[bigger] < data[bigger + 1]) {  
	                       bigger =bigger + 1;  
	                    }  
	                }  
	                 
	               //若双亲节点值小于于子节点中较大的，则交换2者得值（创建大顶堆，大的元素要上来）  
	               if (data[parent] < data[bigger]) {  
	                    swap(data,parent,bigger);  
	                   parent =bigger;  
	                }else{  
	                   break;  
	                }  
	            }  
	        }  
	    }  
	   
	   public void print(int a[]) {  
	       for (int i = 0;i <a.length;i++) {  
	            System.out.print(a[i]+"\t" );  
	        }  
	        System.out.println();  
	    }  
	   
	   public void swap(int[]data,int i,int j) {  
	       if (i ==j) {  
	           return;  
	        }  
	       data[i] = data[i] + data[j];  
	       data[j] = data[i] - data[j];  
	       data[i] = data[i] - data[j];  
	    }  
}