重建二叉树

    二叉树是我们学习数据结构阶段一个重要的知识点，二叉树又被分为满二叉树，完全二叉树和其它三种来学习，所谓的满二叉树是指我们的二叉树的每一个非叶子节点一定含有左孩子和右孩子，而完全二叉树则是指我们的树的叶子节点必须连续的分布在树的左边。

    今天，我们来探索一下如何在知道二叉树前序遍历顺序及中序遍历顺序来重建二叉树

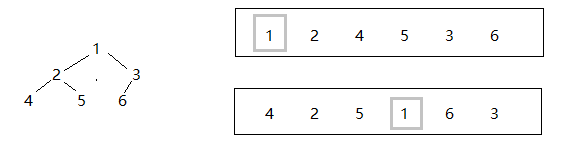
    首先，重建我们的二叉树，必须要找到根节点，那么根节点应该如何找到呢。如下图所示，根结点必定是我们前序遍历数组的首元素。在知道了根节点的情况下，我们就可以在我们的中序遍历序列里找到我们需要的根节点所在。只要有了根节点的位置，我们很容易就可以确定左树节点个数，以及右树的节点个数。而我们很清楚，在二叉树这里我们大多采用递归来解决子问题，所以显而易见的，我们将根节点的左子树和右子树转换成为子问题来解决更加容易理解。

    下面我给出了本题的详细代码以及注释

struct BinaryTreeNode
{
	int _value;
	BinaryTreeNode *_left;
	BinaryTreeNode *_right;
	BinaryTreeNode(const int& x = 0) :_value(x), _left(NULL), _right(NULL)
	{}
};
class BinaryTree
{
private:
	BinaryTreeNode *_root;
public:
	BinaryTree()
	{}
	BinaryTree(int *PreOrder, int *InOrder,int size)
	{
		if (!PreOrder || !InOrder || size <= 0)
			return;
		_root = _CreateTree(PreOrder, PreOrder + size - 1, InOrder, InOrder + size - 1);
	}
private:
	BinaryTreeNode* _CreateTree(int *Pre,int *endPre,int *In,int *endIn)
	{
		//构造当前根节点root 
		int RootValue = Pre[0];
		BinaryTreeNode *root = new BinaryTreeNode(RootValue);
		
		//当走到最后一个元素
		if (Pre == endPre)
		{
			//如果中序也走到了最后一个节点
			//最后一个节点相等说明最后一个节点是一个右分支
			if (In == endIn && *Pre == *In)
				return root;
		}

		//在中序遍历中找到根节点
		int *rootIn = In;
		while (rootIn <= endIn && *rootIn != RootValue)
		{
			//当它等于前序首元素时表示为中序的根节点
			++rootIn;
		}
		//找到之后计算出左子树的节点数
		int leftLen = rootIn - In;

		//找出前序里左子树的构造区间
		int *PreLeftEnd = Pre + leftLen;
		if (leftLen > 0)
		{
			//构造左子树
			root->_left = _CreateTree(Pre + 1, PreLeftEnd  , In, rootIn - 1);
		}

		if (leftLen < endPre - Pre)
		{
			//构造右子树
			root->_right = _CreateTree(PreLeftEnd + 1, endPre, rootIn + 1, endIn);
		}
		return root;

	}
};
int main()
{
	int Pre[] = { 1, 2, 4, 5, 3, 6 };
	int In[] = { 4, 2, 5, 1, 6, 3};
	BinaryTree tree(Pre, In, sizeof(Pre) / sizeof(Pre[0]));
	getchar();
	return 0;
}

    如果实在不能理解建议在纸上将整个过程整理一遍，相信这样就会对树的建立以及递归的算法有深刻的理解，显然博主就经常这么做~

本文出自 “Zimomo” 博客，请务必保留此出处http://zimomo.blog.51cto.com/10799874/1770149