数据结构之二叉树：二叉查找树的先序、中序、后序、层序遍历，Python代码实现——10(续)

数据结构之二叉查找树的代码实现

本节继续对上一节BST的功能实现
在实现之前，先对要实现的功能进行一下简单的介绍

BST的几种常见遍历方式

以一个简化的树为例，一棵树包含根(父)结点和其左子树及右子树：

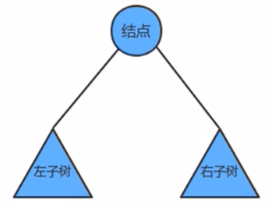
遍历顺序的先后是指根(父)结点被遍历的相对顺序

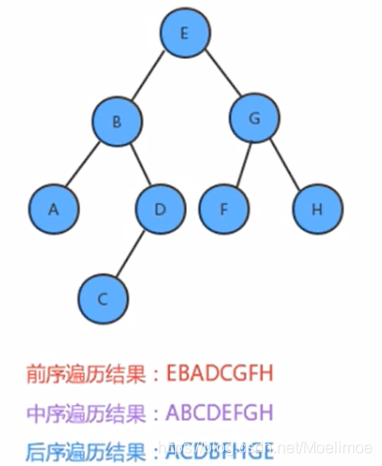
1. 先序遍历：指的是“先根后左再右”
2. 中序遍历：指的是“先左后根再右”
3. 后序遍历：指的是“先左后又再根”

如果子树也存在子树，则也需按此规则进行遍历，一般是递归地进行遍历

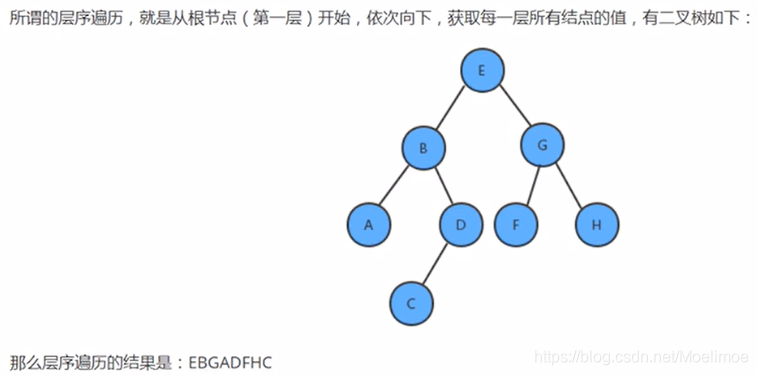
4. 层序遍历：指按树层次顺序，从根结点往下，子结点从左到右地遍历

5. 获取树的最大深度：

• 实现步骤（使用递归）:
  1.如果根结点为空,则最大深度为0 ;
  2.计算左子树的最大深度;
  3.计算右子树的最大深度;
  4.当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1

接下来对BST的这些遍历功能进行实现

实现功能

1. pre_ergodic()实现BST的先序遍历，返回遍历的元素组成的列表
2. mid_ergodic()实现BST的中序遍历，返回遍历的元素组成的列表
3. post_ergodic()实现BST的后序遍历，返回遍历的元素组成的列表
4. layer_ergodic()实现BST的层序遍历，返回遍历的元素组成的列表
5. max_depth()获取树的最大深度

Python代码实现

注：注释的测试代码是前一节的实现，可以忽略

import operator


class Node:
    def __init__(self, key=None, value=None):
        self.key = key
        self.value = value
        self.left = None
        self.right = None


class BinarySearchTree:
    def __init__(self):
        self.root = None
        self.len = 0

    def size(self):
        return self.len

    def put(self, _key, _value):
        """Put an element into this tree and generate a new BST"""
        def put_into(node, _key, _value):
            """Adjust position of new inserted node
            by BST character:left > root > right"""
            if not node:
                self.len += 1
                return Node(_key, _value)
            if operator.lt(_key, node.key):
                node.left = put_into(node.left, _key, _value)
            elif operator.gt(_key, node.key):
                node.right = put_into(node.right, _key, _value)
            elif operator.eq(_key, node.key):
                node.value = _value
            return node
        self.root = put_into(self.root, _key, _value)
        return self.root

    def get(self, _key):
        """Get a value responding to the given _key from this tree"""
        def get_value_by_key(node, _key):
            if not node:
                return
            if operator.lt(_key, node.key):
                return get_value_by_key(node.left, _key)
            elif operator.gt(_key, node.key):
                return get_value_by_key(node.right, _key)
            else:
                return node.value
        return get_value_by_key(self.root, _key)
    #
    # def delete(self, _key):
    #     """Delete a node responding to the giving key(_key)"""
    #     def delete_value_by_key(node, _key):
    #         if not node:
    #             return
    #         if operator.lt(_key, node.key):
    #             node.left = delete_value_by_key(node.left, _key)
    #         elif operator.gt(_key, node.key):
    #             node.right = delete_value_by_key(node.right, _key)
    #         else:
    #             self.len -= 1
    #             to_delete_node = node
    #             if node == self.root:
    #                 self.root = None
    #                 return
    #             # node = None
    #             if not to_delete_node.left:
    #                 return to_delete_node.right
    #             elif not to_delete_node.right:
    #                 return to_delete_node.left
    #             else:
    #                 min_right_tree = to_delete_node.right
    #                 pre = min_right_tree
    #                 while min_right_tree.left:
    #                     pre = min_right_tree
    #                     min_right_tree = min_right_tree.left
    #                 pre.left = None
    #                 min_right_tree.left = to_delete_node.left
    #                 min_right_tree.right = to_delete_node.right
    #                 return min_right_tree
    #     return delete_value_by_key(self.root, _key)
    #
    # def min_key(self):
    #     """Find the minimum key"""
    #     def min_node(node):
    #         while node.left:
    #             node = node.left
    #         return node
    #     return min_node(self.root).key
    #
    # def max_key(self):
    #     """Find the maximum key"""
    #     def max_node(node):
    #         while node.right:
    #             node = node.right
    #         return node
    #     return max_node(self.root).key

    def pre_ergodic(self):
        """Get every key of this tree, pre_ergodic; Return a list of its keys"""
        def pre_ergodic(node, keys_list):
            """Root --> Left --> Right"""
            if not node:
                return
            keys_list.append(node.key)
            if node.left:
                pre_ergodic(node.left, keys_list)
            if node.right:
                pre_ergodic(node.right, keys_list)
        keys_list = []
        pre_ergodic(self.root, keys_list)
        return keys_list

    def mid_ergodic(self):
        def mid_ergodic(node, keys_list):
            """Left --> Root --> Right"""
            if not node:
                return
            if node.left:
                mid_ergodic(node.left, keys_list)
            keys_list.append(node.key)
            if node.right:
                mid_ergodic(node.right, keys_list)

        keys_list = []
        mid_ergodic(self.root, keys_list)
        return keys_list

    def post_ergodic(self):
        def post_ergodic(node, keys_list):
            """Left --> Right --> Root"""
            if not node:
                return
            if node.left:
                post_ergodic(node.left, keys_list)
            if node.right:
                post_ergodic(node.right, keys_list)
            keys_list.append(node.key)
        keys_list = []
        post_ergodic(self.root, keys_list)
        return keys_list

    def layer_ergodic(self):
        """Root-->Left --> Right"""
        queue = [self.root]
        keys = []
        while queue:
            node = queue.pop(0)
            keys.append(node.key)
            if node.left:
                queue.append(node.left)
            if node.right: 
                queue.append(node.right)
        return keys

    def max_depth(self):
        """Get the max depth of this tree"""
        def max_depth(node):
            max_left, max_right = 0, 0
            if not node:
                return 0
            if node.left:
                max_left = max_depth(node.left)
            if node.right:
                max_right = max_depth(node.right)
            return max(max_left, max_right) + 1
        return max_depth(self.root)

代码测试

if __name__ == '__main__':
    BST = BinarySearchTree()

    BST.put('e', '5')
    BST.put('b', '2')
    BST.put('g', '7')
    BST.put('a', '1')
    BST.put('d', '4')
    BST.put('f', '6')
    BST.put('h', '8')
    BST.put('c', '3')
    print(f"The size of this binary tree now is {BST.size()}\n")

    print("pre_order:\n", [(key, BST.get(key)) for key in BST.pre_ergodic()])
    print("mid_order:\n", [(key, BST.get(key)) for key in BST.mid_ergodic()])
    print("post_order:\n", [(key, BST.get(key)) for key in BST.post_ergodic()])
    print("layer_order:\n", [(key, BST.get(key)) for key in BST.layer_ergodic()])
    print(f"Get the maximum depth of this tree: {BST.max_depth()}")

测试结果

The size of this binary tree now is 8

pre_order:
 [('e', '5'), ('b', '2'), ('a', '1'), ('d', '4'), ('c', '3'), ('g', '7'), ('f', '6'), ('h', '8')]
mid_order:
 [('a', '1'), ('b', '2'), ('c', '3'), ('d', '4'), ('e', '5'), ('f', '6'), ('g', '7'), ('h', '8')]
post_order:
 [('a', '1'), ('c', '3'), ('d', '4'), ('b', '2'), ('f', '6'), ('h', '8'), ('g', '7'), ('e', '5')]
layer_order:
 [('e', '5'), ('b', '2'), ('g', '7'), ('a', '1'), ('d', '4'), ('f', '6'), ('h', '8'), ('c', '3')]
Get the maximum depth of this tree: 4

Process finished with exit code 0

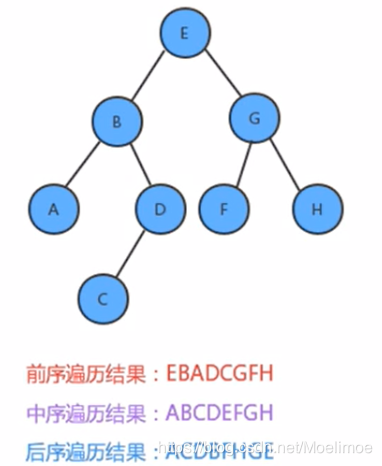
根据前/后序+中序确定这颗二叉查找树：

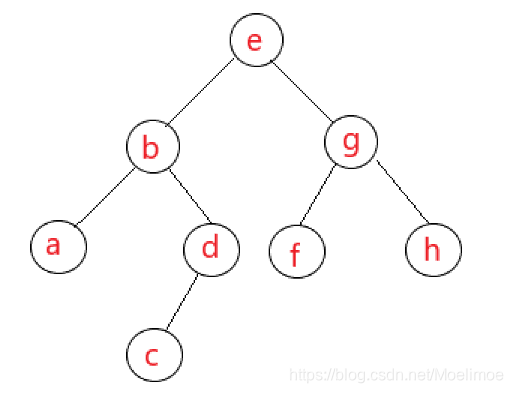
最大深度显然是4