%load_ext autoreload
%autoreload2
import sys
sys.path.append("..")
# import the modules and functions
import torch
from pann_net import PANN, EulerCell_boost
from pann_utils import evaluate
# define circuit parameters and network variables
L, Co, Ro, RC, RL, Rdson, Vf = 250e-6, 25e-4, 20, 0.24, 0.12, 0.207, 20
Ts = 1/20e3
Tslen = 100
dt = Ts/Tslen
class MyEulerCell(EulerCell_boost):
def __init__(self, *args, **kwargs):
super(MyEulerCell, self).__init__()
# 添加自定义初始化逻辑
boost_Euler_cell = torch.jit.script(EulerCell_boost(dt, L, Co, Ro, RC, RL, Rdson, Vf)) # define the Euler cell for DAB
pann_boost = torch.jit.script(PANN(boost_Euler_cell)) # define the PANN for DAB
print(pann_boost)
import numpy as np
from pann_utils import duty_cycle_mod, get_inputs
Vin, Vref = 12, 23
D0 = Vref/Vin
Tsim = 200*Ts # simulation time, considering 10 times of switching periods
# generate terminal voltage waveform vp given one set of modulation parameters
vp = duty_cycle_mod(D0, Vin, dt, Tsim, Ts)
t = np.arange(0, len(vp)*dt, dt)
#################################################################################
# plot the ac voltage waveforms vp
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(style="darkgrid") # Use a dark grid background for contrast
# Create a figure and axis
plt.figure(figsize=(10, 6))
# Plot the waveforms with Seaborn style enhancements
plt.plot(t[-5*Tslen:]*1e6, vp[-5*Tslen:], label='Terminal Voltage (Vp)',
color=sns.color_palette("muted")[0], linestyle='-', linewidth=2)
# Add a title and labels
plt.title('Waveforms of Terminal Voltage', fontsize=18, weight='bold')
plt.xlabel('Time (us)', fontsize=14)
plt.ylabel('Voltage (V)', fontsize=14)
# Add a grid for better readability (already part of Seaborn darkgrid)
plt.grid(True)
# Add a legend to describe the waveforms
plt.legend(loc='upper right', fontsize=12)
# Show the plot
plt.tight_layout() # Adjust layout for better fit
plt.show()
# construct inputs tensor in numpy
inputs = vp[None, :, None]
print(inputs.shape, type(inputs)) # inputs should be of shape (bs x seq_len x inp_dim)
# convert to torch FloatTensor
inputs = torch.FloatTensor(inputs)
print(inputs.shape, type(inputs))
# initialize the state variable
state_dim = 2
state0 = torch.zeros((inputs.shape[0], 1, state_dim))
# use PANN to infer the state variable iL
pann_boost.eval()
with torch.no_grad():
# don't capture the computational graph, as this is not training
states = pann_boost(inputs, state0)
print(states.shape, type(states))
#################################################################################
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
%matplotlib notebook
# if use google colab
# %matplotlib widget
if len(inputs.shape) == 3:
t = t[-2*Tslen:]*1e6
inputs = inputs[0, -2*Tslen:]
states = states[0, -2*Tslen:]
# Example data for vp and vs
# inputs: size (seqlen x inp_dim)
# states: size (seqlen x state_dim)
sns.set(style="darkgrid") # Use a dark grid background for contrast
t, inputs, states = np.array(t), np.array(inputs), np.array(states)
vp, iL, vo = inputs[:, 0], states[:, 0], states[:, 1]
# Create figure and subplots (two subplots: one for vp, one for vs)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 9))
ax22 = ax2.twinx() # Create a second axes that shares the same x-axis
# Set limits for both plots
ax1.set_xlim(t.min(), t.max())
ax1.set_ylim(-2, inputs.max()*1.2)
ax2.set_xlim(t.min(), t.max())
ax2.set_ylim(-0.2, states[:, 0].max()*1.2)
ax22.set_ylim(states[:, 1].min()*0.995, states[:, 1].max()*1.005)
# Labels and titles
ax1.set_title('Waveforms of Terminal Voltage', fontsize=15, weight='bold')
ax2.set_title('Waveforms of Inductor Current and Output Voltage', fontsize=15, weight='bold')
# ax1.set_xlabel('Time (us)', fontsize=14)
ax1.set_ylabel('Terminal Voltage (V)', fontsize=14)
ax2.set_xlabel('Time (us)', fontsize=14)
ax2.set_ylabel('Current (A)', fontsize=14)
ax22.set_ylabel('Output Voltage (A)', fontsize=14)
# Initialize empty lines for both plots
line1_1, = ax1.plot([], [], lw=2, label='Terminal Voltage (va)',
color=sns.color_palette("muted")[0], linestyle='-')
line2_1, = ax2.plot([], [], lw=2.5, label='Inductor Current (iL)',
color=sns.color_palette("muted")[1], linestyle='-')
line2_2, = ax22.plot([], [], lw=2.5, label='Output Voltage (vo)',
color=sns.color_palette("muted")[2], linestyle='-.')
dot1_1 = ax1.scatter([], [], edgecolor=sns.color_palette("muted")[0], alpha=0.5,
s=50, color=sns.color_palette("muted")[0], marker="o")
dot2_1 = ax2.scatter([], [], edgecolor=sns.color_palette("muted")[0], alpha=0.5,
s=50, color=sns.color_palette("muted")[0], marker="o")
dot2_2 = ax22.scatter([], [], edgecolor=sns.color_palette("muted")[0], alpha=0.5,
s=50, color=sns.color_palette("muted")[0], marker="o")
dot2_3 = ax2.scatter([], [], edgecolor=sns.color_palette("muted")[4], alpha=0.8,
s=100, color=sns.color_palette("muted")[4], marker="*")
dot2_4 = ax22.scatter([], [], edgecolor=sns.color_palette("muted")[4], alpha=0.8,
s=100, color=sns.color_palette("muted")[4], marker="*")
# Add grids and legends
ax1.grid(True)
ax2.grid(True)
# ax22.grid(False)
ax1.legend(loc='upper right', fontsize=12)
ax2.legend(loc='upper right', fontsize=12)
ax22.legend(loc='center right', fontsize=12)
# Initialize the animation
def init():
line1_1.set_data([], [])
line2_1.set_data([], [])
line2_2.set_data([], [])
dot1_1.set_offsets(np.empty((0, 2))) # Initialize empty scatter for subplot 1
dot2_1.set_offsets(np.empty((0, 2))) # Initialize empty scatter for subplot 2
dot2_2.set_offsets(np.empty((0, 2))) # Initialize empty scatter for subplot 2
dot2_3.set_offsets(np.empty((0, 2))) # Initialize empty scatter for subplot 2
dot2_4.set_offsets(np.empty((0, 2))) # Initialize empty scatter for subplot 2
return line1_1, line2_1, line2_2, dot1_1, dot2_1, dot2_2, dot2_3, dot2_4
# Update the plots
def update(frame):
line1_1.set_data(t[:frame+1], vp[:frame+1]) # Update vp plot progressively
line2_1.set_data(t[:frame+1], iL[:frame+1]) # Update vs plot progressively
line2_2.set_data(t[:frame+1], vo[:frame+1]) # Update iL plot progressively
dot1_1.set_offsets(np.c_[t[frame+1], vp[frame+1]])
dot2_1.set_offsets(np.c_[t[frame], iL[frame]])
dot2_2.set_offsets(np.c_[t[frame], vo[frame]])
dot2_3.set_offsets(np.c_[t[frame+1], iL[frame+1]])
dot2_4.set_offsets(np.c_[t[frame+1], vo[frame+1]])
return line1_1, line2_1, line2_2, dot1_1, dot2_1, dot2_2, dot2_3, dot2_4
# Create the animation
ani = FuncAnimation(fig, update, frames=inputs.shape[0]-1,
init_func=init, blit=False, interval=5)
# save as GIF file
# ani.save('Buck-inference.gif', writer='pillow')
# Show the plot
plt.tight_layout() # Adjust layout for better fit
# Display the animation in Jupyter
plt.show()
pann_net.py文件为:
class EulerCell_boost(nn.Module):
"""
Define Explicit Euler Recurrent Cell of PANN for boost converter
Modified to match the non-ideal state-space equations.
"""
def __init__(self, dt, L, Co, Ro, RC, RL, Rdson, Vf, Vin, **kwargs):
super(EulerCell_boost, self).__init__(**kwargs)
self.dt = dt
self.L = nn.Parameter(torch.Tensor([L]))
self.Co = nn.Parameter(torch.Tensor([Co]))
self.Ro = nn.Parameter(torch.Tensor([Ro])) # Load resistance
self.RC = nn.Parameter(torch.Tensor([RC])) # Capacitor ESR
self.RL = nn.Parameter(torch.Tensor([RL])) # Inductor ESR
self.Rdson = nn.Parameter(torch.Tensor([Rdson])) # MOSFET on-resistance
self.Vf = nn.Parameter(torch.Tensor([Vf])) # Diode forward voltage drop
self.Vin = nn.Parameter(torch.Tensor([Vin])) # Input voltage source
def forward(self, inputs, states):
iL = states[:, 0]
vc = states[:, 1]
duty = inputs[:, 0]
# ON 阶段物理模型
diL_dt_on = (self.Vin - iL * (self.RL + self.Rdson) - vc) / self.L
dvc_dt_on = - vc / self.Co * (self.RC + self.Ro)
# OFF 阶段物理模型
diL_dt_off = (self.Vin - iL * self.RL - vc - self.Vf) / self.L
dvc_dt_off = (iL * self.RL - vc / ((self.RC + self.RL) * self.Co)
# 使用 duty(占空比D) 对两个阶段的状态导数进行加权平均
diL_dt = duty * diL_dt_on + (1 - duty) * diL_dt_off
dvc_dt = duty * dvc_dt_on + (1 - duty) * dvc_dt_off
# 显式欧拉法更新状态
iL_next = iL + self.dt * diL_dt
iL_next = torch.relu(iL_next)
vc_next = vc + self.dt * dvc_dt
return torch.stack((iL_next, vc_next), dim=1)
运行

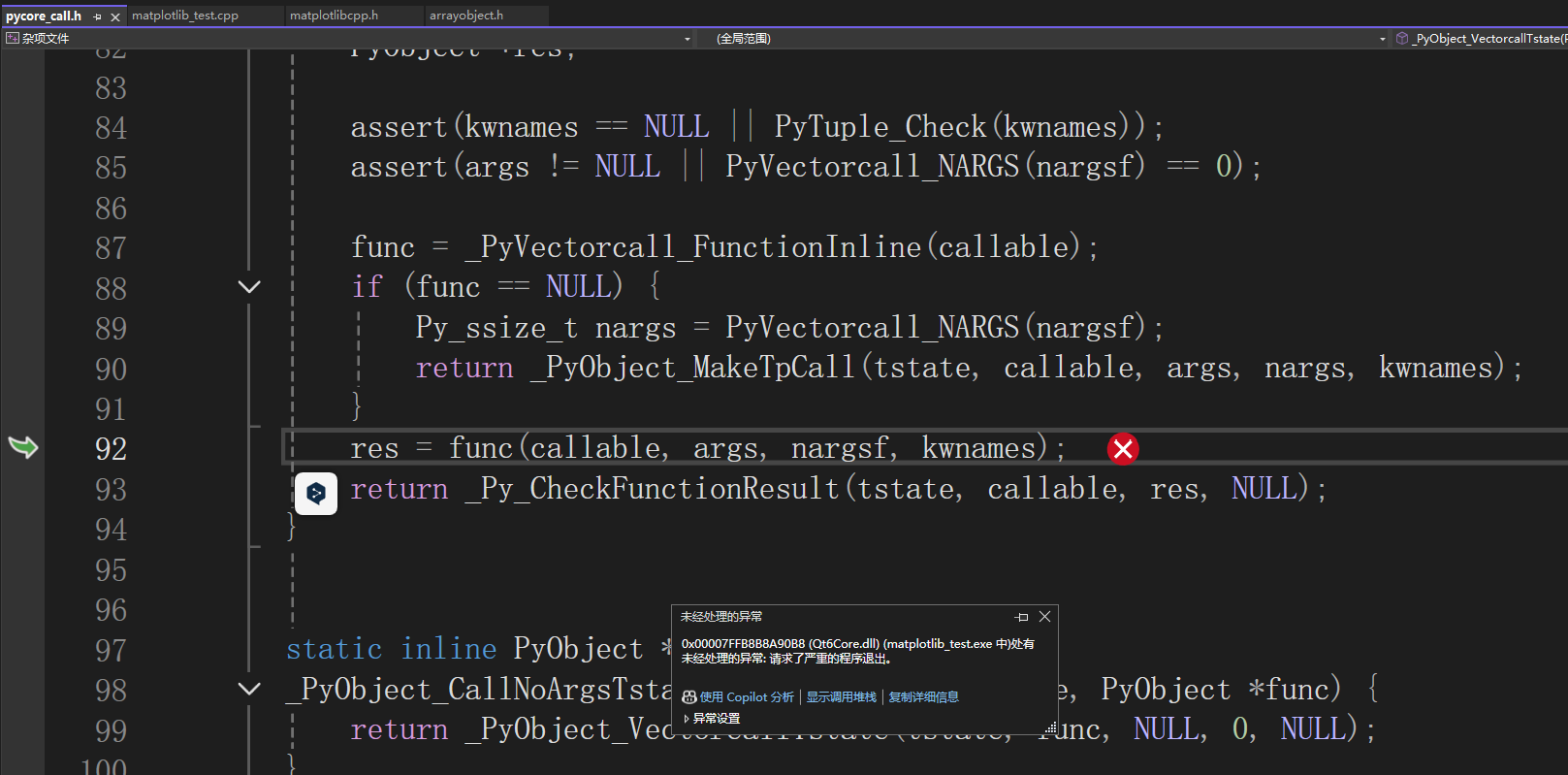
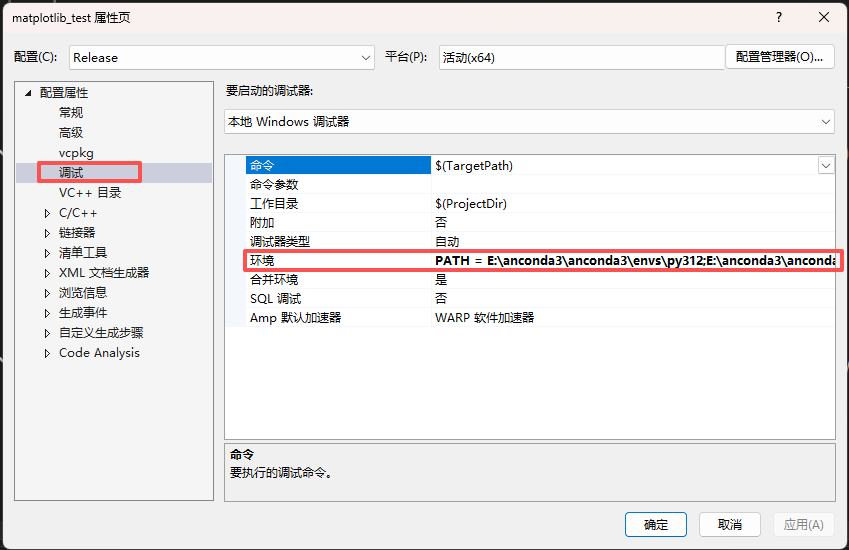
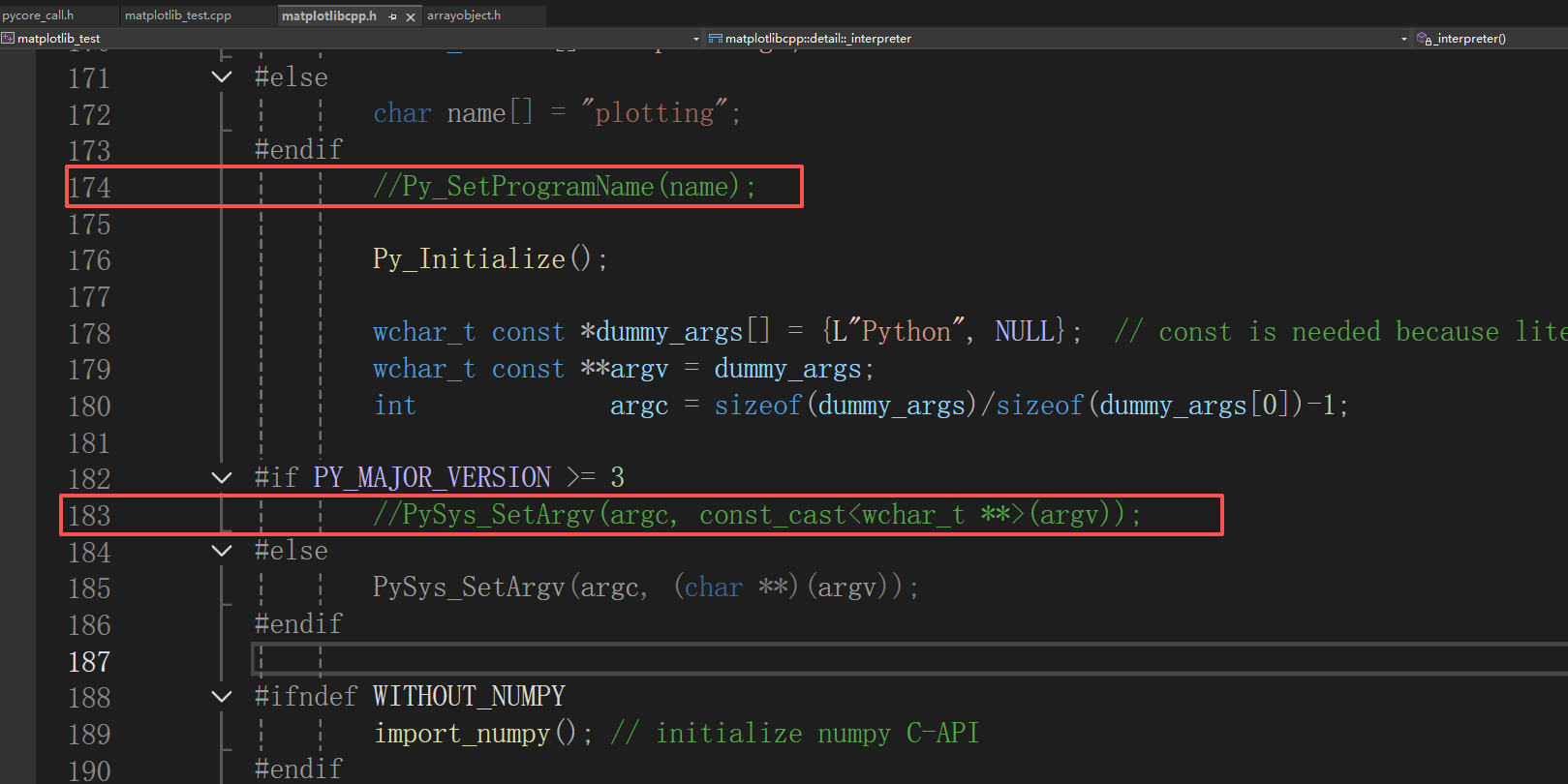





















 799
799

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










