MAC M1大数据0-1成神篇-16 hadoop(hdfs算法篇)_hadoop hdfs g1算法-优快云博客

本文详细介绍了算法复杂度的概念，包括时间复杂度和空间复杂度，强调了它们在评估算法效率时的重要性。通过实例分析了不同排序算法如冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序等的时间复杂度，并讨论了在实际应用中如何在时间与空间之间做出取舍。此外，还提到了特殊算法如计数排序、桶排序和基数排序的特点和适用场景。

写在前面：

因为hadoop和mr涉及到了一些算法，那么我们先讲一些算法吧

进入主题：

1.算法复杂度

算法复杂度分为时间复杂度和空间复杂度。其作用：
- 时间复杂度是指执行这个算法所需要的计算工作量；
- 而空间复杂度是指执行这个算法所需要的内存空间；
时间和空间都是计算机资源的重要体现，而算法的复杂性就是体现在运行该算法时的计算机所需的资源

1.1 空间复杂度

一个程序的空间复杂度是指运行完一个程序所需内存的大小。
利用程序的空间复杂度，可以对程序的运行所需要的内存多少有个预先估计。
程序执行时所需存储空间包括以下两部分
- 固定部分:主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间。
- 可变空间:这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等。
如果判断一个年份是平年还是闰年？
- 方法1：使用年份计算公式进行计算
- 方法2：创建一个长度为4000的数组，以年份为下标，直接取值即可
  - 如果计算的年份超过1万年？

1.2.时间复杂度

一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。

一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)

T(n)=n^2+3n+4
T(n)=4n^2+2n+1
他们执行的频度是不同的，
但是时间复杂度？

为了描述时间频度变化引起的变化规律，引入时间复杂度概念。记为O(…)
时间复杂度计算规则只需要遵循如下守则：
- 用常数1来取代运行时间中所有加法常数；
- 只要高阶项，不要低阶项；
- 不要高阶项系数；
时间频度不同，但时间复杂度可能相同。
- T(n)=n^2+3n+4-->n^2+3n-->n^2
- T(n)=4n^2+2n+1-->4n^2+2n-->4n^2-->n^2
- 它们的频度不同但时间复杂度相同，都为O(n^2)
- T(n)=log2nn+2n+10-->log2nn+2n-->log2n*n-->logN * n
常见的时间复杂度场景(效率对比图)
- O(1)—常数阶
- O(N)—线性阶
- O(logN)—对数阶
- O(n^2)—平方阶
- O(nlogn)—线性对数阶
- O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2^n)<O(n!)<O(n^n)
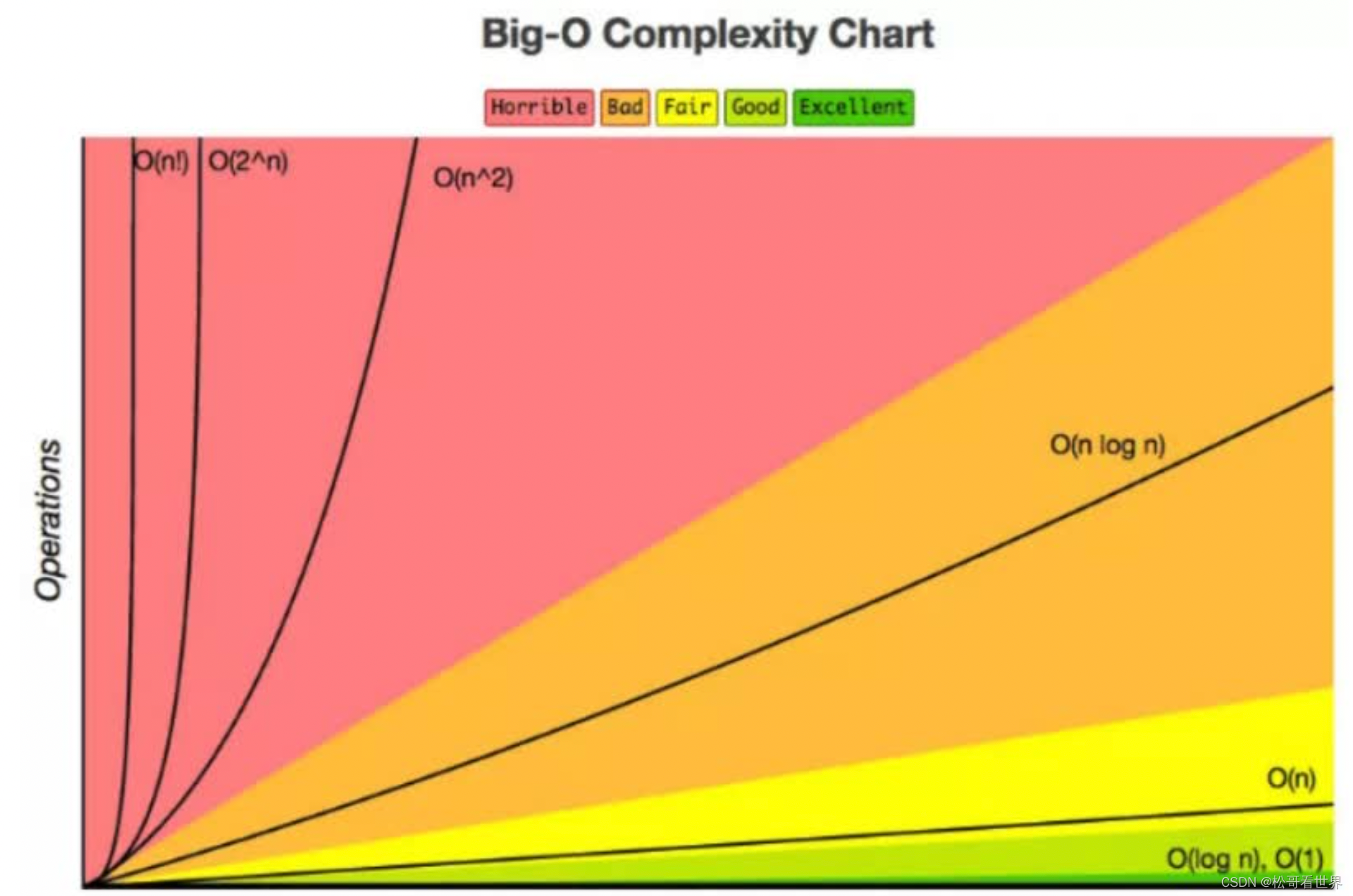
时间复杂度去估算算法优劣的时候注重的是算法的潜力
- 有100条数据的时候算法a比算法b快
- 有10000条数据的时候算法b比算法a快
- 算法b的时间复杂对更优，我们认为谁能处理更多数据，并且速度快，那么就认为哪个更优。

1.3时间与空间的取舍

日常操作中：我们都是更加注重时间复杂度，有些特殊情况下，空间复杂度可能会更加重要
- 因为很多时候空间复杂度可以花钱解决
编程的精髓和美，并不在于一方的退让和妥协。而是在于如何在二者之间取一个平衡点，完成华丽变身
- 但是将来工作中一切以时间复杂度为标准

1.4.十大排序算法

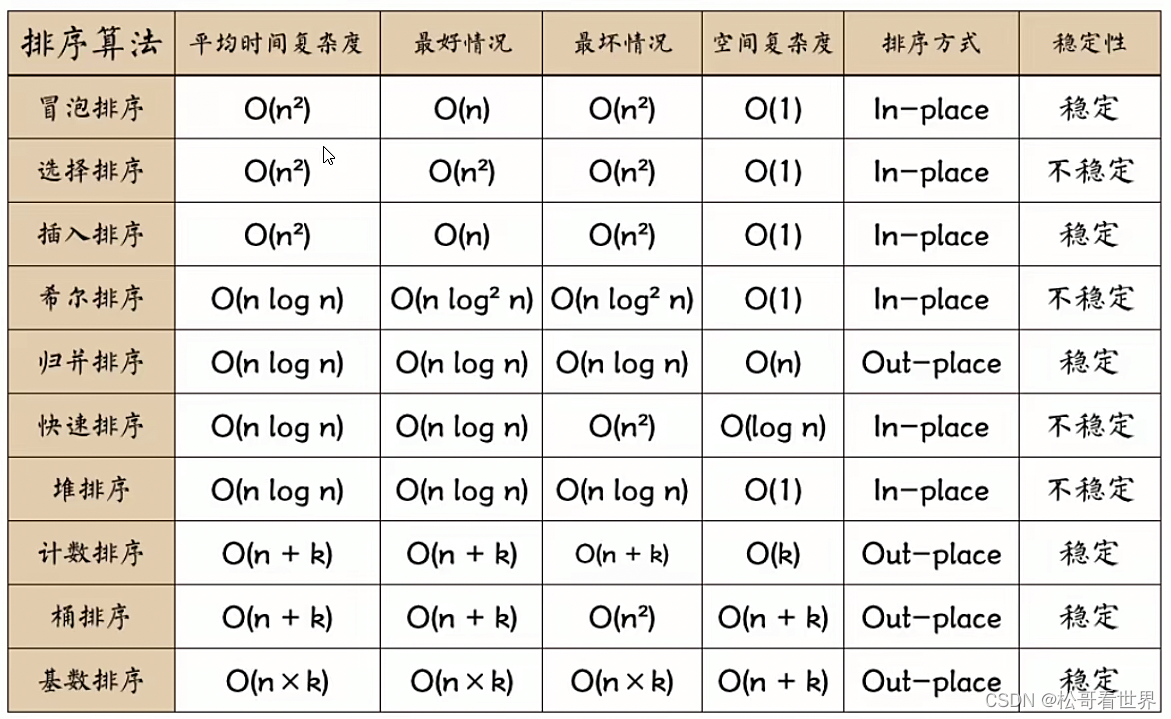
冒泡排序：
- - 从位置0开始，当前位置数字和后面位置的数字进行比较
  - 如果前面的大于后面，数据交换
  - 将位置向后移动一位，重复第一个过程，直到最后一个
  - 重复刚才的过程
  - 时间复杂度O=n^2
选择排序：（最简单，也是最没用的，没用是因为选择排序的时间复杂度高并且还是不稳定的排序方法，项目中很少会用到）
- - 在一个长度为 N 的无序数组中，第一次遍历 n-1 个数找到最小的和第一个数交换。
  - 第二次从下一个数开始遍历 n-2个数，找到最小的数和第二个数交换。
  - 重复以上操作直到第 n-1 次遍历最小的数和第 n-1 个数交换，排序完成。
  - 时间复杂度O=n^2
插入排序：
- - 从第一个元素开始，该元素可以认为已经被排序；
  - 取出下一个元素，在已经排序的元素序列中从后向前扫描；
  - 如果该元素（已排序）大于新元素，将该元素移到下一位置；
  - 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
  - 将新元素插入到该位置后；
  - 重复步骤2~5。
  - 时间复杂度O=n^2
希尔排序：
- - 将数据递归分组，首先分为长度/2组
  - 然后将第一个数字与1+zu进行插入排序，经过第一次在整体排序后，小的数字很快会被移动到前面
  - 重新将数据分组，原来组/2
  - 小的数字很快就会被移动到前面
  - 时间复杂度O=n^1.3
快速排序：
- - 三种（挖坑法左右法前后法）
  - 操作：选择一个数字作为参照物（基准数字）5
  - 思想：然后和另一个的进行比较，如果是右边的小于5就交换，5左面的大于5就交换
  - 整体排序之后，5的位置是正确的，左右两个是无序
  - 将左右两个都当做一个新序列进行排序基准数
  - 时间复杂度O=n*log2n
  - 快速排序怎么快了呢？
    - 比如我们一共8个数进行排序。
    - 用冒泡排序的话就是 8的平方，64次。
    - 那么快速排序会将最后一个或者第一个做完中间值，进行7次比较。情况好的情况下，拆分成了两份就是，3，4。那么就是 7+3的平方+4的平方，7+9+16=32次。
    - 能节约一半时间。
归并排序：
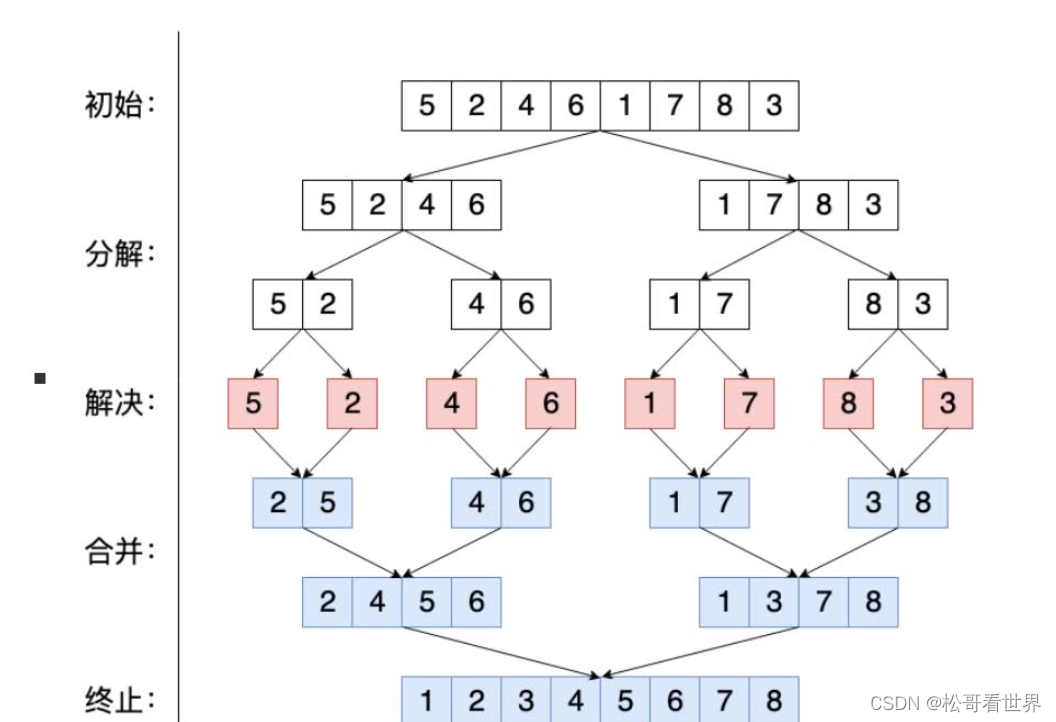
- 让两个有序队列进行比较，然后每个队列依次取出1个数字比较，然后小的数字被去除
- 分割
  - 依次将数列二等分，二等分之后的子序列继续二等分
  - 直到每个子序列只有一个数字，停止分割
- 合并
  - 按照分割的顺序进行合并
快速排序是从中间切开，归并排序这个直接拆，拆到最后一个数。有个缺点，拆了那么多所以就是占内存空间
快速排序和归并排序哪个快？
- 在数组长度小于一千万的时候，快速排序的速度要略微快于归并排序，可能是因为归并需要额外的数组开销（比如声明临时local数组用来储存排序结果），这些操作让归并算法在小规模数据的并不占优势。
- 当数据量达到亿级时，归并的速度开始超过快速排序了，因为归并排序比快排要稳定，所以在数据量大的时候，快排容易达到O(n^2)的时间复杂度，当然这里是指未改进的快排算法。
计数排序：
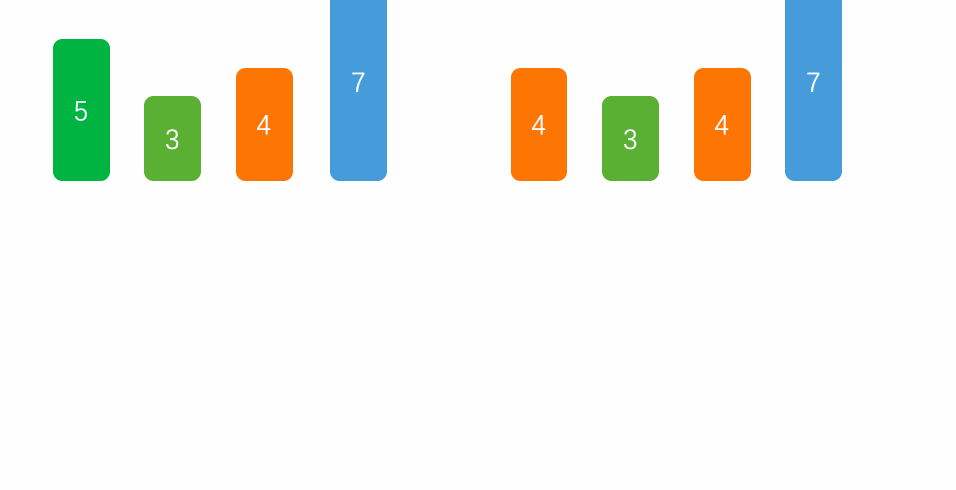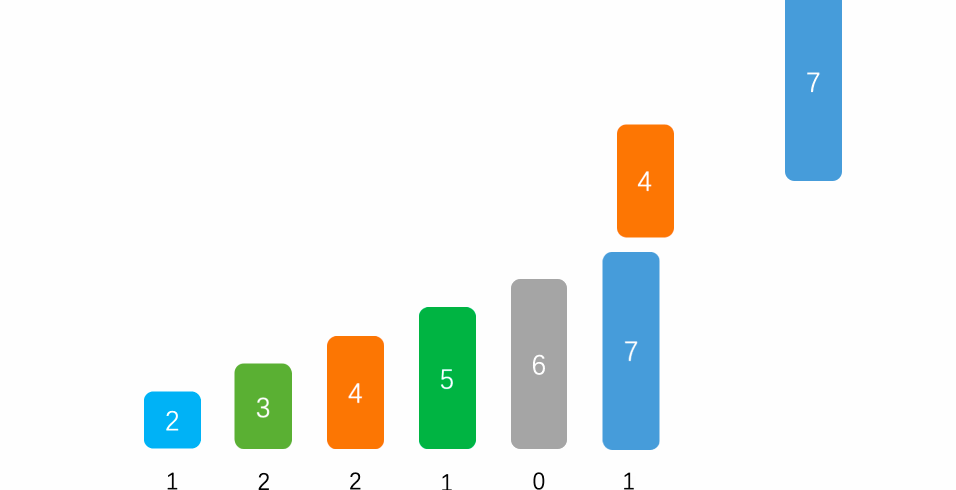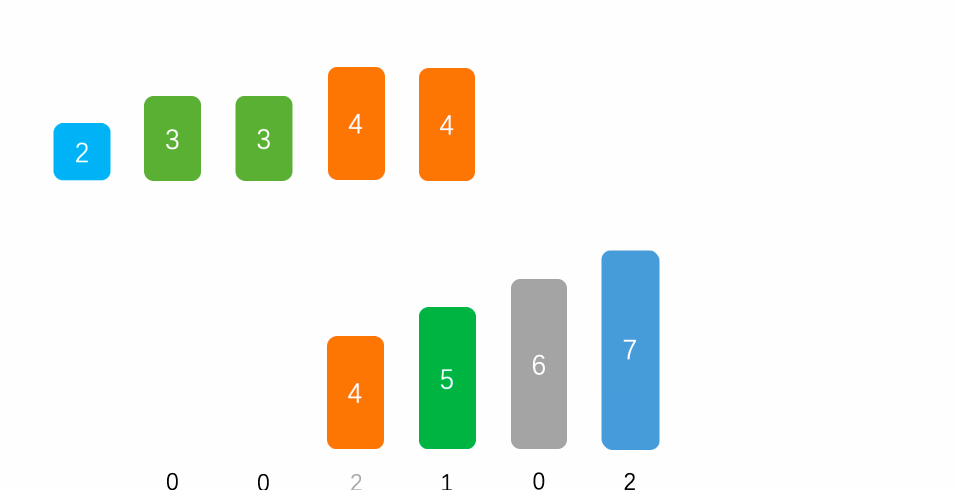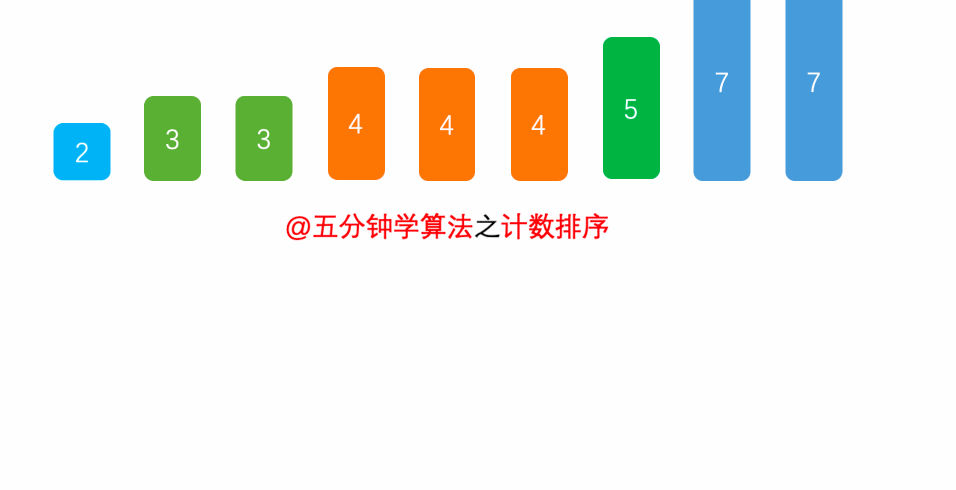
- - 一种很巧妙的排序算法
  - 比较特殊的排序算法，只针对特殊数据的排序
  - 将对应的数据让数组的索引对应值+1
  - 最后遍历数组，索引对应的值是几就打印几
桶排序：
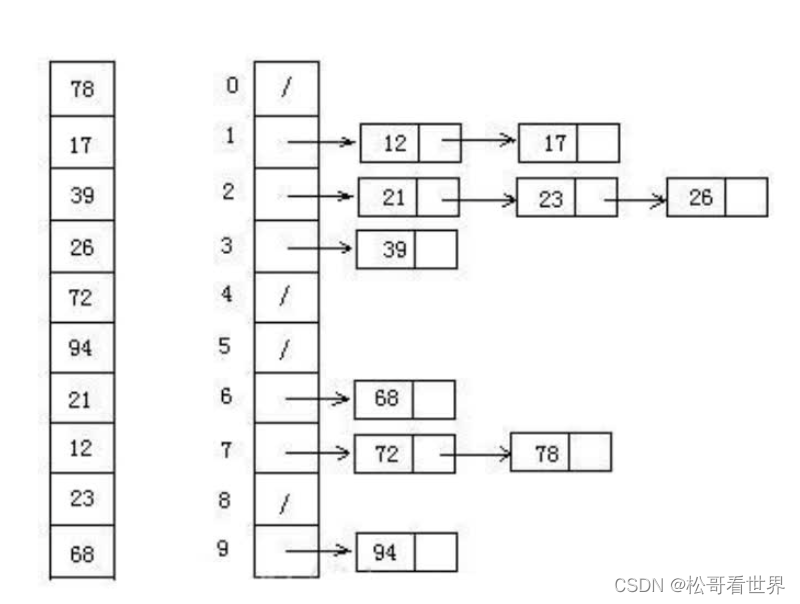
- - 将数字按照范围进行分割
  - 然后对分割后的数据进行排序（继续分割）
  - 将来数据分桶要特别注意数据倾斜的问题