金融市场的 Random Walk Model 以及 stylized facts. 阅读 Trades, Quotes and Prices 的第二章。
数学,统计学,机器学习,人们总是用各种各样的办法研究金融市场。
Originally Posted at: https://clouder0.com/zh-cn/posts/price-change-statistics/
The Random Walk Model
一个相当流行的模型,是将价格变动看作是 Gaussian random walks,即 d p ∼ Gaussian \mathrm{d} p \sim \text{Gaussian} dp∼Gaussian,价格变动服从 i.i.d. 独立同分布的高斯随机变量。价格是 martingales,对明天价格最好的预测就是今天的价格,价格变动是 mean 为 0 的 Gaussian Random Variable.
Bachelier's First Law:price variogram 关于时间 τ \tau τ 线性增长。
$$\mathcal{V}(\tau) := \mathbb{E}[(p_{t+\tau} - p_t)^2] = D\tau$$后续的很多 empirical studies 认为,价格变动应当是一个相乘的关系,或者说关于比例线性。这意味着使用 geometric Brownnian motion 来代替 Brownian motion. 实际上,从 1960 年代开始,这已经成为了金融数学领域的标准模型。
但是在较短的时间尺度上,也有 empirical evidence 认为价格变动更接近于 additive 而非 multiplicative. 一个重要的原因是,市场常常规定了最小价格变动的 ticksize.
在这本书中,因为主要考察短时间,还是会使用 additive model.
但是还是介绍一下另一种:定义 volatility σ r \sigma_r σr:
$$D := \sigma_r^2 \overline{p}^2$$其中 p ‾ \overline{p} p 为当前价格或者某段时间的平均价格。
现在,如果价格变动并不是独立的呢?比如我们知道,一段时间内总是可能出现单边趋势或者反弹。
考虑价格序列:
$$p_t = p_0 + \overline{p}\sum \limits _{t'=0}^{t-1}r_{t'}$$其中 return 序列 r t r_t rt 是 time-stationary 的,且 mean 为 0:
$$\mathbb{E}[r_t]=0$$variance:
$$\mathbb{E}[r_t^2] - \mathbb{E}[r_t]^2 = \sigma_r^2$$可以用 covariance 来表达 dependence:
$$\operatorname{Cov}(r_{t'}, r_{t''}) := \mathbb{E}[r_{t'}r_{t''}] - \mathbb{E}[r_{t'}] - \mathbb{E}[r_{t''}] = \mathbb{E}[r_{t'}r_{t''}]$$考虑到 return series 是 time-stationary 的,这个 covariance 只与 time lag ∣ t ′ − t ′ ′ ∣ |t'-t''| ∣t′−t′′∣ 有关。一个常见的考察是 autocorrelation function(ACF):
$$C_r(\tau) := \dfrac{\operatorname{Cov}(r_t, r_{t+\tau})}{\sigma_r^2}$$在 random walk 中, C r ( τ ) = δ τ , 0 C_r(\tau) = \delta_{\tau,0} Cr(τ)=δτ,0,其中 δ τ , 0 \delta_{\tau,0} δτ,0 是 Kronecker delta function:
$$\delta_{i,j} = \begin{cases} 1, \text{if }i = j\\ 0, \text{otherwise} \end{cases}$$也就是除了 τ = 0 \tau=0 τ=0 时为 1 1 1,其他时候为 0 0 0.
对于 τ > 0 \tau>0 τ>0,一个单边趋势往往有着 C r ( τ ) > 0 C_r(\tau) >0 Cr(τ)>0,也就是价格上涨。而 mean reverting 则有着 C r ( τ ) < 0 C_r(\tau) < 0 Cr(τ)<0.
volatility 本身也和我们采样的时间有关,如果我们每 τ \tau τ 秒采样一个价格,相应的 volatility 为:
$$\sigma^2(\tau) := \dfrac{\mathcal{V}(\tau)}{\tau \overline{p}^2}$$#TODO# 这个式子不知道是怎么来的。当 τ = 1 \tau=1 τ=1 时,有 σ 2 ( 1 ) = σ r 2 \sigma^2(1) = \sigma^2_r σ2(1)=σr2.
代入可以得到:
$$\sigma^2(\tau) = \sigma^2_r \left[ 1 + 2 \sum \limits _{u=1}^\tau \left(1 - \dfrac{u}{\tau} \right) C_r(u) \right]$$
σ ( τ ) \sigma(\tau) σ(τ) 关于 τ \tau τ 的图像称为 volatility signature plot.
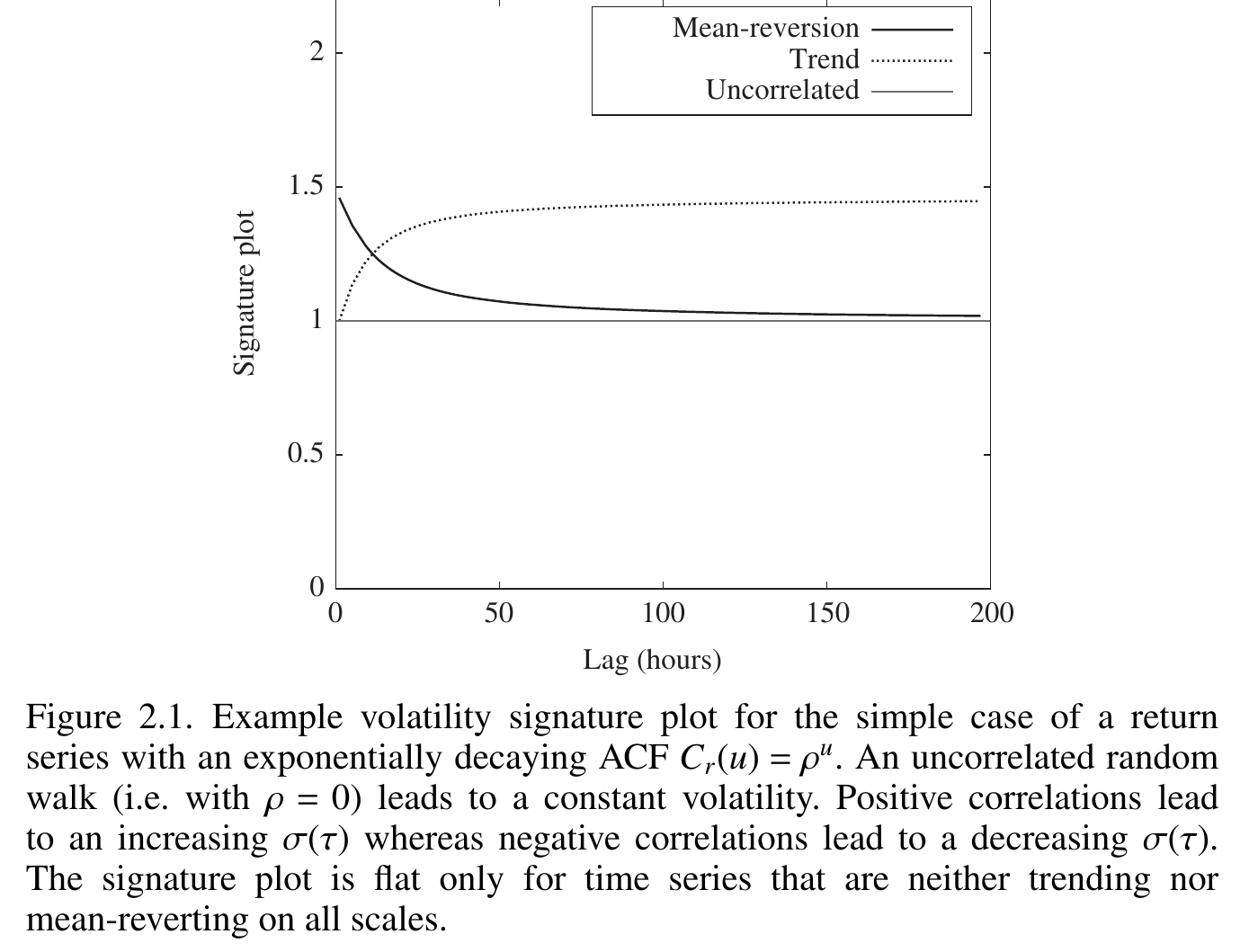
图中的例子是一个指数衰减的 ACF C r ( u ) = ρ u C_r(u) = \rho^u Cr(u)=ρu 画出的。接近直线说明价格的 autocorrelation 不强。
现在假设价格还受到一些 high frequency noise 的影响:
$$p_t = p_0 + \overline{p} \sum \limits _{t'=0}^{t-1}r_{t'} + \eta_t$$其中 noise η t \eta_t ηt 是 mean 为 0、variance 为 σ η 2 \sigma_{\eta}^2 ση2 且与 r t r_t rt 无关的随机变量,但是自相关,并且 ACF 为:
$$C_{\eta}(\tau) := \dfrac{\operatorname{Cov}(\eta_t, \eta_{t+\tau})}{\sigma^2_{\eta}} = e^{-\tau/ \tau_{\eta}}$$其中 τ η \tau_{\eta} τη 是 noise 的自相关时间。
The noise η \eta η is often called an Ornstein–Uhlenbeck process, see, e.g., Gardiner, C. W. (1985). Stochastic methods. Springer, Berlin-Heidelberg.
可以将这个模型解读为:市场价格有时候会偏离真实价格,这个偏离是一个 random error term,在时间尺度 τ η \tau_{\eta} τη 下会 mean-reverts. 另一种解读是,microstructure noise 来自我们对 true price 的估计不准的 error term,也就是我们的 predicted true price 总是和 true price 有一定的偏差,但这个 bias 也会 mean-reverts. 这被称为 bid-ask bounce effect.
加入这项 noise 之后,我们观察到的 square volatility 变成了:
$$\sigma^2(\tau) \to \sigma^2(\tau) + \dfrac{2\sigma^2_{\eta}}{\tau} \left( 1 - e^{-\tau/\tau_{\eta}} \right)$$这个额外的项在 τ = 0 \tau=0 τ=0 时,等于 2 σ η 2 / τ 2\sigma^2_{\eta}/\tau 2ση2/τ,在 τ → ∞ \tau \to \infty τ→∞ 时衰减至 0.这主要会增大短期的 volatility.
Bachelier's first law 假设价格变动之间无关,这对应的是一根直线的 volatility signature plot.
实际上好像大部分时候确实接近一根直线。
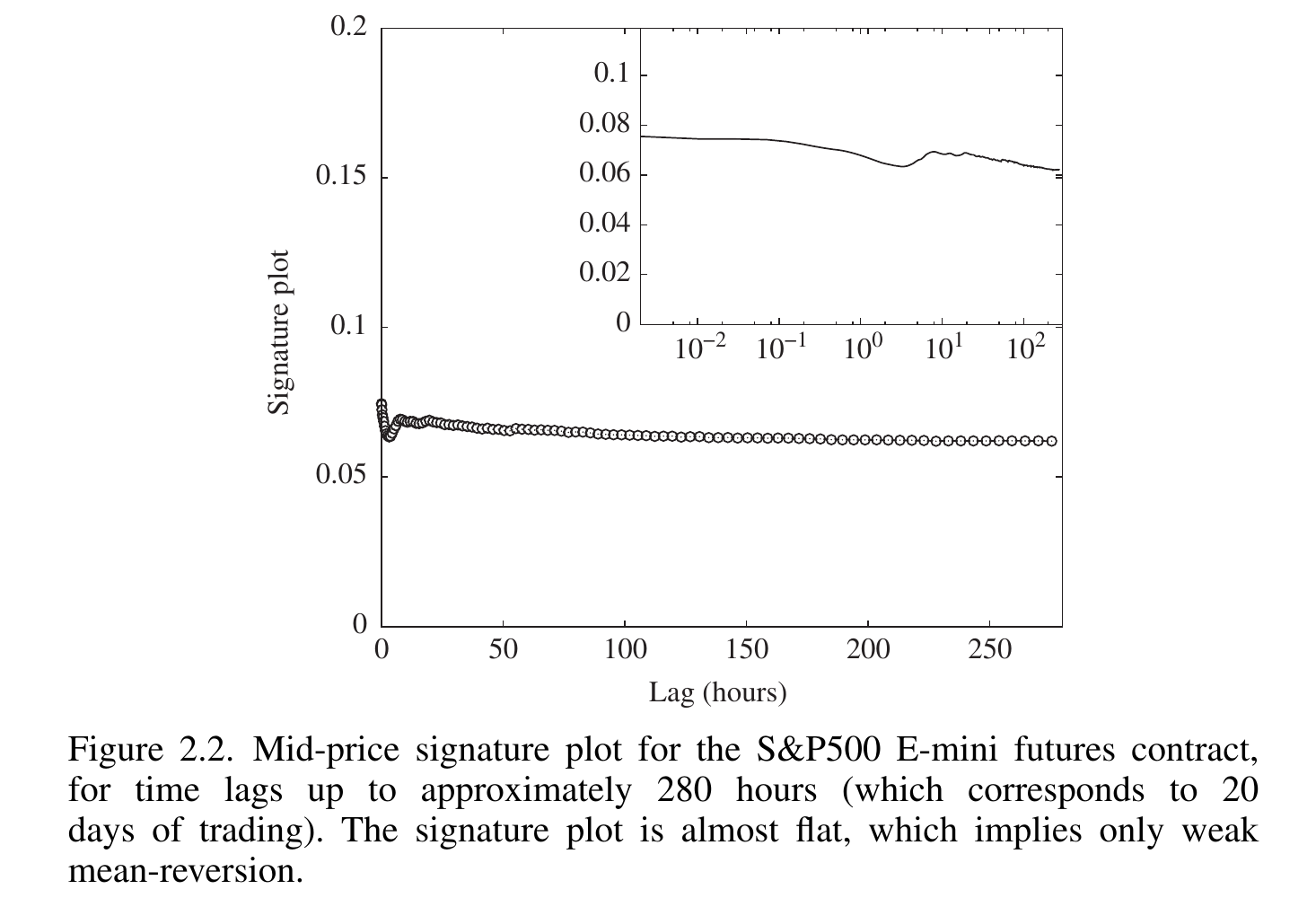
Jumps and Intermittency in Financial Markets
Heavy Tails
很多模型假设 return 服从 Guassian Distribution,但大量研究表明,Gaussian 不是一个好的 model. 实际上的 return 具有更加 heavy 的 tails.
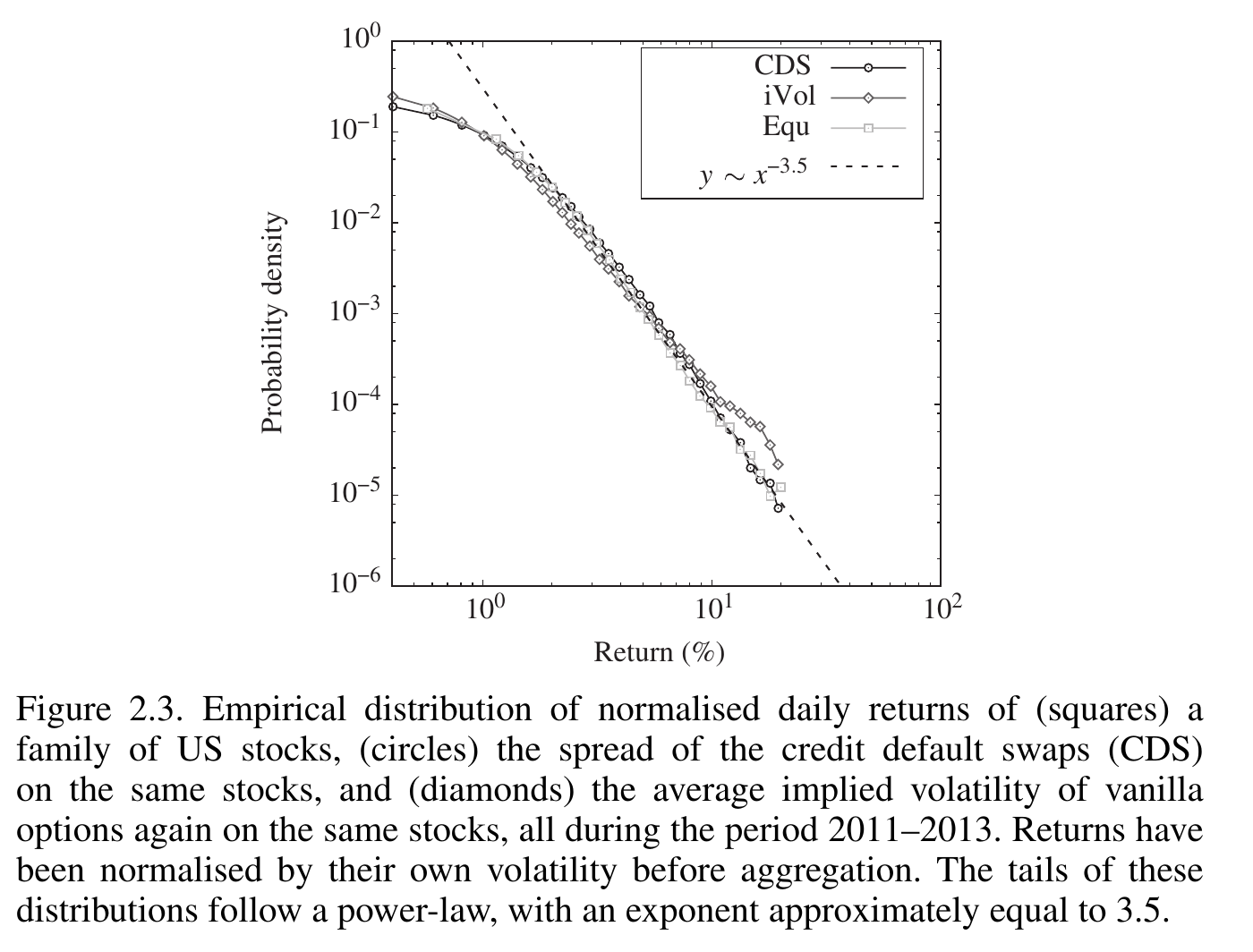
在较短的时间尺度上,unconditional return 的 empirical density function 可以用 stsudent's t distribution 较好地拟合,其 PDF 为:
$$f_r(r) = \dfrac{1}{\sqrt{\pi}} \dfrac{\Gamma[(1+\mu)/2]}{\Gamma[\mu/2]}\dfrac{a^\mu}{(r^2 + a^2)^{(1+\mu)/2}}$$其中
μ
\mu
μ 为 tail parameter,
a
a
a 则与 distribution 的 variance 有关:
σ
2
=
a
2
/
(
μ
−
2
)
\sigma^2 = a^2/(\mu - 2)
σ2=a2/(μ−2).
tail parameter
μ
\mu
μ 被发现一般在
3
3
3 附近。
当 ∣ r ∣ ≫ a |r| \gg a ∣r∣≫a 时, f r ( r ) → a μ ∣ r ∣ 1 + μ f_r(r) \to \dfrac{a^{\mu}}{|r|^{1+\mu}} fr(r)→∣r∣1+μaμ. 当 μ → ∞ \mu \to \infty μ→∞ 时,又变成了 Gaussian distribution.
Student's t distribution 的 tail 比 Gaussian 重得多,这意味着罕见事件并没有那么罕见。使用 Gaussian Distribution 会低估低概率事件的风险。
Volatility Clustering
我们说:returns 看上去几乎是 uncorrelated 的。但它们肯定不是 IID 的。
这里再次区分一下 uncorrelated 和 independence:uncorrelated 仅仅表明不存在线性关系,而 independence 则是不存在任何关系。
假如 return 是 IID 的,那么根据大数定律,在足够多的观察下,其 distribution 一定会向 Gaussian Distribution 收敛。但实际上 returns 几乎总是 non-Gaussian 的。
实际上,金融市场是高度 inermittent 的。有的时候市场很活跃,有的时候市场很冷清。volatility 本身也是一个 dynamic variable.
returns 可以被分解为一个与时间有关的 volatility 项 σ t \sigma_t σt 和一个 directional component ξ t \xi_t ξt:
$$r_t := \sigma_t \xi_t$$在这个表达中, ξ t \xi_t ξt 是具有 unit variance 的 IID random variable,也就是方向和大小是相对随机的。但 σ t \sigma_t σt 是一个正的波动率指标。 σ t \sigma_t σt 被发现具有 long memory.
令 σ t = σ 0 e ω t \sigma_t = \sigma_0 e^{\omega_t} σt=σ0eωt,其中 σ 0 \sigma_0 σ0 是设置 volatility scale 的常量, ω t \omega_t ωt 的 variogram 被发现可以用 Gaussian random variable 近似:
$$\mathcal{V}_\omega(\tau) = \left < (\omega_{t+\tau} - \omega_t)^2 \right > \approxeq \chi^2_0 \ln [1+\min(\tau,T)]$$其中 T T T 是一个很长的 cut-off time,一般以年为单位。 χ 0 \chi_0 χ0 设定了 log-volatility 波动的大小,经常被称为 volatility of the volatility(vol of vol). 对于大多数 assets, χ 0 2 ≊ 0.05 \chi^2_0 \approxeq 0.05 χ02≊0.05.
long memory 给出的 variogram 形式和 Ornstein-Uhlenbeck log-volatility process 听不一样的。后者使用一个 relaxation time τ ω \tau_\omega τω 刻画:
$$\mathcal{V}_\omega(\tau) = \chi^2_0 \left( 1 - e^{-\tau / \tau_\omega} \right)$$金融市场中的 volatility fluctuations 具有多重时间尺度。
volatility σ \sigma σ 和 scaled return ξ \xi ξ 并不是独立的,过去的正收益会减小未来的 volatility,而过去的负收益会增加未来的 volatility. 这被称为 leverage effect.
$$\tau >0, \left< \xi_t \sigma_{t+\tau} \right> <0$$ 但是过去的 volatility 基本上无法预测未来的 return sign: τ < 0 , < ξ t σ t + τ > ≊ 0 \tau < 0, \left< \xi_t \sigma_{t+\tau} \right> \approxeq 0 τ<0,⟨ξtσt+τ⟩≊0Activity Clustering
Market Activity 往往成堆出现。
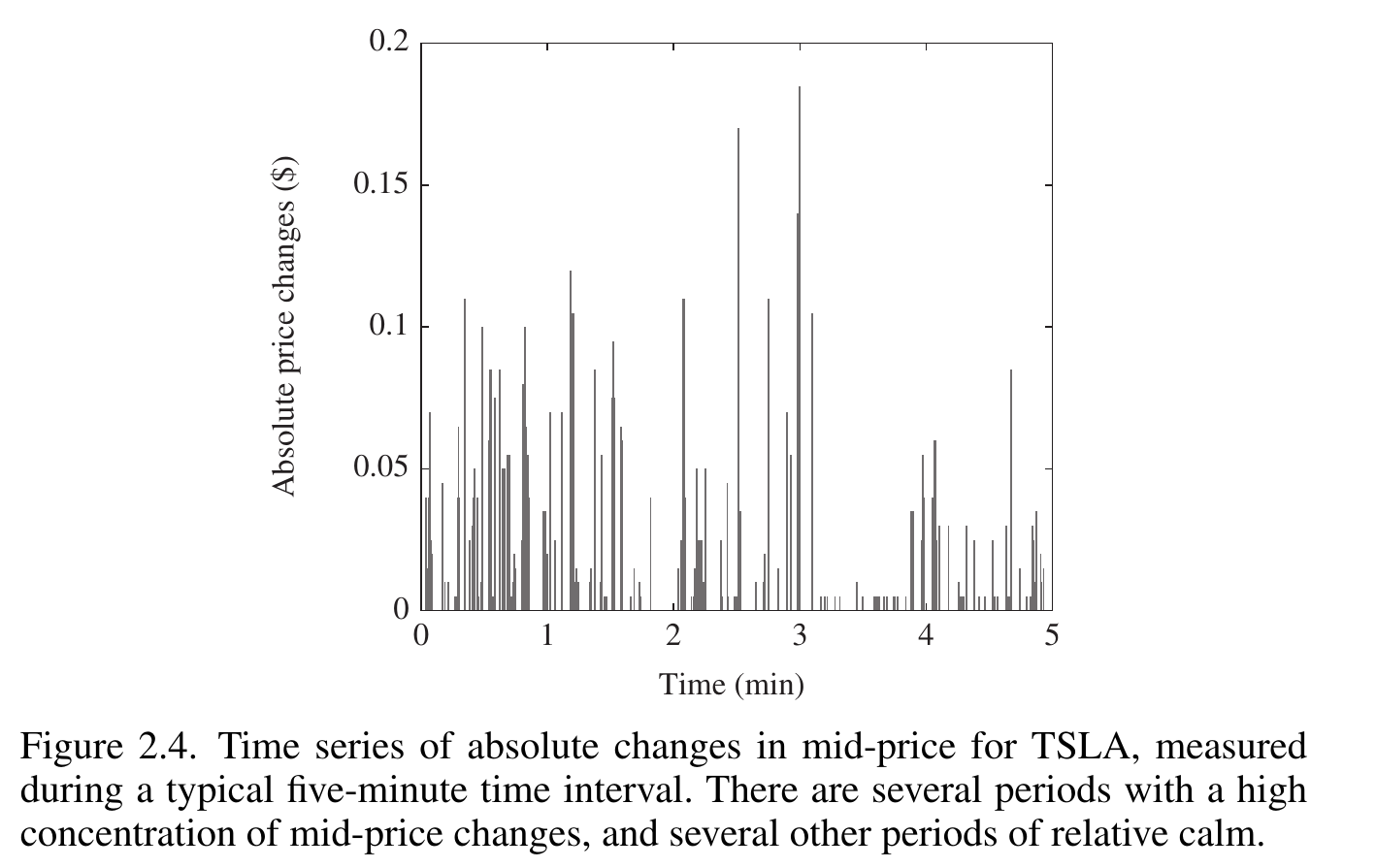
midprice change 都有这么强的 clustering 吗(
假设价格每次只能变动一个 tick θ \theta θ,每单位时间变动频率 φ \varphi φ,相应的 variance 就是:
σ 2 = φ θ 2 \sigma^2 = \varphi \theta^2 σ2=φθ2一个更精确的刻画是,选择一个时间 t t t 以及一小段时间 d t \mathrm{d} t dt,考察这段时间内 price changes 的数量 d N t \mathrm{d} N_t dNt,当 midprice 发生了变动 d N t = 1 \mathrm{d} N_t = 1 dNt=1,否则 d N t = 0 \mathrm{d} N_t=0 dNt=0. 由此可以得到平均市场活动 φ ‾ \overline{\varphi} φ 的定义:
< d N t > : = φ ‾ d t \left< \mathrm{d} N_t \right> := \overline{\varphi} \mathrm{d} t ⟨dNt⟩:=φdt其 covariance Cov [ d N t d t , d N t + τ d t ] \operatorname{Cov}\left[ \dfrac{\mathrm{d} N_t}{\mathrm{d}t}, \dfrac{\mathrm{d} N_{t+\tau}}{\mathrm{d}t} \right] Cov[dtdNt,dtdNt+τ] 刻画了市场波动的短期结构。
市场活动既由 long memory 影响,也由短期的波动影响。
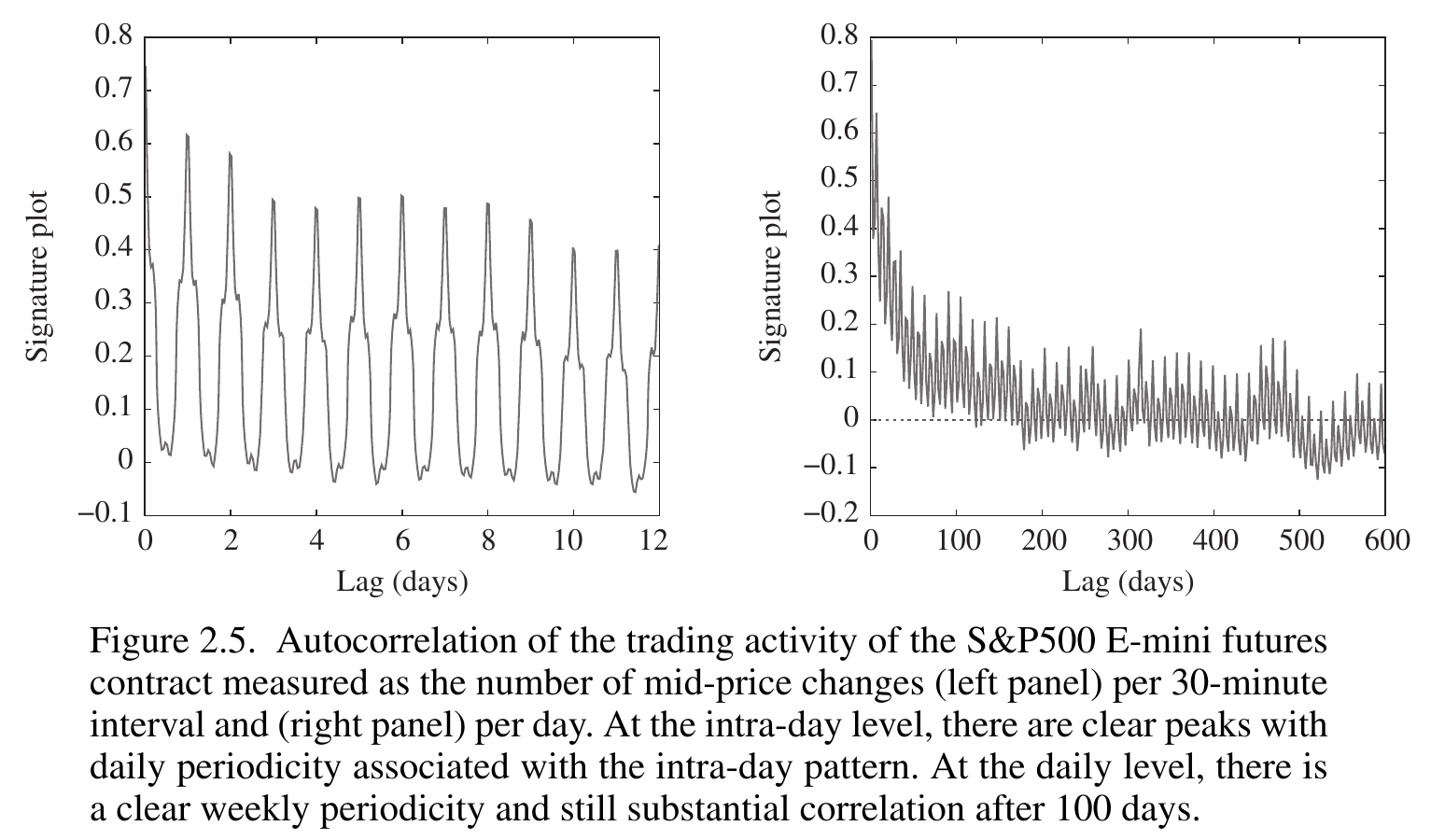
上面对市场价格变动的描述具有局限性。比如它无法刻画价格大部分时间稳定、但少数时间剧烈变动的情况。而实际市场中的价格往往具有两种波动:高频小波动和罕见的极端波动。
假设 return 遵循 Student's t distribution,那么在 4 σ 4\sigma 4σ 外的极端事件贡献了 30 % 30\% 30% 的 total variance,这是相当大的一部分波动。而且很多大变动实际上也跟 news 无关,似乎是市场自发涌现的特性。
这两种事件微妙地相互联系。在时间 t t t 增加的波动率,会倾向于在时间 t + τ t+\tau t+τ 引发更多的市场活动。比如说一个大的 price jump 往往跟随着一段市场活跃时间。似乎存在某种 self-excitation 的现象。
Why Do Prices Move?
为什么价格会变动?为什么会出现 random walks 的表现?
直觉地考虑, 市场价格似乎是这样变化的:
- 当某种 news 到来时,informed traders 参与买卖,使得价格快速移动以匹配其基本面。
- 随后,价格进行小幅度的、高频的波动,直到下一次 news 的到来。
但实际上,新闻的频率远远比大幅价格变动的频率低。大部分的 large price moves 似乎与 news 无关,而更像是交易活动的自发涌现。
这被称为 excess-volatility puzzle:实际上的波动率,和围绕 fundamental value 的波动相比,显著高得多。
此外,虽然消化 news 的影响、确定新的价格需要一段时间,金融市场似乎很少表现出 under-reaction(会创造趋势) 和 over-reaction(会创造 mean-reversion),使得 signalture plots 几乎是平的。
一个观点是,高度优化的执行算法和做市算法,积极地寻找 return series 中的 correlation 并加以利用。这些算法因而抹去了 signature plots 中的不规则部分。
高频算法从低频策略产生的 inefficiency 中获利,从而使 return 在任意时间尺度上都呈现出纯粹的随机性。
price efficiency 也有两种考察方式:
- fundamentally efficient:市场价格总是接近基本面。
- statistically efficient:在基于技术分析的交易行为中,任何可预测的模式都被完全利用。
根据 Black 的理论,fundamental values 的锚定效用只有在 random fluctuations σ T \sigma\sqrt{T} σT 的影响降低到至少 50% 的时候,才能在时间尺度 T T T 上观察到。对于 σ = 20 % \sigma= 20\% σ=20% 的 stock market,这需要六年的时间(?
怎么感觉这么奇怪。Whatever,这本书主要考察的是 statistical efficiency.
Overview
在各种时间尺度下,price changes 都是高度 uncorrelated 的。当然,uncorrelated 不代表 independence.
市场的交易活动会使价格自发涌现出各种表现,而并不一定依赖于外部的新闻。
quantitative volatility/activity feedback models(例如 ARCH-type models、hawkes process) 认为至少 80% 的 price variance 是由 self-referential effects 引起的。
这意味着大部分的价格变动都可以用市场本身的 microstructure view 来解释,而不依赖于宏观基本面分析。这些微观结构在各种各样的 liquidity market 都是类似的。
感觉还有很多内容没有消化,以后再回来看吧。
References to Read
-
Bachelier, L. (1900). Théorie de la spéculation. Gauthier-Villars.
- 提出 Random Walk Model 的最早论文。
-
Empirical properties of asset returns: stylized facts and statistical issues
- 简述了几条 stylized facts.
-
The distribution of realised stock return volatility
- 用于理解 return volatility 的一篇文章。
-
Volatility is rough
- 还是关于 volatility.
-
Power laws in economics and finance. Annual Review of Economics
-
On the correlation structure of microstructure noise: A financial economic approach.
-
The endogenous dynamics of markets: Price impact, feedback loops and instabilities.
-
Reconciling Efficient Markets with Behavioral Finance: The Adaptive Markets Hypothesis




















 4680
4680

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








