数据结构与算法 python--第五节 排序（七）堆排序

一、堆的概念

堆的结构可以分为大根堆和小根堆，是一个完全二叉树
完全二叉树：若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树

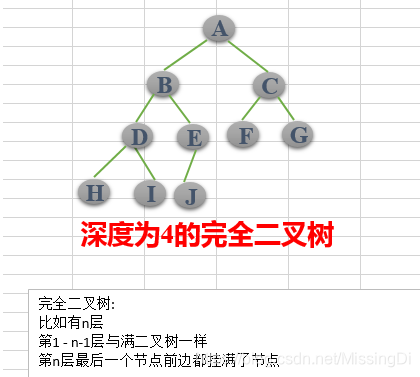
而堆排序是根据堆的这种数据结构设计的一种排序，下面先来看看什么是大根堆和小根堆

大根堆和小根堆

大根堆：每个结点的值都大于其左孩子和右孩子结点的值；
小根堆：每个结点的值都小于其左孩子和右孩子结点的值。
如下图

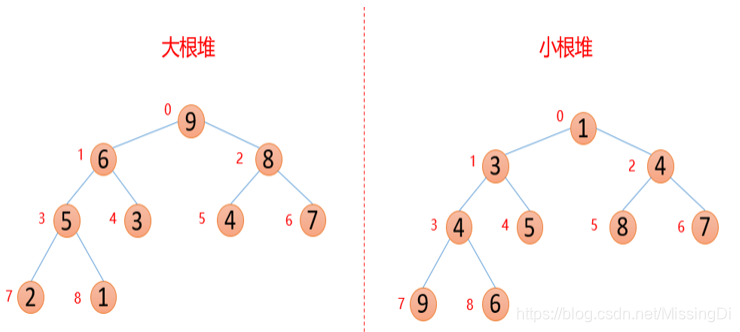
转换成数组即为：

对于数组中索引为 $i$ 的数，其父结点和左右孩子结点分别表示为：
父节点：$(i-1)//2$ （整除）
左子节点：$2\ast i+1$
右子节点：$2\ast I+2$

二 堆排序基本步骤

基本思想：

1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

2.1 构造堆

将无序数组的根节点及其子节点构造成一个大根堆

def heapify(tree,n,i):
    """将数组变换成 堆"""
#     n = len(tree)
    if i >= n:
        return
    l_c = 2*i + 1
    r_c = 2*i + 2
    max = i
    if l_c < n and tree[l_c] > tree[max]:
        max = l_c
    if r_c < n and tree[r_c] > tree[max]:
        max = r_c
    if max != i:
        tree[i],tree[max] = tree[max],tree[i]
        heapify(tree,n,max)

测试：

tree = [4,5,3,10,1,2]
n = 6
heapify(tree,n,0)

[5, 10, 3, 4, 1, 2]
此时，只对最上面的一个子树进行了 堆 的构造，实际上 需要对所有的节点都进行重新排列，故而进行下一步：
从树的最后一个叶子节点的父节点开始做heapify（如下图中的 3）

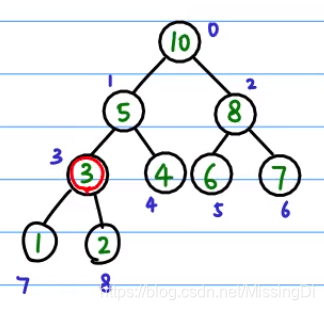
def build_heap(tree,n):
    last = n - 1
    parent = (last-1) // 2
    for i in range(parent,-1,-1):
        heapify(tree,n,i)

测试：

tree = [4,5,3,10,1,2]
n = 6
heapify(tree,n,0)
print(tree)
build_heap(tree,n)
print(tree)

[5, 10, 3, 4, 1, 2]
[10, 5, 3, 4, 1, 2]

最后一步：将堆顶端的数（最大）与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1；然后将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

def heap_sort(tree,n):
    build_heap(tree,n)
    for i in range(n-1,-1,-1): # for循环与while作用同，哪种表示都可以
#     i = n-1
#     while i >= 0:
        tree[i],tree[0] = tree[0],tree[i]
        heapify(tree,i,0)
#         i -= 1

测试：

tree = [4,5,3,10,1,2]
n = 6
heapify(tree,n,0)
print(tree)
build_heap(tree,n)
print(tree)
heap_sort(tree,n)
print(tree)

[5, 10, 3, 4, 1, 2]
[10, 5, 3, 4, 1, 2]
[1, 2, 3, 4, 5, 10]