读懂Ensemble，Bagging，Boosting以及Stacking

集成学习

• Bagging
  • 基于Bagging的Random Forest
• Boosting
  • 基于Boosting的AdaBGoost
  • Gradient Boosting Machines(GBM)梯度推进机
  • Gradient Boosted Regression Trees(GBRT)梯度提升回归树
• Stacking

Voting综述

Voting rule:

• Hard voting
• Soft voting

集成学习综述

集成学习归属于机器学习，它是一种训练思路，并不是某种具体的方法或者算法。 哲学思想为“三个臭皮匠赛过诸葛亮”。直观的理解就是，单个分类器的分类是可能出错的，不可靠的，但是如果多个分类器投票，那么可靠度就会高很多。

现实生活中，经常通过开会、投票等方法，以做出更加可靠的决策。集成学习就与此类似。集成学习就是有策略的生成一些基础模型，然后有策略地把它们都结合起来以做出最终的决策.

一般来说集成学习可以分为三类：

• 用于减少方差的bagging
• 用于减少偏差的boosting
• 用于提升预测结果的stacking

集成学习方法也可以归为如下两大类：

• 串行集成方法，这种方法串行地生成基础模型(AdaBoost)。串行集成的基本动机是利用基础模型之间的依赖。通过给错分样本一个较大的权重来提升性能。
• 并行集成方法，这种方法并行地生成基础模型(Random Forest).并行集成的基本动机就是利用基础模型的独立性，因为通过平均能够极大的降低误差。

Bagging综述

Bagging的思路是所有基础模型都一致对待，每个基础模型手里都只有一票，然后采用民主投票的方式得到最终的结果。

大部分情况下，经过bagging得到的结果方差(variance)更小。

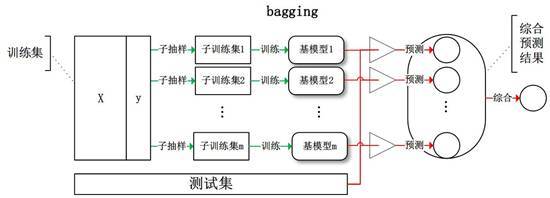
具体过程:

• 1.从原始样本集中抽取训练集。每轮从原始样本集中使用Boostrap的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行K轮抽取，得到K个训练集。（K个训练集之间是相互独立的）

• 2.每次使用一个训练集得到一个模型，K个训练集共得到K个模型。（注：这里并没有具体的分类算法或回归算法，我们可以根据具体问题采用不同的分类或回归方法，如决策树，感知器等）

• 3.对分类问题：将上步得到的K个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

举例：在bagging的方法中，最广为熟知的就是随机森林：bagging+决策树=随机森林

Boosting综述

Boosting和Bagging最本质的差别在于它对基础模型不是一致对待的，而是经过不停的考验和筛选来挑选出精英，然后给精英更多的投票权，表现不好的基础模型则给较少的投票权，然后综合所有人的投票得到最终的结果。

大部分情况下，经过boosting得到的结果偏差更小。

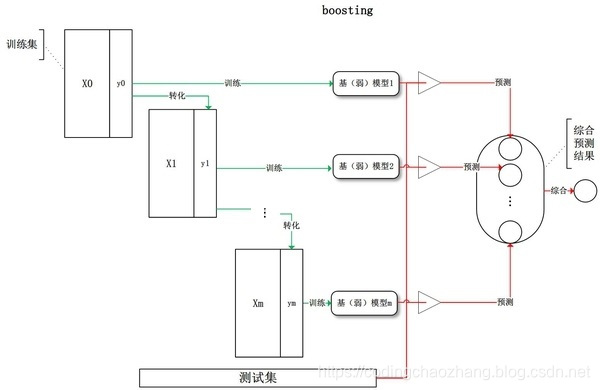
具体过程:

• 1.通过加法模型将基础模型进行线性的组合；
• 2.在每一轮训练都提升那些错误率小的基础模型权重，同时减小错误率高的模型权重；
• 3.在每一轮改变训练数据的权值或概率分布，通过提高那些在前一轮被弱分类器分错样例的权值，减少前一轮分队样例的权值，来使得分类器对误分的数据有较好的效果。

Stacking综述

将训练好的所有基础模型对整个训练集进行预测，第j个基模型对第i个训练样本的预测值将作为新的训练集中第i个样本的第j个特征值，最后基于新的训练集进行训练。同理，预测的过程也要先经过所有基模型的预测形成新的测试集，最后再对测试集进行预测。

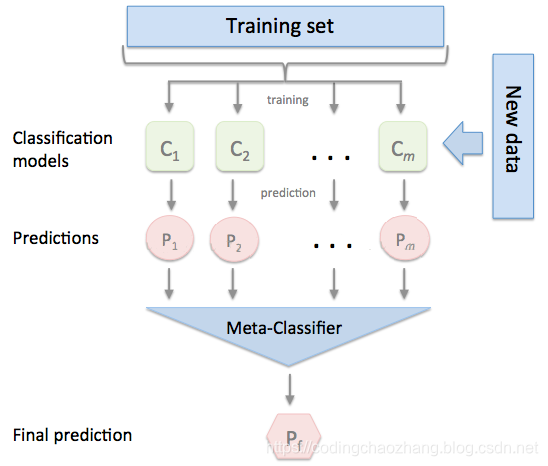
举例：

使用一款功能强大的stacking利器，mlxtend库，它可以很快地完成对sklearn模型的stacking。

• I. 最基本的使用方法，即使用前面分类器产生的特征输出作为最后总的meta-classifier的输入数据。

from sklearn import datasets
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingClassifier
import numpy as np
import warnings
warnings.filterwarnings("ignore")

iris = datasets.load_iris()

X,y = iris.data[:,1:3],iris.target

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=2019)
clf3 = GaussianNB()
lr = LogisticRegression()

sclf = StackingClassifier(classifiers=[clf1,clf2,clf3],meta_classifier=lr)

print("3-fold cross validation:\n")

for clf,label in zip([clf1,clf2,clf3,sclf],["KNN","Random Forest","Naive Bayes","StackingClassifier"]):
    scores = model_selection.cross_val_score(clf,X,y,cv=3,scoring="accuracy")
    print("Accuracy:%0.2f(+/-%0.2f)[%s]"%(scores.mean(),scores.std(),label))

3-fold cross validation:

Accuracy:0.91(+/-0.01)[KNN]
Accuracy:0.96(+/-0.03)[Random Forest]
Accuracy:0.92(+/-0.03)[Naive Bayes]
Accuracy:0.94(+/-0.03)[StackingClassifier]

• II. 另一种使用第一层基本分类器产生的类别概率值作为meta-classifier的输入，这种情况下需要将StackingClassifier的参数设置为use_probas=True.如果将参数设置为average_probas=True,那么这些基分类器对每一个类别产生的概率值会被平均，否则会拼接。

例如有两个基分类器产生的概率输出为：
classifier 1:[0.2,0.5,0.3]
classifier 2:[0.3,0.4,0.4]

若average为True，则产生的meta-feature为[0.25,0.45,0.35]；若average为False，产生的meta-feature为[0.2,0.5,0.3,0.3,0.4,0.4]

from sklearn import datasets
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingClassifier
import numpy as np
import warnings
warnings.filterwarnings("ignore")

iris = datasets.load_iris()
X,y = iris.data[:,1:3],iris.target

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=2019)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1,clf2,clf3],use_probas=True,average_probas=False,meta_classifier=lr)

print("3-fold cross validation:\n")

for clf,labl in zip([clf1,clf2,clf3,sclf],["KNN","Random Forest","Naive Bayes","StackingClassifier"]):
    scores = model_selection.cross_val_score(clf,X,y,cv=3,scoring="accuracy")
    print("Accuracy:%0.2f(+/-%0.2f)[%s]"%(scores.mean(),scores.std(),label))

3-fold cross validation:

Accuracy:0.91(+/-0.01)[StackingClassifier]
Accuracy:0.96(+/-0.03)[StackingClassifier]
Accuracy:0.92(+/-0.03)[StackingClassifier]
Accuracy:0.92(+/-0.02)[StackingClassifier]

• III. 另外一种方式是对训练集中的特征维度进行操作的，这次不是给每一个基分类器全部的特征，而是给不同的基分类器分不同的特征，即比如基分类器1训练前半部分特征，基分类器2训练后半部分的特征。最终通过StackingClassifier组合起来。

from sklearn.datasets import load_iris
from mlxtend.classifier import StackingClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression

iris = load_iris()
X = iris.data
y = iris.target

pipe1 = make_pipeline(ColumnSelector(cols=(0,2)),LogisticRegression())
pipe2 = make_pipeline(ColumnSelector(cols=(1,2,3)),LogisticRegression())

sclf = StackingClassifier(classifiers=[pipe1,pipe2],meta_classifier=LogisticRegression())

sclf.fit(X,y)

StackingClassifier(average_probas=False,
                   classifiers=[Pipeline(memory=None,
                                         steps=[('columnselector',
                                                 ColumnSelector(cols=(0, 2),
                                                                drop_axis=False)),
                                                ('logisticregression',
                                                 LogisticRegression(C=1.0,
                                                                    class_weight=None,
                                                                    dual=False,
                                                                    fit_intercept=True,
                                                                    intercept_scaling=1,
                                                                    l1_ratio=None,
                                                                    max_iter=100,
                                                                    multi_class='warn',
                                                                    n_jobs=None,
                                                                    penalty='l2',
                                                                    random_state=None,
                                                                    sol...
                   meta_classifier=LogisticRegression(C=1.0, class_weight=None,
                                                      dual=False,
                                                      fit_intercept=True,
                                                      intercept_scaling=1,
                                                      l1_ratio=None,
                                                      max_iter=100,
                                                      multi_class='warn',
                                                      n_jobs=None, penalty='l2',
                                                      random_state=None,
                                                      solver='warn', tol=0.0001,
                                                      verbose=0,
                                                      warm_start=False),
                   store_train_meta_features=False, use_clones=True,
                   use_features_in_secondary=False, use_probas=False,
                   verbose=0)

Bagging和Boosting的4点差别

• 样本选择上：

• Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮数据集之间是独立的。

• Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果 进行调整、

• 样例权重：

• Bagging：使用均匀采样，每个样例的权重相等。

• Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大

• 预测函数:

• Bagging：所有预测函数的权重相等。

• Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

• 并行计算：

• Bagging：每个预测函数可以并行生成

• Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

集成学习例子 Ensemble Methods

集成学习是将击中机器学习技术组合到一个预测模型的元算法，以此减少方差(Bagging),偏差(Boosting),或改善预测(Stacking).

集成方法可以分为两类：串行集成方法和并行集成方法。串行集成方法的基本动力是利用基础学习之间的依赖关系，因此可以通过对以前错误标记的示例进行加权来提高整体性能。并行方法的基本动机是利用基础学习之间的独立性，因此可以通过平均来减少错误。

为了使集成方法比任何单个成员更准确，基础学习必须尽可能准确且尽可能多样化。

Bagging

Bagging使用Bootstrap的抽样方法来获取数据集，以训练基础模型。为了汇总基础模型的输出，Bagging使用投票法进行分类，使用平均法进行回归。

%matplotlib inline

import itertools
import numpy as np

import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

from sklearn import datasets

from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier

from sklearn.ensemble import BaggingClassifier
from sklearn.model_selection import cross_val_score,train_test_split

from mlxtend.plotting import plot_learning_curves
from mlxtend.plotting import plot_decision_regions

np.random.seed(0)

import warnings
warnings.filterwarnings("ignore")

iris = datasets.load_iris()
X,y = iris.data[:,0:2],iris.target

clf1 = DecisionTreeClassifier(criterion="entropy",max_depth=1)
clf2 = KNeighborsClassifier(n_neighbors=1)

bagging1 = BaggingClassifier(base_estimator=clf1,n_estimators=10,max_samples=0.8,max_features=0.8)
bagging2 = BaggingClassifier(base_estimator=clf2,n_estimators=10,max_samples=0.8,max_features=0.8)

label = ["Decision Tree","K-NN","BaggingTree","Bagging K-NN"]
clf_list = [clf1,clf2,bagging1,bagging2]

fig = plt.figure(figsize=(10,8))
gs = gridspec.GridSpec(2,2)
grid = itertools.product([0,1],repeat=2)

for clf,label,grd in zip(clf_list,label,grid):
    scores = cross_val_score(clf,X,y,cv=3,scoring="accuracy")
    print("Accuracy:%.2f (+/- %.2f)[%s]"%(scores.mean(),scores.std(),label))
    
    clf.fit(X,y)
    ax = plt.subplot(gs[grd[0],grd[1]])
    fig = plot_decision_regions(X=X,y=y,clf=clf,legend=2)
    plt.title(label)
    
plt.show()

Accuracy:0.63 (+/- 0.02)[Decision Tree]
Accuracy:0.70 (+/- 0.02)[K-NN]
Accuracy:0.66 (+/- 0.02)[BaggingTree]
Accuracy:0.61 (+/- 0.02)[Bagging K-NN]

# plot learning curves
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=2019)

plt.figure()
plot_learning_curves(X_train,y_train,X_test,y_test,bagging1,print_model=False,style="ggplot")
plt.show()

#Ensemble Size
num_est = np.linspace(1,100,20).astype(int)
bg_clf_cv_mean = []
bg_clf_cv_std = []
for n_est in num_est:    
    bg_clf = BaggingClassifier(base_estimator=clf1, n_estimators=n_est, max_samples=0.8, max_features=0.8)
    scores = cross_val_score(bg_clf, X, y, cv=3, scoring='accuracy')
    bg_clf_cv_mean.append(scores.mean())
    bg_clf_cv_std.append(scores.std())

plt.figure()
(_, caps, _) = plt.errorbar(num_est, bg_clf_cv_mean, yerr=bg_clf_cv_std, c='blue', fmt='-o', capsize=5)
for cap in caps:
    cap.set_markeredgewidth(1)                                                                                                                                
plt.ylabel('Accuracy'); plt.xlabel('Ensemble Size'); plt.title('Bagging Tree Ensemble');
plt.show()

Boosting

Boosting是指能够将弱学习转换为强学习的一系列算法。

import itertools
import numpy as np

import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

from sklearn import datasets

from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression

from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import cross_val_score,train_test_split

from mlxtend.plotting import plot_learning_curves
from mlxtend.plotting import plot_decision_regions

iris = datasets.load_iris()
X,y = iris.data[:,0:2],iris.target

clf = DecisionTreeClassifier(criterion="entropy",max_depth=1)

num_est = [1,2,3,10]
label = ["AdaBoost(n_est=1)","AdaBoost(n_est=2)","AdaBoost(n_est=3)","AdaBoost(n_est=10)"]

fig = plt.figure(figsize=(10,8))
gs = gridspec.GridSpec(2,2)
grid = itertools.product([0,1],repeat=2)

for n_est,label,grd in zip(num_est,label,grid):
    boosting = AdaBoostClassifier(base_estimator=clf,n_estimators=n_est)
    boosting.fit(X,y)
    ax = plt.subplot(gs[grd[0],grd[1]])
    fig = plot_decision_regions(X=X,y=y,clf=boosting,legend=2)
    plt.title(label)
    
plt.show()

# plot learning curves
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=2019)

boosting = AdaBoostClassifier(base_estimator=clf,n_estimators=10)

plt.figure()
plot_learning_curves(X_train,y_train,X_test,y_test,boosting,print_model=False,style="ggplot")
plt.show()

#Ensemble Size
num_est = np.linspace(1,100,20).astype(int)
bg_clf_cv_mean = []
bg_clf_cv_std = []
for n_est in num_est:    
    ada_clf = AdaBoostClassifier(base_estimator=clf, n_estimators=n_est)
    scores = cross_val_score(ada_clf, X, y, cv=3, scoring='accuracy')
    bg_clf_cv_mean.append(scores.mean())
    bg_clf_cv_std.append(scores.std())

plt.figure()
(_, caps, _) = plt.errorbar(num_est, bg_clf_cv_mean, yerr=bg_clf_cv_std, c='blue', fmt='-o', capsize=5)
for cap in caps:
    cap.set_markeredgewidth(1)                                                                                                                                
plt.ylabel('Accuracy'); plt.xlabel('Ensemble Size'); plt.title('AdaBoost Ensemble');
plt.show()

Stacking

Stacking是一种集成学习技术，可通过元分类器或元回归器组合多个分类或回归模型。

示例1 简单堆叠分类

from sklearn import datasets

iris = datasets.load_iris()
X,y = iris.data[:,1:3],iris.target

from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingClassifier
import numpy as np

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=2019)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1,clf2,clf3],meta_classifier=lr)

print("3-fold cross validation:\n")

for clf,label in zip([clf1,clf2,clf3,sclf],["KNN","Random Forest","Navie Bayes","Stacking Classifier"]):
    scores = model_selection.cross_val_score(clf,X,y,cv=3,scoring="accuracy")
    print("Accuracy:%0.2f(+/-%0.2f)[%s]"%(scores.mean(),scores.std(),label))

3-fold cross validation:

Accuracy:0.91(+/-0.01)[KNN]
Accuracy:0.96(+/-0.03)[Random Forest]
Accuracy:0.92(+/-0.03)[Navie Bayes]
Accuracy:0.94(+/-0.03)[Stacking Classifier]

import matplotlib.pyplot as plt
from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
import itertools

gs = gridspec.GridSpec(2,2)

fig = plt.figure(figsize=(10,8))

for clf,lab,grd in zip([clf1,clf2,clf3,sclf],["KNN","Random Forest","Naive Bayes","Stacking Classifier"],itertools.product([0,1],repeat=2)):
    clf.fit(X,y)
    ax = plt.subplot(gs[grd[0],grd[1]])
    fig = plot_decision_regions(X=X,y=y,clf=clf)
    plt.title(lab)

示例2 使用概率作为元特征

或者，可以通过设置使用第一级分类器的类概率来训练元分类器（第二级分类器）use_probas=True。如果为average_probas=True，则对第1级分类器average_probas=False的概率进行平均，如果为，则将这些概率进行堆叠（推荐）。例如，在具有2个1级分类器的3级设置中，这些分类器可以对1个训练样本做出以下“概率”预测：

• 分类器1：[0.2、0.5、0.3]
• 分类器2：[0.3、0.4、0.4]

如果为average_probas=True，则元功能将为：

• [0.25，0.45，0.35]

相反，average_probas=False通过堆叠以下1级概率，在k个特征中使用结果，其中k = [n_classes * n_classifiers]：

• [0.2、0.5、0.3、0.3、0.4、0.4]

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3],
                          use_probas=True,
                          average_probas=False,
                          meta_classifier=lr)

print('3-fold cross validation:\n')

for clf, label in zip([clf1, clf2, clf3, sclf], ['KNN', 'Random Forest',  'Naive Bayes','StackingClassifier']):
    scores = model_selection.cross_val_score(clf, X, y, cv=3, scoring='accuracy')
    print("Accuracy: %0.2f (+/- %0.2f) [%s]"  % (scores.mean(), scores.std(), label))

3-fold cross validation:

Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.93 (+/- 0.05) [Random Forest]
Accuracy: 0.92 (+/- 0.03) [Naive Bayes]
Accuracy: 0.94 (+/- 0.03) [StackingClassifier]

示例3 堆叠分类和GridSearch

堆栈允许调整基本模型和元模型的超级参数！可通过来获得可调参数的完整列表estimator.get_params().keys()。

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB 
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from mlxtend.classifier import StackingClassifier

# Initializing models

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3], meta_classifier=lr)

params = {'kneighborsclassifier__n_neighbors': [1, 5], 'randomforestclassifier__n_estimators': [10, 50], 'meta_classifier__C': [0.1, 10.0]}

grid = GridSearchCV(estimator=sclf, param_grid=params, cv=5,refit=True)
grid.fit(X, y)

cv_keys = ('mean_test_score', 'std_test_score', 'params')

for r, _ in enumerate(grid.cv_results_['mean_test_score']):
    print("%0.3f +/- %0.2f %r" % (grid.cv_results_[cv_keys[0]][r],grid.cv_results_[cv_keys[1]][r] / 2.0,grid.cv_results_[cv_keys[2]][r]))

print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)

0.667 +/- 0.00 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.667 +/- 0.00 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.927 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.920 +/- 0.03 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.667 +/- 0.00 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.667 +/- 0.00 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.933 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.940 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
Best parameters: {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
Accuracy: 0.94

如果我们计划多次使用回归算法，我们要做的就是在参数网格中添加一个附加的数字后缀，如下所示：

from sklearn.model_selection import GridSearchCV

# Initializing models

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf1, clf2, clf3], 
                          meta_classifier=lr)

params = {'kneighborsclassifier-1__n_neighbors': [1, 5], 'kneighborsclassifier-2__n_neighbors': [1, 5], 'randomforestclassifier__n_estimators': [10, 50],  'meta_classifier__C': [0.1, 10.0]}

grid = GridSearchCV(estimator=sclf, param_grid=params,cv=5,refit=True)
grid.fit(X, y)

cv_keys = ('mean_test_score', 'std_test_score', 'params')

for r, _ in enumerate(grid.cv_results_['mean_test_score']):
    print("%0.3f +/- %0.2f %r" % (grid.cv_results_[cv_keys[0]][r],grid.cv_results_[cv_keys[1]][r] / 2.0,grid.cv_results_[cv_keys[2]][r]))

print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)

0.667 +/- 0.00 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.667 +/- 0.00 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.907 +/- 0.03 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.920 +/- 0.03 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.667 +/- 0.00 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.667 +/- 0.00 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.927 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.920 +/- 0.03 {'kneighborsclassifier-1__n_neighbors': 1, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.667 +/- 0.00 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.667 +/- 0.00 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.927 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.920 +/- 0.03 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.667 +/- 0.00 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.667 +/- 0.00 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.933 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.940 +/- 0.02 {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
Best parameters: {'kneighborsclassifier-1__n_neighbors': 5, 'kneighborsclassifier-2__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
Accuracy: 0.94

该StackingClassifier还能够通过网格搜索classifiers参数。当存在级别混合的超参数时，GridSearchCV将尝试以自上而下的顺序替换超参数，即分类器->单基分类器->分类器超参数。例如，给定一个超参数网格，例如

params = {'randomforestclassifier__n_estimators': [1, 100],
'classifiers': [(clf1, clf1, clf1), (clf2, clf3)]}

它将首先使用（clf1，clf1，clf1）或（clf2，clf3）的实例设置。然后它将替换'n_estimators'基于的匹配分类器的设置'randomforestclassifier__n_estimators': [1, 100]。

示例4：在不同特征子集上运行的分类器的堆叠

不同的1级分类器可以适合训练数据集中的不同特征子集。以下示例说明了如何使用scikit-learn管道和ColumnSelector：在技术层面上做到这一点：

from sklearn.datasets import load_iris
from mlxtend.classifier import StackingClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression

iris = load_iris()
X = iris.data
y = iris.target

pipe1 = make_pipeline(ColumnSelector(cols=(0, 2)),
                      LogisticRegression())
pipe2 = make_pipeline(ColumnSelector(cols=(1, 2, 3)),
                      LogisticRegression())

sclf = StackingClassifier(classifiers=[pipe1, pipe2], 
                          meta_classifier=LogisticRegression())

sclf.fit(X, y)

StackingClassifier(average_probas=False,
                   classifiers=[Pipeline(memory=None,
                                         steps=[('columnselector',
                                                 ColumnSelector(cols=(0, 2),
                                                                drop_axis=False)),
                                                ('logisticregression',
                                                 LogisticRegression(C=1.0,
                                                                    class_weight=None,
                                                                    dual=False,
                                                                    fit_intercept=True,
                                                                    intercept_scaling=1,
                                                                    l1_ratio=None,
                                                                    max_iter=100,
                                                                    multi_class='warn',
                                                                    n_jobs=None,
                                                                    penalty='l2',
                                                                    random_state=None,
                                                                    sol...
                   meta_classifier=LogisticRegression(C=1.0, class_weight=None,
                                                      dual=False,
                                                      fit_intercept=True,
                                                      intercept_scaling=1,
                                                      l1_ratio=None,
                                                      max_iter=100,
                                                      multi_class='warn',
                                                      n_jobs=None, penalty='l2',
                                                      random_state=None,
                                                      solver='warn', tol=0.0001,
                                                      verbose=0,
                                                      warm_start=False),
                   store_train_meta_features=False, use_clones=True,
                   use_features_in_secondary=False, use_probas=False,
                   verbose=0)