RBtree红黑树(含代码与解释)

红黑树原理与实现详解

原创已于 2025-10-06 13:17:33 修改 · 544 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

于 2025-10-06 13:17:03 首次发布

一、什么是红黑树

红黑树的定义

红黑树是一种自平衡的二叉搜索树，通过颜色标记和旋转操作确保树的高度始终保持在O(log n)范围内，从而保证插入、删除、查找等操作的高效性。

核心特性

每个节点非红即黑，根节点为黑。
红色节点的子节点必须为黑（无连续红节点）。
从任一节点到其叶子节点的路径包含相同数量的黑节点（黑高平衡）。//建议多看几遍这是核心

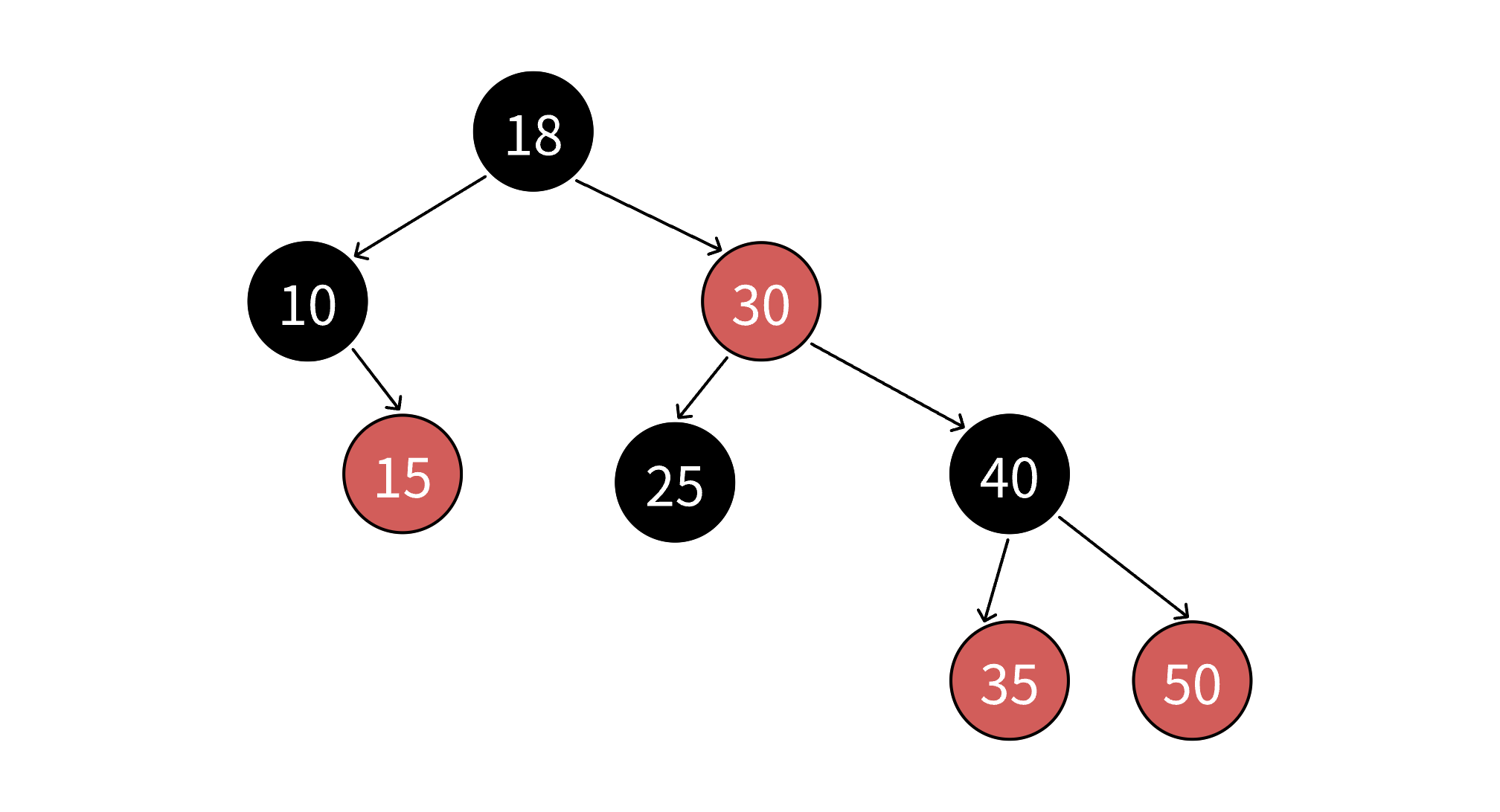
由此保证高度差永远是小于等于最短路径的二倍的

二、如何变色

我们可以把一颗红黑树抽象的表述为：

g 祖宗

p u 父亲舅舅

c 要插入的孩子

由红黑树规则可知一个正常的红黑树c一定为红色（插入黑色会严重破坏树的结构），所以说如果父亲是黑色的直接插入即可什么都不用管；if（p->_color == black）

若父亲是红色那祖宗g必然是黑色此时的变量就只有u舅舅了；else

现在我们讨论舅舅的情况分为三种没有舅舅，舅舅是黑色的，舅舅是红色的；

2.1直接变色

我直接告诉答案：没有舅舅和舅舅是黑色的情况归位一类变化相同；此时情况就是：

{if（舅舅是红色的）{} else{}；}

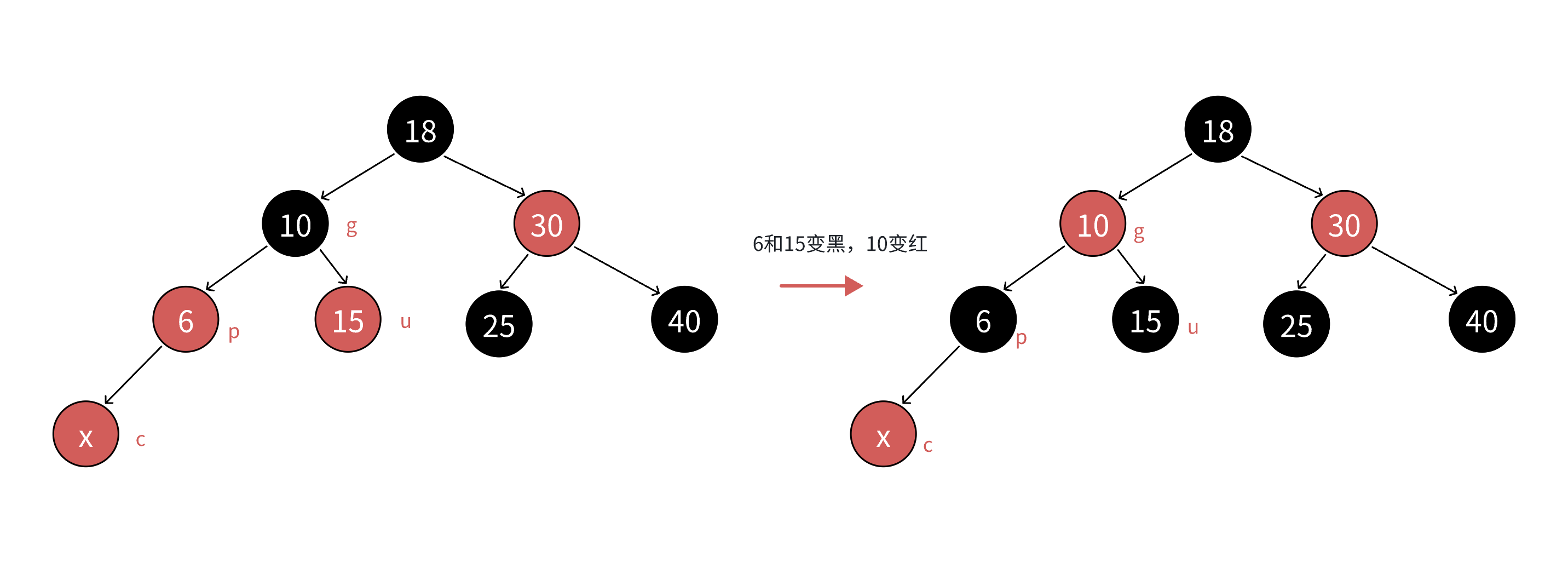
如图所示舅舅是红色的时候直接变色，让g变红，pu变黑就行了；

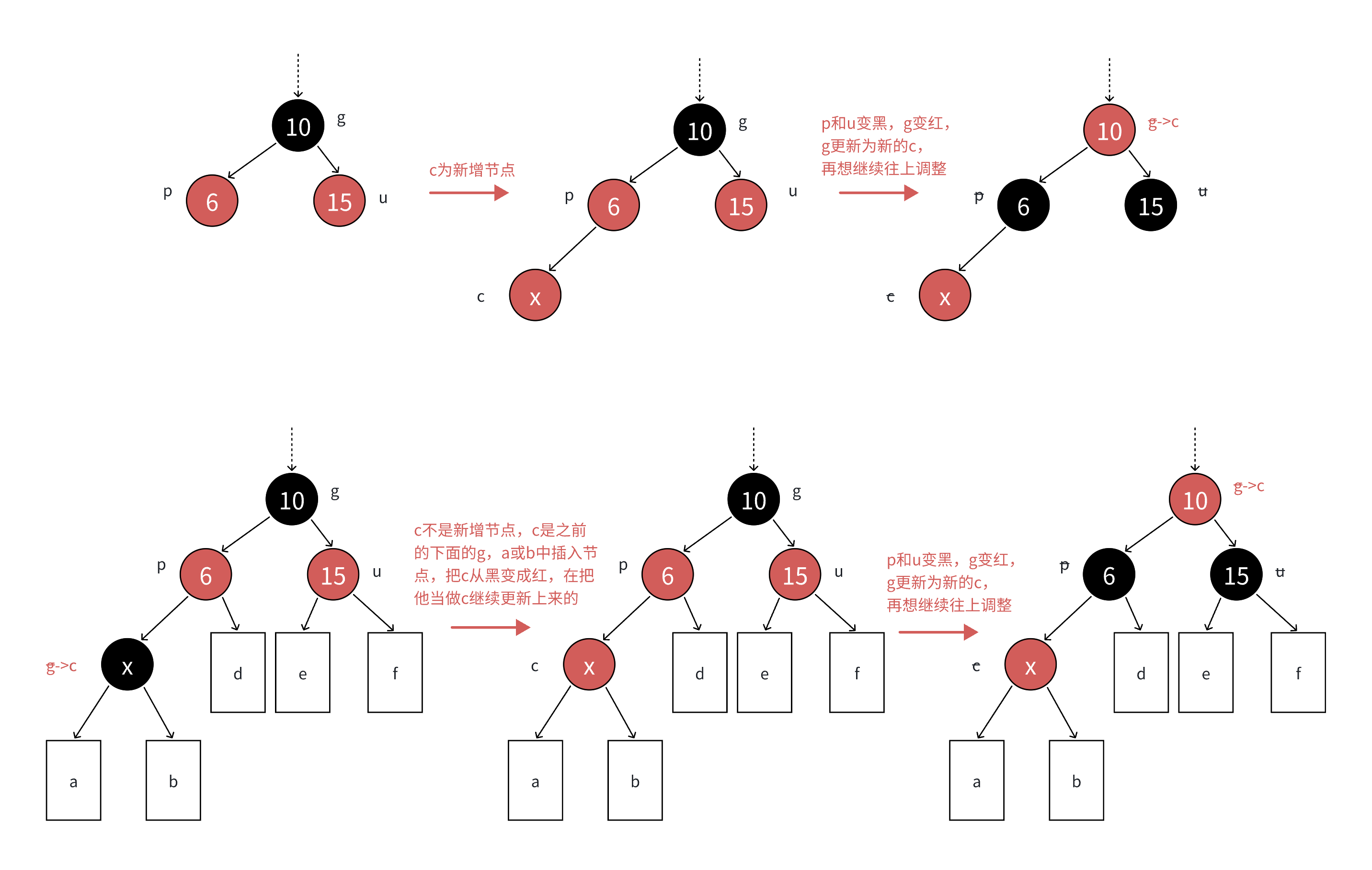
由上图可知在插入后变化可能会影响到上一级，在逐步向上是c可能不是新插入的结点而由新插入结点的祖宗g变过来的此时就需要逐级继续据徐变色while（c）；

2.2旋转加变色

麻烦的是else（舅舅是黑色或者没有）

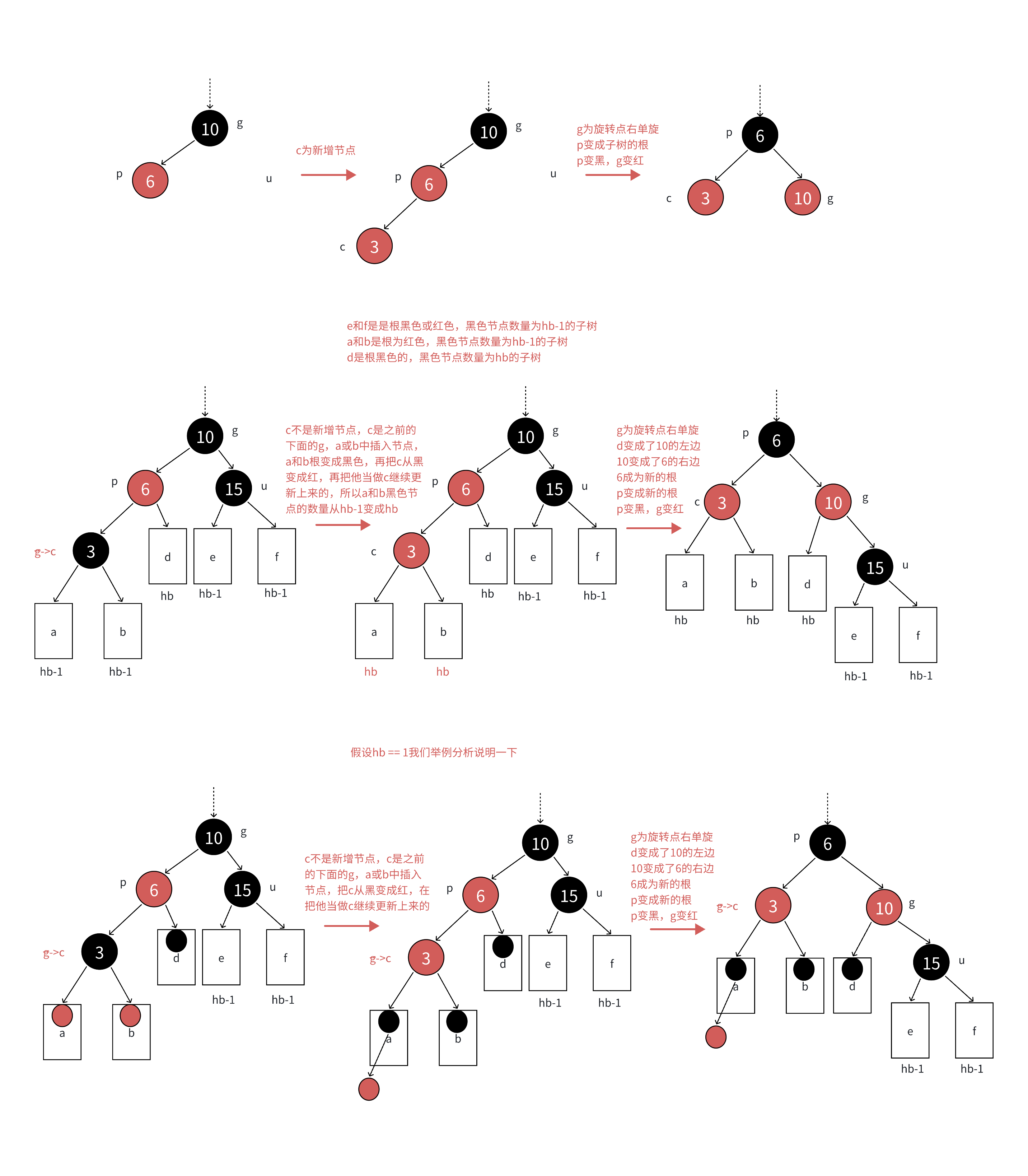
当没有舅舅或舅舅是黑色，我们只需要先判断舅舅是在祖宗的左还是右如果舅舅在右边，在继续判断新插入或变上来的新红色结点是在p父亲的左还是右就行，那p就是右旋转反之亦然；特殊情况：

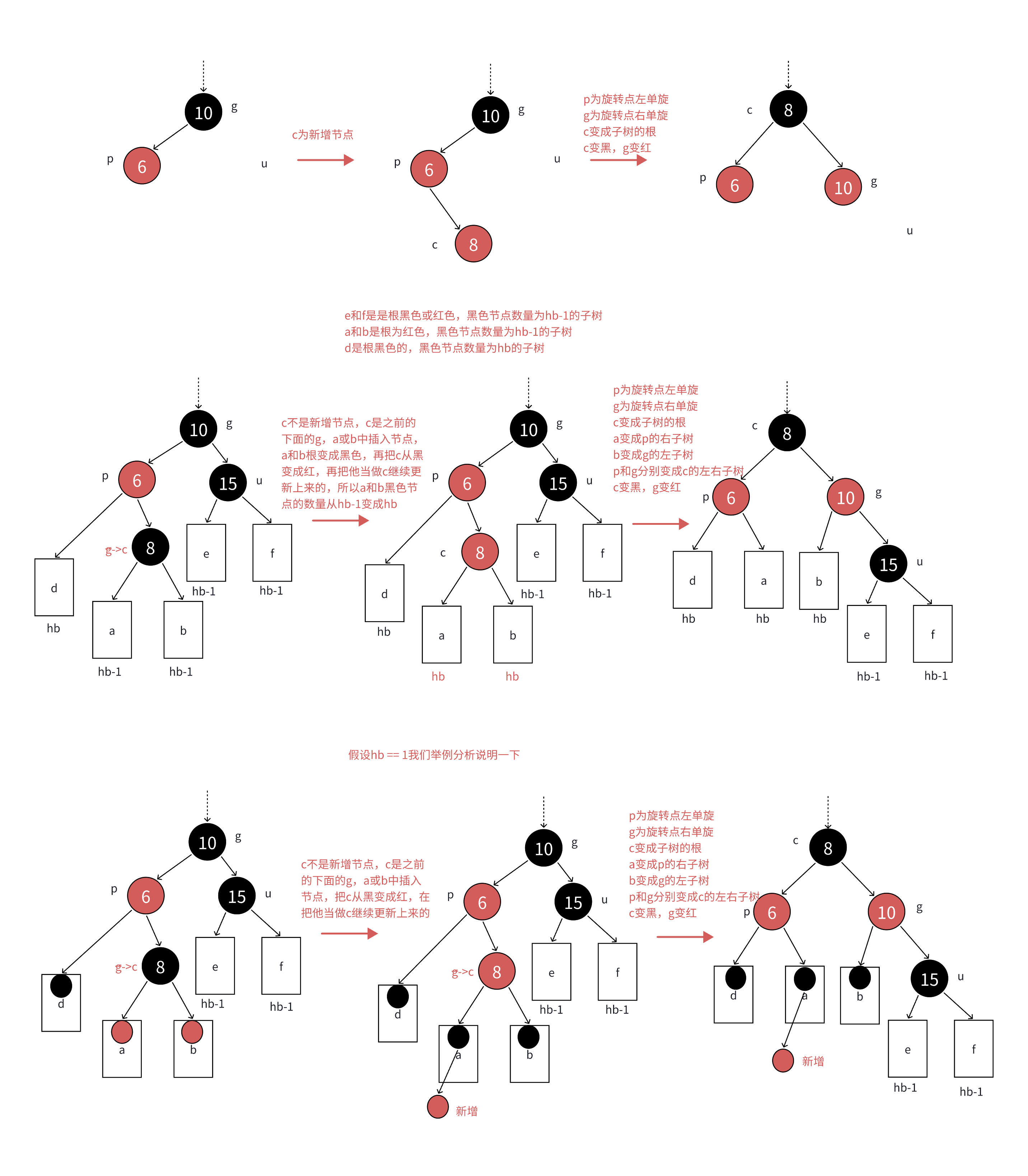
g和p和c不在同一条方向上此时需要进行双旋，以（舅舅在右边的情况为例子）先把p左旋转，再把旋转上来的c进行右旋转；之后c变黑色，g变红；

三、代码加注释

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
enum color
{
	RED,
	BLACK
};
template<class K, class T>
struct pair
{
	K _first;
	T _second;
	pair(K key, T val)
	{
		_first = key;
		_second = val;
	}
};//与map里的pair类似；
template<class K, class T>
struct RBtreeNode
{

	pair<K, T>* _kt;
	RBtreeNode<K, T>* _left = nullptr;
	RBtreeNode<K, T>* _right = nullptr;
	RBtreeNode* _parent = nullptr;
	color _col;
	RBtreeNode(K key, T val)
	{

		_kt = new pair<K, T>(key, val);
		_left = nullptr;
		_right = nullptr;
		_parent = nullptr;
		
	}


};//RB树的结点
template<class K, class T>
class RBtree
{
public:
	RBtree()
	{
		_root = nullptr;
	}
	typedef RBtreeNode<K, T> node;
	void insert(const K& key, const T& val)
	{

		if (_root == nullptr)
		{
			_root = new node(key, val);
			_root->_col = BLACK;
		}//根空则先给根；
		else
		{

			node* parent = nullptr;
			node* cur = _root;
			while (cur) {
				if (cur->_kt->_first > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else//(cur->_kt->_first < key)
				{
					parent = cur;
					cur = cur->_right;

				}
			}//寻找插入点小的左子树大的右子树；
			cur = new node(key, val);
			if (parent->_kt->_first > cur->_kt->_first)
			{
				parent->_left = cur;
				cur->_parent = parent;
				
			}
			else
			{
				parent->_right = cur;
				cur->_parent = parent;

			}
			cur->_col = RED;//插入之后再看变不变色；注意新插入的结点颜色固定为红；
			node* ground = parent->_parent;
			node* jojo = nullptr;//舅舅
			while (cur != _root)
			{
				if (ground == nullptr)//如果父亲就是根直接插入不用管了
				{
					break;
				}
				else//如果父亲不是根分情况
				{

					if (ground->_left == parent)
					{
						jojo = ground->_right;
					}
					else
					{
						jojo = ground->_left;

					}//找到舅舅也就是祖父除父亲外的另一个孩子

					if (parent->_col == BLACK)
					{
						break;
					}//要是父亲是黑色的也直接插入就完事
					else
					{
						if (jojo && jojo->_col == RED)
						{
							parent->_col = BLACK;
							jojo->_col = BLACK;
							ground->_col = RED;
							if (ground == _root)
							{
								ground->_col = BLACK;
								break;
							}
							cur = ground;
							parent = ground->_parent;
							ground = parent->_parent;//之后在向上变化;

						}//此时父亲和舅舅颜色都是红色那么我们直接把祖父颜色改成红色，父亲和舅舅改成黑色，就符合规则了；注意祖父是根的情况；
						else//此时舅舅颜色是黑色或者没有舅舅
						{
							if (ground->_right == jojo)//舅舅在右侧
							{
								if (parent->_left == cur)
								{

									xuanR(ground);
									parent->_col = BLACK;
									ground->_col = RED;

									//右单旋变色
								}
								else
								{
									xuanLR(parent);
									cur->_col = BLACK;
									ground->_col = RED;
									//左右双旋变色；
								}
							}
							else
							{
								if (parent->_right == cur)
								{

									xuanL(ground);
									parent->_col = BLACK;
									ground->_col = RED;
									//左单旋变色
								}
								else
								{
									xuanRL(parent);
									cur->_col = BLACK;
									ground->_col = RED;

									//左右双旋变色；
								}

							}
							break;
						}



					}

				}
			}
		}
	}
	void xuanR(node* parent)
	{
		
			node* subL = parent->_left;
			node* subLR = subL->_right;
			subL->_right = parent;
			parent->_left = subLR;
			if (subLR)
				subLR->_parent = parent;

			if (parent == _root)
			{
				subL->_parent = nullptr;
				parent->_parent = subL;
				_root = subL;
			}
			else
			{
				subL->_parent = parent->_parent;
				if (parent->_parent->_left == parent)
				{
					parent->_parent->_left = subL;
				}
				else
				{
					parent->_parent->_right = subL;
				}
				parent->_parent = subL;
			}

		
	}
	void xuanL(node* parent)
	{
		
			node* subR = parent->_right;
			node* subRL = subR->_left;
			subR->_left = parent;
			parent->_right = subRL;
			if (subRL)
				subRL->_parent = parent;

			if (parent == _root)
			{
				subR->_parent = nullptr;
				parent->_parent = subR;
				_root = subR;
			}
			else
			{
				subR->_parent = parent->_parent;
				if (parent->_parent->_left == parent)
				{
					parent->_parent->_left = subR;
				}
				else
				{
					parent->_parent->_right = subR;
				}
				parent->_parent = subR;
			}
		
	}

	void xuanLR(node* parent)
	{
		node* ground = parent->_parent;
		xuanL(parent);
		xuanR(ground);
		
	}
	void  xuanRL(node* parent)
	{
		node* ground = parent->_parent;
		xuanR(parent);
		xuanL(ground);
	}
	bool check()
	{
		if (this->_root->_col == RED)
		{
			return false;
		}
		int n = 0;
		return blacknum(this->_root, 0, n);
	}//检查
	bool blacknum(node* root,int b,int& n)//b遇见黑色结点就+1；n再遍历一个路径后以这一个路径为黑色结点基础与其他路径的b进行比较；
	{
		if (root == nullptr)
		{
			if (n == 0)
			{
				n = b;
			}

			if (b != n)
			{
				return false;
			}
			return true;
	     }

		if (root->_col == BLACK)
		{
			b++;
		}
		else
		{
			if (root->_parent&& root->_parent->_col==RED )
			{
				return false;
			}
		}
		blacknum(root->_left,b,n);
		std::cout << root->_kt->_first<<" ";
		blacknum(root->_right,b,n);
		return true;
	}//检查黑色结点数量是否每一路径都相等；
private:
	node* _root = nullptr;
};
int main()
{
	RBtree<int, int> a;
	int i[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	for (auto e : i)
	{
		a.insert(e, e);
	}



	std::cout << std::endl<< a.check() << std::endl;
	int b = 0;



}

再提一嘴在检查黑色结点个数的时候传进去的b是临时变量所以不会被保存下来而n用了引用所以会被保留以作为基准；