原因总结:
- MSE 会有梯度消失现象
- MSE 的导数非凸函数,求解最优解困难
证明:
1. 梯度消失公式证明:
令 ,记为
。
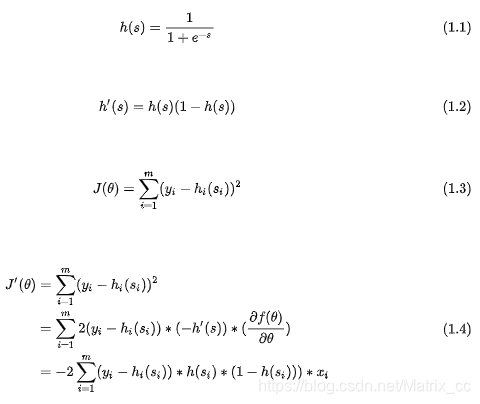
只关注其中单项的公式,并简化可得:
![]()
可见, 当 h 趋近于 0 时或者趋近于 1 时,该 Loss 的导数都会趋近为 0,从而造成梯度消失现象。
2. 非凸函数公式证明
关注 其二阶导数,可以得出其二阶导数矩阵即 Hessian 矩阵不是正定矩阵。 该导数是非凸函数,不是凸函数,难以优化。
证明:
令 ,记为
。
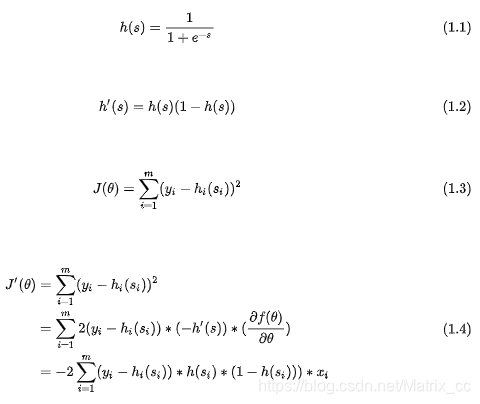
只关注其中单项的公式,并简化可得:
![]()
可见, 当 h 趋近于 0 时或者趋近于 1 时,该 Loss 的导数都会趋近为 0,从而造成梯度消失现象。
关注 其二阶导数,可以得出其二阶导数矩阵即 Hessian 矩阵不是正定矩阵。 该导数是非凸函数,不是凸函数,难以优化。

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


