【图像识别】基于LBP+LPQ算法融合人脸表情识别matlab源码

LBP与LPQ特征提取

最新推荐文章于 2025-12-05 14:37:41 发布

原创最新推荐文章于 2025-12-05 14:37:41 发布 · 84 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #matlab #计算机视觉 #人工智能 #图像处理

　LBP(Local Binary Pattern，局部二值模式)是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征；

1、LBP特征的描述

　　原始的LBP算子定义为在3*3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数(通常转换为十进制数即LBP码，共256种)，即得到该窗口中心像素点的LBP值，并用这个值来反映该区域的纹理信息。如下图所示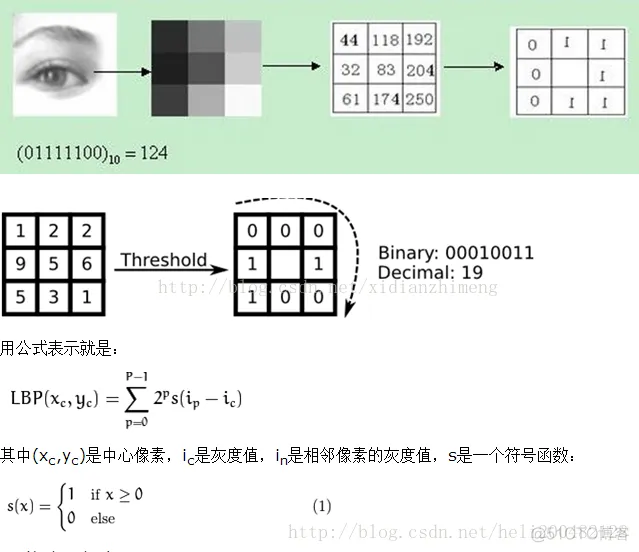：【图像识别】基于LBP+LPQ算法融合人脸表情识别matlab源码_图像处理

LBP的改进版本：

　　原始的LBP提出后，研究人员不断对其提出了各种改进和优化。

(1)圆形LBP算子：

　　基本的 LBP 算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala 等对 LBP 算子进行了改进，将 3×3 邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子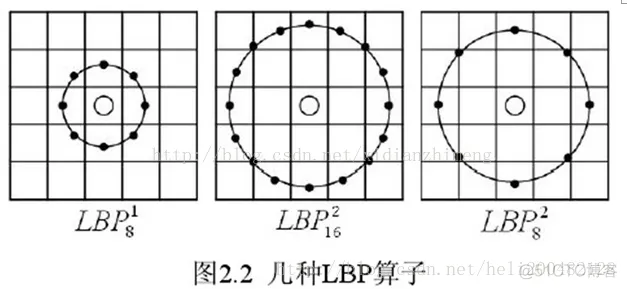；【图像识别】基于LBP+LPQ算法融合人脸表情识别matlab源码_matlab_02

(2)LBP旋转不变模式

　　从 LBP 的定义可以看出，LBP 算子是灰度不变的，但却不是旋转不变的。图像的旋转就会得到不同的 LBP值。
　　Maenpaa等人又将 LBP 算子进行了扩展，提出了具有旋转不变性的 LBP 算子，即不断旋转圆形邻域得到一系列初始定义的 LBP 值，取其最小值作为该邻域的 LBP 值。
　　图 2.5 给出了求取旋转不变的 LBP 的过程示意图，图中算子下方的数字表示该算子对应的 LBP 值，图中所示的 8 种 LBP模式，经过旋转不变的处理，最终得到的具有旋转不变性的 LBP 值为 15。也就是说，图中的 8 种 LBP 模式对应的旋转不变的 LBP 模式都是00001111。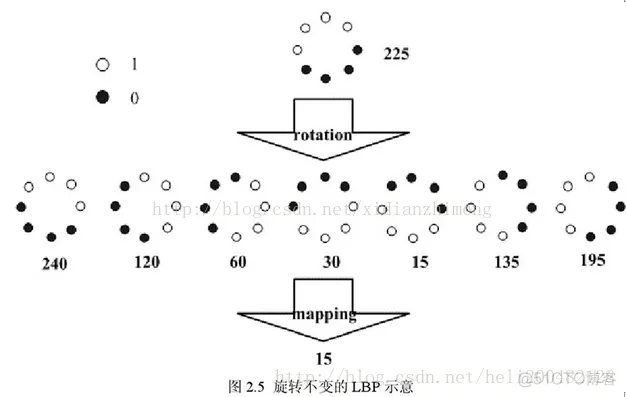【图像识别】基于LBP+LPQ算法融合人脸表情识别matlab源码_matlab_03

(3)LBP等价模式

　　一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生2P2P种模式。很显然，随着邻域集内采样点数的增加，二进制模式的种类是急剧增加的。例如：5×5邻域内20个采样点，有220220＝1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。同时，过多的模式种类对于纹理的表达是不利的。例如，将LBP算子用于纹理分类或人脸识别时，常采用LBP模式的统计直方图来表达图像的信息，而较多的模式种类将使得数据量过大，且直方图过于稀疏。因此，需要对原始的LBP模式进行降维，使得数据量减少的情况下能最好的代表图像的信息。
　　为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”(Uniform Pattern)来对LBP算子的模式种类进行降维。Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000(0次跳变)，00000111(只含一次从0到1的跳变)，10001111(先由1跳到0，再由0跳到1，共两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111(共四次跳变)(这是我的个人理解，不知道对不对)。
　　通过这样的改进，二进制模式的种类大大减少，而不会丢失任何信息。模式数量由原来的2P2P种减少为 P ( P-1)+2种，其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说，二进制模式由原始的256种减少为58种，这使得特征向量的维数更少，并且可以减少高频噪声带来的影响。

2、LBP特征用于检测的原理

　　显而易见的是，上述提取的LBP算子在每个像素点都可以得到一个LBP“编码”，那么，对一幅图像(记录的是每个像素点的灰度值)提取其原始的LBP算子之后，得到的原始LBP特征依然是“一幅图片”(记录的是每个像素点的LBP值)。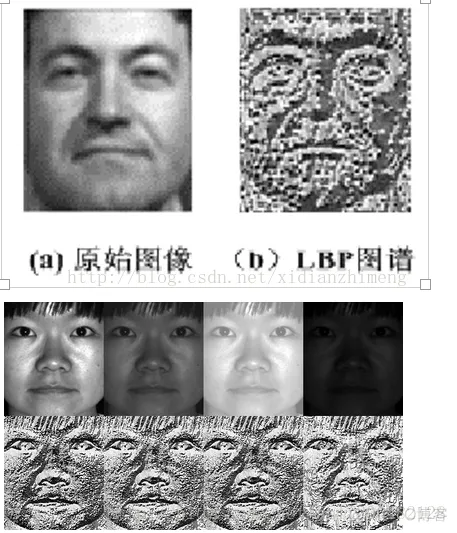【图像识别】基于LBP+LPQ算法融合人脸表情识别matlab源码_matlab_04
　　从上图可以看出LBP对光照具有很强的鲁棒性
　　LBP的应用中，如纹理分类、人脸分析等，一般都不将LBP图谱作为特征向量用于分类识别，而是采用LBP特征谱的统计直方图作为特征向量用于分类识别。
　　因为，从上面的分析我们可以看出，这个“特征”跟位置信息是紧密相关的。直接对两幅图片提取这种“特征”，并进行判别分析的话，会因为“位置没有对准”而产生很大的误差。后来，研究人员发现，可以将一幅图片划分为若干的子区域，对每个子区域内的每个像素点都提取LBP特征，然后，在每个子区域内建立LBP特征的统计直方图。如此一来，每个子区域，就可以用一个统计直方图来进行描述；整个图片就由若干个统计直方图组成；
　　例如：一幅100*100像素大小的图片，划分为10*10=100个子区域(可以通过多种方式来划分区域)，每个子区域的大小为10*10像素；在每个子区域内的每个像素点，提取其LBP特征，然后，建立统计直方图；这样，这幅图片就有10*10个子区域，也就有了10*10个统计直方图，利用这10*10个统计直方图，就可以描述这幅图片了。之后，我们利用各种相似性度量函数，就可以判断两幅图像之间的相似性了；

3、对LBP特征向量进行提取的步骤

　　(1)首先将检测窗口划分为16×16的小区域(cell)；
　　(2)对于每个cell中的一个像素，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数，即得到该窗口中心像素点的LBP值；
　　(3)然后计算每个cell的直方图，即每个数字(假定是十进制数LBP值)出现的频率；然后对该直方图进行归一化处理。
　　(4)最后将得到的每个cell的统计直方图进行连接成为一个特征向量，也就是整幅图的LBP纹理特征向量；
　　然后便可利用SVM或者其他机器学习算法进行分类了。

LPQ(Local Phase Quantization)算法的原理是假设平滑函数h(x)中心对称，则其傅里叶变换为H(u)，对所有H(u)≥0有∠G(u)= ∠F(u),其中F(u)和G(u)分别为原图像和平滑后图像的傅里叶变换，因而在H(u)≥0条件下，图像对平滑有不变性。

为使H(u)≥0，a取为不超过第一个过零点的频率点，其值为a=1/winSize(winSize为输入参数)。分别用f(x)对u1=(a,0),u2=(0,a),u3=(a,a),u4=(a,-a)四个点作STFT，然后分别把四个点的实部和虚部分开,形成一个向量W=[Re{F(u1,x)},Re{F(u2,x)},Re{F(u3,x)},Re{F(u4,x)},Im{F(u1,x)},Im{F(u2,x)},Im{F(u3,x)},Im{F(u4,x)}]T 。

最终得到LPQ变换即为Fx=W*fx。然后对参数进行统计分析，若参数是相关的，则用奇异值分解去相关并且量化。

%日期：2013/7/3
 %首先对jaffe表情图片进行LPB+LPQ特征提取，最后放入支持向量机中分类训练，统计出训练和测试的精度
clc
clear
c=[];
addpath train;
addpath test;
mapping=getmapping(8,'u2');%LBP映射
        W=[2,1,1,1,1,1,2; ...
          2,4,4,1,4,4,2; ...
          1,1,1,0,1,1,1; ...
          0,1,1,0,1,1,0; ...
          0,1,1,1,1,1,0; ...
          0,1,1,2,1,1,0; ...
          0,1,1,1,1,1,0]; 
%提取SU表情的特征
for i=1:20
  B=imread(strcat('train\','SU\',num2str(i),'.tiff'));  %读取SU类别的表情照片
  X = double(B);
  X = imresize(X,[128 128],'bilinear');  %采用'bilinear'：采用双线性插值算法扩展为128*128
  H2=DSLBP(X,mapping,W);%提取图片的LBP直方图
  Gray=X;
  Gray=(Gray-mean(Gray(:)))/std(Gray(:))*20+128;
  lpqhist=lpq(Gray,3,1,1,'nh');       %计算每个照片lpq直方图 
  a=[H2,lpqhist];
  c=[c;a];%LPB和LPQ特征融合
  disp(sprintf('完成SU表情第%i张图片的特征提取',i));
end
%%%以下注释一样
%提取SA表情的特征
for i=1:21     
  B=imread(strcat('train\','SA\',num2str(i),'.tiff'));  
   X = double(B);
  X = imresize(X,[128 128],'bilinear');  %采用'bilinear'：采用双线性插值算法扩展为128*128
  H2=DSLBP(X,mapping,W);%提取图片的LBP直方图
  Gray=X;
  Gray=(Gray-mean(Gray(:)))/std(Gray(:))*20+128;
  lpqhist=lpq(Gray,3,1,1,'nh');       %计算每个照片lpq直方图 
  a=[H2,lpqhist];
  c=[c;a];%LPB和LPQ特征融合
  disp(sprintf('完成SA表情第%i张图片的特征提取',i));
end
%提取NE表情的特征
for i=1:20
  B=imread(strcat('train\','NE\',num2str(i),'.tiff'));
    X = double(B);
  X = imresize(X,[128 128],'bilinear');  %采用'bilinear'：采用双线性插值算法扩展为128*128
  H2=DSLBP(X,mapping,W);%提取图片的LBP直方图
  Gray=X;
  Gray=(Gray-mean(Gray(:)))/std(Gray(:))*20+128;
  lpqhist=lpq(Gray,3,1,1,'nh');       %计算每个照片lpq直方图 
  a=[H2,lpqhist];
  c=[c;a];
  disp(sprintf('完成NE表情第%i张图片的小波特征提取',i));
end
for i=1:22
  B=imread(strcat('train\','HA\',num2str(i),'.tiff'));
   X = double(B);
  X = imresize(X,[128 128],'bilinear');  %采用'bilinear'：采用双线性插值算法扩展为128*128
  H2=DSLBP(X,mapping,W);%提取图片的LBP直方图
  Gray=X;
  Gray=(Gray-mean(Gray(:)))/std(Gray(:))*20+128;
  lpqhist=lpq(Gray,3,1,1,'nh');       %计算每个照片lpq直方图 
  a=[H2,lpqhist];
  c=[c;a];%LPB和LPQ特征融合
  disp(sprintf('完成HA表情第%i张图片的小波特征提取',i));
end
for i=1:22
  B=imread(strcat('train\','FE\',num2str(i),'.tiff'));
    X = double(B);
  X = imresize(X,[128 128],'bilinear');  %采用'bilinear'：采用双线性插值算法扩展为128*128
  H2=DSLBP(X,mapping,W);%提取图片的LBP直方图
  Gray=X;
  Gray=(Gray-mean(Gray(:)))/std(Gray(:))*20+128;
  lpqhist=lpq(Gray,3,1,1,'nh');       %计算每个照片lpq直方图 
  a=[H2,lpqhist];
  c=[c;a];
  disp(sprintf('完成FE表情第%i张图片的小波特征提取',i));
end
for i=1:19
  B=imread(strcat('train\','DI\',num2str(i),'.tiff'));
   X = double(B);
  X = imresize(X,[128 128],'bilinear');  %采用'bilinear'：采用双线性插值算法扩展为128*128
  H2=DSLBP(X,mapping,W);%提取图片的LBP直方图
  Gray=X;
  Gray=(Gray-mean(Gray(:)))/std(Gray(:))*20+128;
  lpqhist=lpq(Gray,3,1,1,'nh');       %计算每个照片lpq直方图 
  a=[H2,lpqhist];
  c=[c;a];
  disp(sprintf('完成DI表情第%i张图片的小波特征提取',i));
end
for i=1:20
  B=imread(strcat('train\','AN\',num2str(i),'.tiff'));
    X = double(B);
  X = imresize(X,[128 128],'bilinear');  %采用'bilinear'：采用双线性插值算法扩展为128*128
  H2=DSLBP(X,mapping,W);%提取图片的LBP直方图
  Gray=X;
  Gray=(Gray-mean(Gray(:)))/std(Gray(:))*20+128;
  lpqhist=lpq(Gray,3,1,1,'nh');       %计算每个照片lpq直方图 
  a=[H2,lpqhist];
  c=[c;a];
  disp(sprintf('完成AN表情第%i张图片的小波特征提取',i));
end
 
d=[];
for i=1:10
  B=imread(strcat('test\','SU\',num2str(i),'.tiff'));
    X = double(B);
  X = imresize(X,[128 128],'bilinear');  %采用'bilinear'：采用双线性插值算法扩展为128*128
  H2=DSLBP(X,mapping,W);%提取图片的LBP直方图
  Gray=X;
  Gray=(Gray-mean(Gray(:)))/std(Gray(:))*20+128;
  lpqhist=lpq(Gray,3,1,1,'nh');       %计算每个照片lpq直方图 
  a=[H2,lpqhist];
  d=[d;a];
  disp(sprintf('完成SU表情测试集第%i张图片的小波特征提取',i));
end
 
verbose = 0;
nbclass=7;
[xsup,w,b,nbsv]=svmmulticlassoneagainstall(P_train,train_label,nbclass,c,lambda,kernel,kerneloption,verbose); %使用支持向量机进行训练获得支持向量
[ypred1,maxi] = svmmultival(P_train,xsup,w,b,nbsv,kernel,kerneloption);  %训练集测试
[ypred2,maxi] = svmmultival(P_test,xsup,w,b,nbsv,kernel,kerneloption);   %测试集测试
CC1=ypred1-train_label;
n1=length(find(CC1==0));
CC2=ypred2-test_label;
n2=length(find(CC2==0));
Accuracytrain=n1/size(train_label,1)   %统计训练精度
Accuracytest=n2/size(test_label,1)     %统计测试精度