​

一、蜉蝣算法

     蜉蝣是属于蜉蝣目的昆虫，是古翅目昆虫的一部分。据估计，全世界有超过3000种蜉蝣。它们的名字来源于它们主要出现在英国的五月。从卵中孵化出来后，肉眼可以看到未成熟的蜉蝣，它们花了几年时间成长为水生若虫，直到它们准备好成年后上升到水面。一只成年蜉蝣只存活几天，直到它完成繁殖的最终目标。为了吸引雌性，大多数雄性成虫成群结队地聚集在水面上几米的地方，通过特有的上下运动模式，表演一场婚礼舞蹈。雌鸟飞入这些蜂群，为了与空中的雄性交配。交配可能只持续几秒钟，当交配完成后，雌鸟将卵落在水面上，它们的生命周期就结束了。

 

【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab
【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_02
​

 1.1 雄性蜉蝣的运动

 

【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_03
【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_02
​

 1.2 雌性蜉蝣的运动

【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_05
【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_02
​

1.3 蜉蝣交配

【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_07
【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_02
​

二、部分代码

%%
clc; clear; close all;
%% Problem Definition
% Objective Function
ANSWER=listdlg('PromptString','Choose Objective Function','SelectionMode','single', 'ListString', {'1. Sphere', '2. Rastrigin'});
if eq(ANSWER,1); ObjectiveFunction=@(x) Sphere(x); funcname='Sphere';
elseif eq(ANSWER,2); ObjectiveFunction=@(x) Rastrigin(x); funcname='Rastrigin';
else; disp('Terminated'); return
end
ProblemSize=[1 50];         % Decision Variables Size
LowerBound=-10;             % Decision Variables Lower Bound
UpperBound= 10;             % Decision Variables Upper Bound
%% Mayfly Parameters
methname='Mayfly Algorithm';
MaxIt=2000;                 % Maximum Number of Iterations
nPop=20; nPopf=20;          % Population Size (males and females)
g=0.8;                      % Inertia Weight
gdamp=1;                    % Inertia Weight Damping Ratio
a1=1.0;                     % Personal Learning Coefficient
a2=1.5; a3=1.5;             % Global Learning Coefficient
beta=2;                     % Distance sight Coefficient
dance=5;                    % Nuptial Dance
fl=1;                       % Random flight
dance_damp=0.8;             % Damping Ratio
fl_damp=0.99;
% Mating Parameters
nc=20;                      % Number of Offsprings (also Parnets)
nm=round(0.05*nPop);        % Number of Mutants
mu=0.01;                    % Mutation Rate
% Velocity Limits
VelMax=0.1*(UpperBound-LowerBound); VelMin=-VelMax;
%% Initialization
empty_mayfly.Position=[];
empty_mayfly.Cost=[];
empty_mayfly.Velocity=[];
empty_mayfly.Best.Position=[];
empty_mayfly.Best.Cost=[];
Mayfly=repmat(empty_mayfly,nPop,1);   % Males
Mayflyf=repmat(empty_mayfly,nPopf,1); % Females
GlobalBest.Cost=inf;
funccount=0;
for i=1:nPop
    % Initialize Position of Males
    Mayfly(i).Position=unifrnd(LowerBound,UpperBound,ProblemSize);
    % Initialize Velocity
    Mayfly(i).Velocity=zeros(ProblemSize);
    % Evaluation
    Mayfly(i).Cost=ObjectiveFunction(Mayfly(i).Position);
    % Update Personal Best
    Mayfly(i).Best.Position=Mayfly(i).Position;
    Mayfly(i).Best.Cost=Mayfly(i).Cost;
    funccount=funccount+1;
    % Update Global Best
    if Mayfly(i).Best.Cost<GlobalBest.Cost
        GlobalBest=Mayfly(i).Best;
    end
end
for i=1:nPopf
    % Initialize Position of Females
    Mayflyf(i).Position=unifrnd(LowerBound,UpperBound,ProblemSize);
    Mayflyf(i).Velocity=zeros(ProblemSize);
    Mayflyf(i).Cost=ObjectiveFunction(Mayflyf(i).Position);
    funccount=funccount+1;
    % Update Global Best (Uncomment if you use the PGB-IMA version)
    %if Mayflyf(i).Best.Cost<GlobalBest.Cost
    %    GlobalBest=Mayflyf(i).Best;
    %end
end
BestSolution=zeros(MaxIt,1);
%% Mayfly Main Loop
for it=1:MaxIt
    for i=1:nPopf
        % Update Females
        e=unifrnd(-1,+1,ProblemSize);
        rmf=(Mayfly(i).Position-Mayflyf(i).Position);
        if Mayflyf(i).Cost>Mayfly(i).Cost
            Mayflyf(i).Velocity = g*Mayflyf(i).Velocity ...
                +a3*exp(-beta.*rmf.^2).*(Mayfly(i).Position-Mayflyf(i).Position);
        else
            Mayflyf(i).Velocity = g*Mayflyf(i).Velocity+fl*(e);
        end
        % Apply Velocity Limits
        Mayflyf(i).Velocity = max(Mayflyf(i).Velocity,VelMin);
        Mayflyf(i).Velocity = min(Mayflyf(i).Velocity,VelMax);
        % Update Position
       c/2,2);
    for k=1:nc/2
        % Select Parents
        i1=k;
        i2=k;
        p1=Mayfly(i1);
        p2=Mayflyf(i2);
        % Apply Crossover
        [MayflyOffspring(k,1).Position, MayflyOffspring(k,2).Position]=Crossover(p1.Position,p2.Position,LowerBound,UpperBound);
        % Evaluate Offsprings
        MayflyOffspring(k,1).Cost=ObjectiveFunction(MayflyOffspring(k,1).Position);
        if MayflyOffspring(k,1).Cost<GlobalBest.Cost
            GlobalBest=MayflyOffspring(k,1);
        end
        funccount=funccount+1;
        MayflyOffspring(k,2).Cost=ObjectiveFunction(MayflyOffspring(k,2).Position);
        if MayflyOffspring(k,2).Cost<GlobalBest.Cost
            GlobalBest=MayflyOffspring(k,2);
        end
        funccount=funccount+1;
        MayflyOffspring(k,1).Best.Position = MayflyOffspring(k,1).Position;
        MayflyOffspring(k,1).Best.Cost = MayflyOffspring(k,1).Cost;
        MayflyOffspring(k,1).Velocity= zeros(ProblemSize);
        MayflyOffspring(k,2).Best.Position = MayflyOffspring(k,2).Position;
        MayflyOffspring(k,2).Best.Cost = MayflyOffspring(k,2).Cost;
        MayflyOffspring(k,2).Velocity= zeros(ProblemSize);
    end
    MayflyOffspring=MayflyOffspring(:);
    % Mutation
    MutMayflies=repmat(empty_mayfly,nm,1);
    for k=1:nm
        % Select Parent
        i=randi([1 nPop]);
        p=MayflyOffspring(i);
        %p=Mayfly(i);
        MutMayflies(k).Position=Mutate(p.Position,mu,LowerBound,UpperBound);
        % Evaluate Mutant
        MutMayflies(k).Cost=ObjectiveFunction(MutMayflies(k).Position);
  
    [~, SortMayflies]=sort([Mayfly.Cost]);
    Mayfly=Mayfly(SortMayflies);
    Mayfly=Mayfly(1:nPop); % Keep best males
    [~, SortMayflies]=sort([Mayflyf.Cost]);
    Mayflyf=Mayflyf(SortMayflies);
    Mayflyf=Mayflyf(1:nPopf); % Keep best females
    BestSolution(it)=GlobalBest.Cost;
    disp([methname ' on the ' funcname  ' Function: Iteration = ' num2str(it)  ', ' funcname ', Evaluations = ' num2str(funccount)  '. Best Cost = ' num2str(BestSolution(it))]);
    g=g*gdamp;
    dance = dance*dance_damp;
    fl = fl*fl_damp;
end
%% Results
figure;
plot(BestSolution,'LineWidth',2); semilogy(BestSolution,'LineWidth',2);
xlabel('Iterations'); ylabel('Objective function'); grid on;
%%
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.
  • 16.
  • 17.
  • 18.
  • 19.
  • 20.
  • 21.
  • 22.
  • 23.
  • 24.
  • 25.
  • 26.
  • 27.
  • 28.
  • 29.
  • 30.
  • 31.
  • 32.
  • 33.
  • 34.
  • 35.
  • 36.
  • 37.
  • 38.
  • 39.
  • 40.
  • 41.
  • 42.
  • 43.
  • 44.
  • 45.
  • 46.
  • 47.
  • 48.
  • 49.
  • 50.
  • 51.
  • 52.
  • 53.
  • 54.
  • 55.
  • 56.
  • 57.
  • 58.
  • 59.
  • 60.
  • 61.
  • 62.
  • 63.
  • 64.
  • 65.
  • 66.
  • 67.
  • 68.
  • 69.
  • 70.
  • 71.
  • 72.
  • 73.
  • 74.
  • 75.
  • 76.
  • 77.
  • 78.
  • 79.
  • 80.
  • 81.
  • 82.
  • 83.
  • 84.
  • 85.
  • 86.
  • 87.
  • 88.
  • 89.
  • 90.
  • 91.
  • 92.
  • 93.
  • 94.
  • 95.
  • 96.
  • 97.
  • 98.
  • 99.
  • 100.
  • 101.
  • 102.
  • 103.
  • 104.
  • 105.
  • 106.
  • 107.
  • 108.
  • 109.
  • 110.
  • 111.
  • 112.
  • 113.
  • 114.
  • 115.
  • 116.
  • 117.
  • 118.
  • 119.
  • 120.
  • 121.
  • 122.
  • 123.
  • 124.
  • 125.
  • 126.
  • 127.
  • 128.
  • 129.
  • 130.
  • 131.
  • 132.
  • 133.
  • 134.
  • 135.
  • 136.
  • 137.
  • 138.
  • 139.
  • 140.
  • 141.
  • 142.
【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_02

三、仿真结果

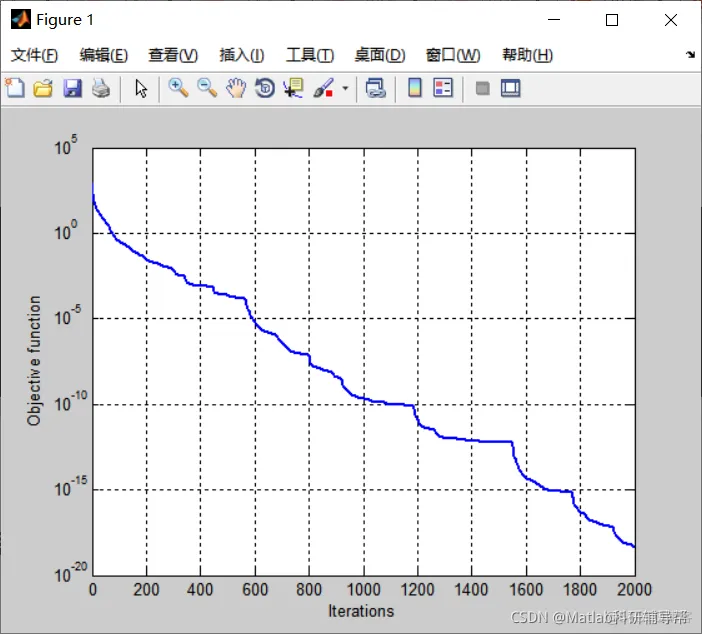
【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_10
【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_02
​

四、参考文献

Zervoudakis, K., & Tsafarakis, S. (2020). A mayfly optimization algorithm. Computers & Industrial Engineering, 145, 106559. https://doi.org/10.1016/j.cie.2020.106559

【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_12
【优化求解-单目标求解】基于蜉蝣算法求解单目标问题matlab源码_matlab_02
​

​