随机模型预测控制（SMPC）——考虑概率约束（Matlab代码实现）

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

​

💥1 概述

随机模型预测控制（SMPC）中考虑概率约束的研究

模型预测控制（MPC）又称为滚动时域控制和滚动时域控制，是一种强有力的工程应用技术。MPC的价值主要体现在其处理约束的内在能力，同时最小化一些代价（或最大化一些回报）。MPC的基本思想是用有限时域最优控制问题来反复逼近无限时域约束最优控制问题。在每一个时间步，这样一个有限时域问题被解决，并且只有第一个输入以一种后退时域的方式被应用到系统中。

MPC使用一个对象模型来预测其未来的行为，然后根据预测计算出一个最优的输入轨迹。然而，在大多数实际应用中，由于模型的不确定性或外界干扰，都无法得到精确的模型。在文献中，不确定性通常是通过描述一个鲁棒MPC问题来解决的，在这个问题中，不确定性被假定为有界的，并且计算出满足每个可能的不确定性实现的约束的控制律。这种悲观的观点可能会显著降低控制器的整体性能，因为需要防范低概率不确定性异常值。

随机MPC（SMPC）提供了另一种对不确定性不那么悲观的观点。在SMPC中，约束是概率解释的，允许很小的违反概率。在这种情况下，甚至可以研究无界不确定性。不幸的是，SMPC问题通常很难解决，只能近似地或通过施加特定的问题结构来解决。在这种情况下，我们主要关注以下问题：但是如果不确定性没有界，会发生什么？或者当它不是均匀分布的时候？一个不太保守的方法显然是考虑到这些可能性，确定不确定性的适当分布，并制定一个随机的MPC问题。

一、SMPC与概率约束的核心概念

随机模型预测控制（SMPC）通过引入概率约束，将传统模型预测控制（MPC）中的硬约束转化为软约束，允许系统在特定概率下违反约束，从而平衡控制性能与鲁棒性。其核心思想在于：

1. 不确定性建模：将系统扰动（如风速变化、人类行为不确定性）建模为随机变量，并假设其服从特定概率分布（如高斯分布）。
2. 概率约束转化：通过数学工具（如Chebyshev-Cantelli不等式、凸近似）将概率约束转化为确定性约束，降低计算复杂度。
3. 优化问题重构：将原随机优化问题转化为凸二次规划或二阶锥规划（SOCP），利用高效求解器实现实时控制。

典型应用场景：

• 风电系统：处理风速预测的不确定性，优化双馈感应发电机（DFIG）的能量捕获。
• 自动驾驶：应对目标车辆行为的随机性，提升路径规划的安全性。
• 人机交互：降低人类行为不确定性对机器人控制的影响，例如模拟驾驶场景中的碰撞率。

二、概率约束的转化方法与优势

1. Chebyshev-Cantelli不等式法
   • 原理：利用噪声的一阶矩（均值）和二阶矩（方差），将状态和输入的概率约束转化为确定性形式。
   • 优势：无需精确知道扰动分布，仅需假设其有界或满足特定矩条件，适用于部分状态观测系统。
   • 案例：在基于观测器的SMPC中，通过引入附加摄动量，最大化初始可行域并计算控制律，验证了算法的递推可行性。
2. 凸近似与场景法
   • 原理：生成一系列扰动场景近似概率分布，将随机优化问题转化为确定性约束优化问题。
   • 优势：避免对扰动分布的精确假设，降低计算复杂度；通过调整场景数量平衡控制性能与计算负担。
   • 案例：在加性扰动线性系统中，通过场景法处理机会约束，允许一定程度的约束违反，提升系统鲁棒性。
3. 联合机会约束（JCC）
   • 原理：对状态变量施加联合概率约束，确保所有约束同时满足的概率不低于阈值。
   • 优势：适用于多状态约束系统，如化工过程中的温度、压力联合控制。
   • 案例：在连续丙酮-丁醇-乙醇发酵过程中，通过JCC-SMPC实现高附加值生物燃料的稳定生产。

三、SMPC与鲁棒MPC（RMPC）的对比

特性	SMPC	RMPC
不确定性处理	允许无界扰动，通过概率约束放松控制	假设扰动有界，采用最坏情况优化
计算复杂度	较低（凸近似/场景法）	较高（需处理所有可能扰动实现）
控制性能	平衡性能与鲁棒性，适应低概率异常值	保守性强，可能降低整体性能
适用场景	风电、自动驾驶、人机交互等	电力电子、飞行器等高可靠性要求领域

关键结论：

• SMPC通过概率约束放松了RMPC的保守性，尤其适用于扰动分布未知或无界的情况。
• RMPC在需要严格满足所有约束的场景中仍具优势，如核电站控制。

四、前沿研究方向与挑战

1. 高效求解算法
   • 挑战：SMPC的优化问题通常为非凸，求解效率低。
   • 进展：基于情景的凸近似方法、分布式优化技术（如ADMM）可显著提升计算速度。
2. 长时域性能保障
   • 挑战：滚动时域控制可能导致累积误差，影响长期稳定性。
   • 进展：通过引入终端约束、Lyapunov函数等方法，建立闭环系统的随机稳定性条件。
3. 数据驱动的SMPC
   • 挑战：传统SMPC依赖精确模型，但实际系统常存在模型误差。
   • 进展：结合机器学习（如高斯过程回归）构建数据驱动的扰动模型，提升适应性。

📚2 运行结果

​

​

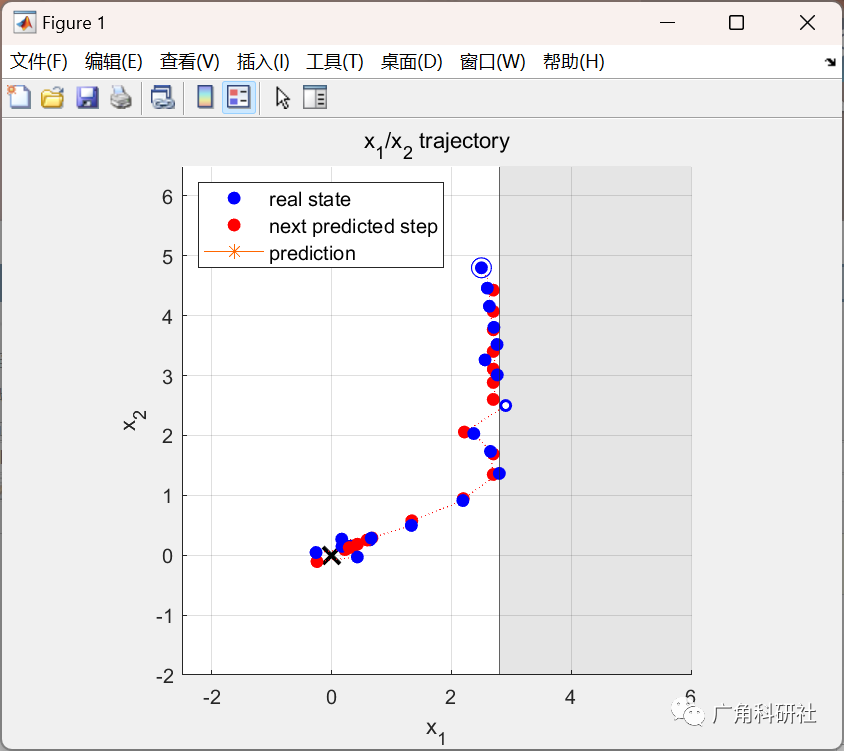
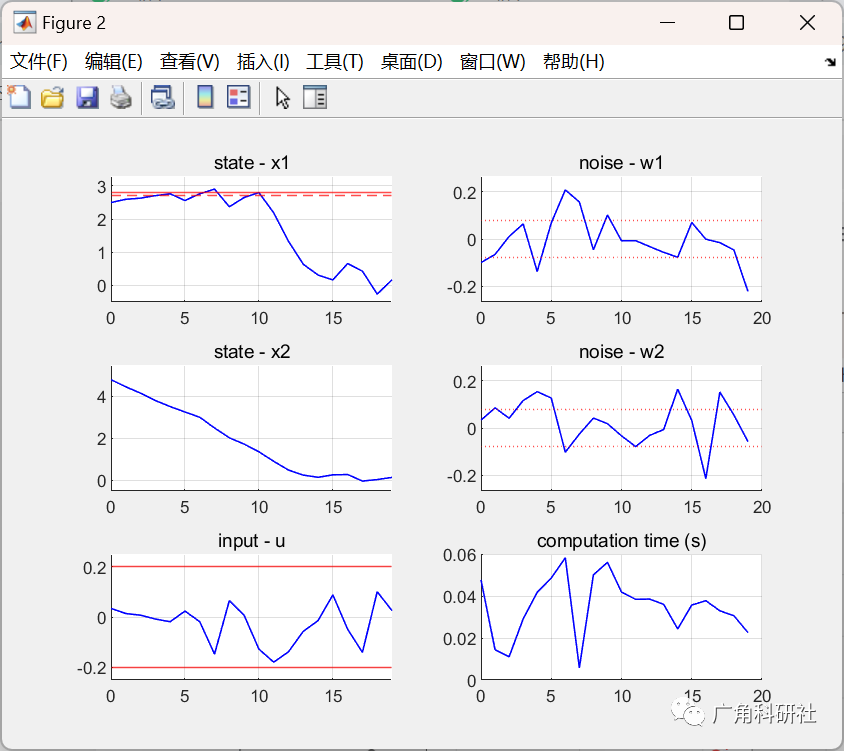
主函数部分代码：

% plot inputs and states 
​
%% run smpc (runs new MPC simulation)
[x,u, x1_limit, sig, beta, s, comp_time]= run_mpc;
​
​
​
%% plot input and states
​
% set up figure for input and states
figure(2)
clf
​
plot_noise = 1;         % plot noise? 0: no; 1: yes (if yes: computation time will also be plotted)
% if noise was not saved, automatically swich to 0
if exist('s','var') == 0
    plot_noise = 0;
end
​
​
steps = 0:length(x)-1;  % get steps (last input is computed but not applied) 
​
​
% state x1
if plot_noise == 0
    subplot(3,1,1)
else
    subplot(3,2,1)
end
hold on
title('state - x1')
grid on
plot(steps,x(:,1), 'b', 'Linewidth',0.8)
% plot constraint only if close enough
if x1_limit < 40
    yline(x1_limit, 'r', 'Linewidth',0.8)
    ylim([-0.5 x1_limit+0.5]);
    gamma1 = sqrt(2*[1;0]'*[sig^2 0; 0 sig^2]*[1;0])*erfinv(2*beta-1); % chance constraint addition for first predicted step
    yline(x1_limit-gamma1, 'r--', 'Linewidth',0.8)
end
xlim([steps(1) steps(end)]);
hold off
​
​
% state x2
if plot_noise == 0
    subplot(3,1,2)
else
    subplot(3,2,3)
end
hold on
title('state - x2')
plot(steps,x(:,2), 'b', 'Linewidth',0.8)
grid on
ylim([-0.5 5.5]);
xlim([steps(1) steps(end)]);
hold off
​
​
% input u
if plot_noise == 0
    subplot(3,1,3)
else
    subplot(3,2,5)
end
K = [0.2858 -0.4910];
u_applied = [];
for i = 1:length(u)
    u_applied(i,1) = u(i,1) - K*[x(i,1); x(i,2)];
end
hold on
title('input - u')
grid on
plot(steps,u_applied(:,1), 'b', 'Linewidth',0.8)
yline(0.2,'r', 'Linewidth',0.8)
yline(-0.2,'r', 'Linewidth',0.8)
ylim([-0.25 0.25]);
xlim([steps(1) steps(end)]);
hold off
​
​
% plot noise (given seeding)
% rng(30,'twister'); % hardcoded seeding
rng(s);             % retrieve seeding from run_mpc
​
w = [];
​
for i = 1: length(x)
    w(i,1) = normrnd(0,sig);
    w(i,2) = normrnd(0,sig);
end
​
% plot subplots with noise
if plot_noise == 1
    
    w_max = max(max(abs(w))); % get largest uncertainty  
        
    
    subplot(3,2,2)
    hold on
    title('noise - w1')
    plot(steps, w(:,1), 'b', 'Linewidth',0.8)
    % plot standard deviation
    yline(sig,'r:', 'Linewidth',0.8)
    yline(-sig,'r:', 'Linewidth',0.8)
    if w_max > 0
        ylim([-1.2*w_max 1.2*w_max])
    end
​

🎉3 参考文献

[1]T. Br¨udigam, M. Olbrich, M. Leibold, and D. Wollherr. Combining stochastic and scenario model predictive control to handle target vehicle uncertainty in autonomous driving. In 21st IEEE International Conference on Intelligent Transportation Systems, Maui, USA, 2018.​

部分理论引用网络文献，若有侵权联系博主删除。

🌈4 Matlab代码实现