（优化算法）浮力优化算法（Matlab实现）

原创已于 2024-10-27 20:47:58 修改 · 441 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2024-10-27 20:38:41 首次发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

浮力优化算法（Buoyancy Optimization Algorithm，BOA）是一种受自然界中浮力现象启发而提出的新型优化算法。该算法的核心思想是模拟物体在液体中受到浮力作用的运动过程来进行优化搜索。在优化问题中，每个解被看作是一个在虚拟“液体”中的“物体”。这些“物体”根据其适应度值（类似于物体的密度）以及与最优解的相对位置来确定所受到的浮力大小和方向。浮力优化算法通常具有以下特点： 1. 全局搜索能力：通过模拟浮力的随机作用，算法能够在搜索空间中进行广泛的探索，有助于找到全局最优解。 2. 局部搜索能力：随着搜索的进行，算法可以逐渐聚焦于有潜力的区域，进行精细的局部搜索，提高解的精度。 3. 自适应性：算法能够根据搜索进程和当前解的状态动态调整搜索策略，适应不同类型的优化问题。 4. 灵活性：可以应用于多种类型的优化问题，如函数优化、组合优化、工程设计优化等。在实际应用中，浮力优化算法可以用于解决各种复杂的优化问题，例如优化神经网络的权重、寻找最优的生产调度方案、设计最优的工程结构等。它为解决复杂优化问题提供了一种新的思路和方法，具有一定的理论价值和实际应用前景。

📚2 运行结果

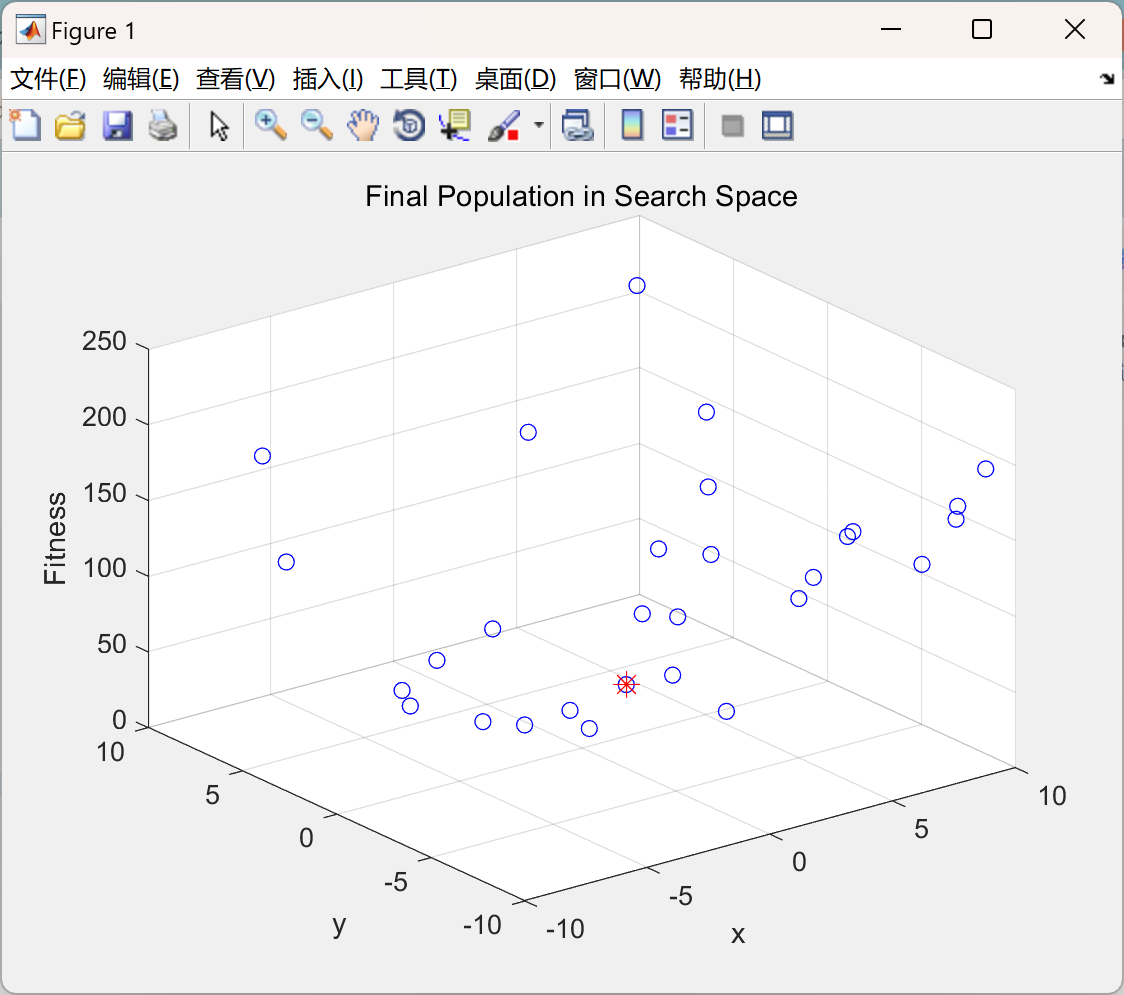
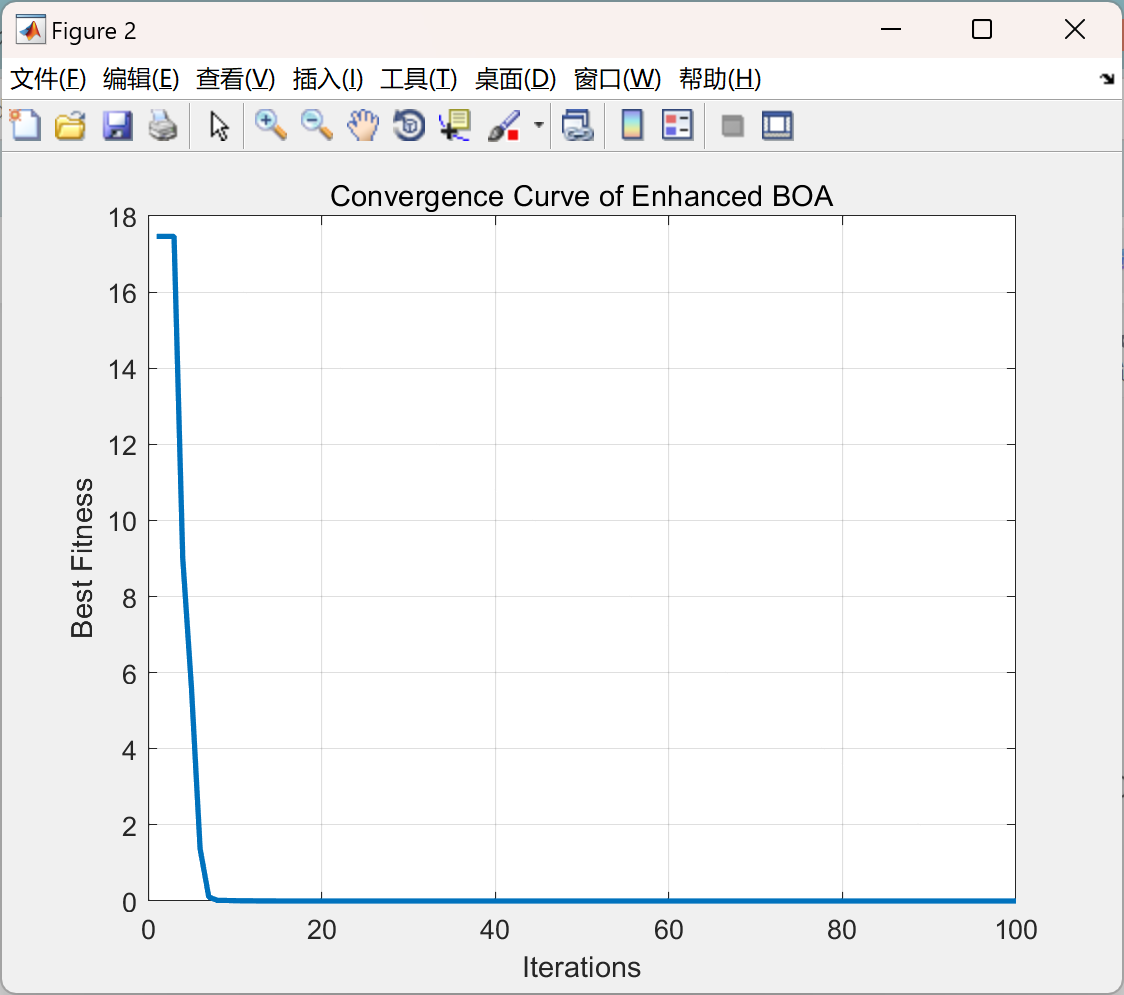
部分函数代码：

function [bestSolution, bestFitness] = enhancedBuoyancyOptimizationAlgorithm(maxIterations, initialPopulationSize,minPopulationSize, lowerBound, upperBound)
    % Enhanced Buoyancy Optimization Algorithm (BOA)
    %
    % Parameters:
    %   maxIterations: Maximum number of iterations
    %   initialPopulationSize: Initial size of the population
    %   minPopulationSize: Minimum population size after dynamic adjustment
    %   lowerBound, upperBound: Bounds of the search space
    
    % Problem Dimension
    dimension = 3; % Modify as needed
    
    % Initialize population
    populationSize = initialPopulationSize;
    population = lowerBound + (upperBound - lowerBound) * rand(populationSize, dimension);
    fitness = arrayfun(@(idx) objectiveFunction(population(idx, :)), 1:populationSize);
    
    % Set the initial best solution
    [bestFitness, bestIdx] = min(fitness);
    bestSolution = population(bestIdx, :);

    % Initialize variables to store best fitness history for plotting
    bestFitnessHistory = zeros(maxIterations, 1);

    % Optimization loop
    for iter = 1:maxIterations
        inertiaWeight = 0.9 - iter * (0.9 - 0.4) / maxIterations; % Adaptive inertia weight
        
        for i = 1:populationSize
            % Calculate distance to best solution
            distanceToBest = norm(bestSolution - population(i, :));
            
            % Adaptive Buoyancy Force
            buoyancyForceMagnitude = exp(-distanceToBest / (iter + 1));
            buoyancyForce = inertiaWeight * buoyancyForceMagnitude * (bestSolution - population(i, :));
            
            % Random Perturbation for Exploration
            explorationFactor = 0.1 * (upperBound - lowerBound) * randn(1, dimension);
            if rand < 0.2 % Apply perturbation with a probability
                buoyancyForce = buoyancyForce + explorationFactor;
            end
            
            % Update position based on buoyancy force
            population(i, :) = population(i, :) + buoyancyForce;
            
            % Boundary Handling
            population(i, :) = max(min(population(i, :), upperBound), lowerBound);
            
            % Evaluate fitness
            newFitness = objectiveFunction(population(i, :));
            if newFitness < fitness(i)
                fitness(i) = newFitness;